МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра биотехнических систем

отчет

по лабораторной работе №3

по дисциплине «Методы обработки и анализа биомедицинских сигналов и данных»

Тема: КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ЭЭГ

Вариант 7

Студентки гр. 7501		Сачкова Н. Д.
		Кирьянова А. М.
Преподаватель		Калиниченко А. Н.

Санкт-Петербург

2019

Цель работы: ознакомление с использованием корреляционных функций для исследования ЭЭГ.

Основные теоретические положения

При анализе медико-биологических сигналов часто используются автокорреляционная функция (АКФ) и взаимная корреляционная функция (ВКФ), которые соответственно задаются выражениями:

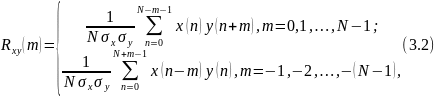
где x(n) и y(n) – отсчеты двух сигналов, N – число отсчетов для каждого из них, m – число сдвигов, а σ_x и σ_y – среднеквадратичные отклонения.

Значения функций, рассчитанных по формулам (3.1) и (3.2), лежат в пределах от ‑1 до +1. АКФ показывает наличие внутренних периодичностей в сигнале. Она всегда равна единице при нулевом сдвиге (т. е. при m = 0), симметрична относительно оси ординат и затухает с увеличением m тем медленнее, чем сильнее выражены периодичности в сигнале.

ВКФ позволяет оценить наличие сходных по частоте колебаний в двух сигналах. Если при каких-то величинах сдвига модуль значения ВКФ приближается к единице, то это является признаком наличия в сигналах однотипных изменений, происходящих с задержкой, равной сдвигу.

АКФ и ВКФ широко используются при анализе электроэнцефалограмм (ЭЭГ). АКФ позволяет выявить присутствие ритмов в ЭЭГ, а ВКФ дает возможность оценить взаимосвязь электроэнцефалографических событий в сигналах ЭЭГ, снятых в разных зонах на поверхности головы.

Практическая часть

Исходные данные:

Вариант	Fd, Гц	tmax, c	A1	F1, Гц	A2	F2, Гц	Имя файла ЭЭГ
7	350	0,8	25	9	10	5	R3_07.txt

Задание 1: Исследование характера изменения АКФ и ВКФ для трех тестовых сигналов: двух синусоид с разными частотами и суммы этих двух синусоид. Построение графиков сигналов и всех рассчитанных функций.

Код программы:

%тестовые сигналы

clc;

clear all;

close all;

X0=50;

Y0=80;

W0=1200;

H0=600;

x1=50;

y1=430;

w1=200;

h1=150;

dy=30;

dx=20;

w2=40;

h2=10;

figure('Color','[1 1 1]','Position',[X0,Y0,W0,H0]);

hAxes11=axes('Units','pixels','Position',[x1,y1,w1,h1]);

hAxes21=axes('Units','pixels','Position',[x1,y1-h1-dy,w1,h1]);

hAxes31=axes('Units','pixels','Position',[x1,y1-2*h1-2*dy,w1,h1]);

hAxes12=axes('Units','pixels','Position',[x1+w1+dx,y1,2*w1,h1]);

hAxes22=axes('Units','pixels','Position',[x1+w1+dx,y1-h1-dy,2*w1,h1]);

hAxes32=axes('Units','pixels','Position',[x1+w1+dx,y1-2*h1-2*dy,2*w1,h1]);

hAxes13=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1,2*w1,h1]);

hAxes23=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1-h1-dy,2*w1,h1]);

hAxes33=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1-2*h1-2*dy,2*w1,h1]);

%параметры сигнала

A1=25;

A2=10;

F1=9;

F2=5;

Fs=350;

tmax=0.8;

T=1/Fs;

t=0:T:tmax-T;

S1=A1*sin(2*pi*F1*t);

S2=A2*sin(2*pi*F2*t);

S3=S1+S2;

axes(hAxes11);

plot(t,S1);

grid minor;

axes(hAxes21);

plot(t,S2);

grid minor;

axes(hAxes31);

plot(t,S3);

grid minor;

%OY

Asum=A1+A2;

set(hAxes11,'Ylim',[-Asum Asum]);

hold on;

set(hAxes21,'Ylim',[-Asum Asum]);

hold on;

set(hAxes31,'Ylim',[-Asum Asum]);

hold on;

%АКФ

tcf=-tmax+T:T:tmax-T;

acf1=xcorr(S1,'coeff');

axes(hAxes12);

set(hAxes12,'Ylim',[-1 1]);

hold on;

plot(tcf,acf1);

grid minor;

acf2=xcorr(S2,'coeff');

axes(hAxes22);

set(hAxes22,'Ylim',[-1 1]);

hold on;

plot(tcf,acf2);

grid minor;

acf3=xcorr(S3,'coeff');

axes(hAxes32);

set(hAxes32,'Ylim',[-1 1]);

hold on;

plot(tcf,acf3);

grid minor;

%ВКФ

ccf13=xcorr(S1,S3,'coeff');

axes(hAxes13);

ylim([-1 1]);

hold on;

plot(tcf,ccf13);

grid minor;

ccf23=xcorr(S2,S3,'coeff');

axes(hAxes23);

ylim([-1 1]);

hold on;

plot(tcf,ccf23);

grid minor;

ccf31=xcorr(S3,S1,'coeff');

axes(hAxes33);

ylim([-1 1]);

hold on;

plot(tcf,ccf31);

grid minor;

Полученный в результате программы график: Рис. 1.:

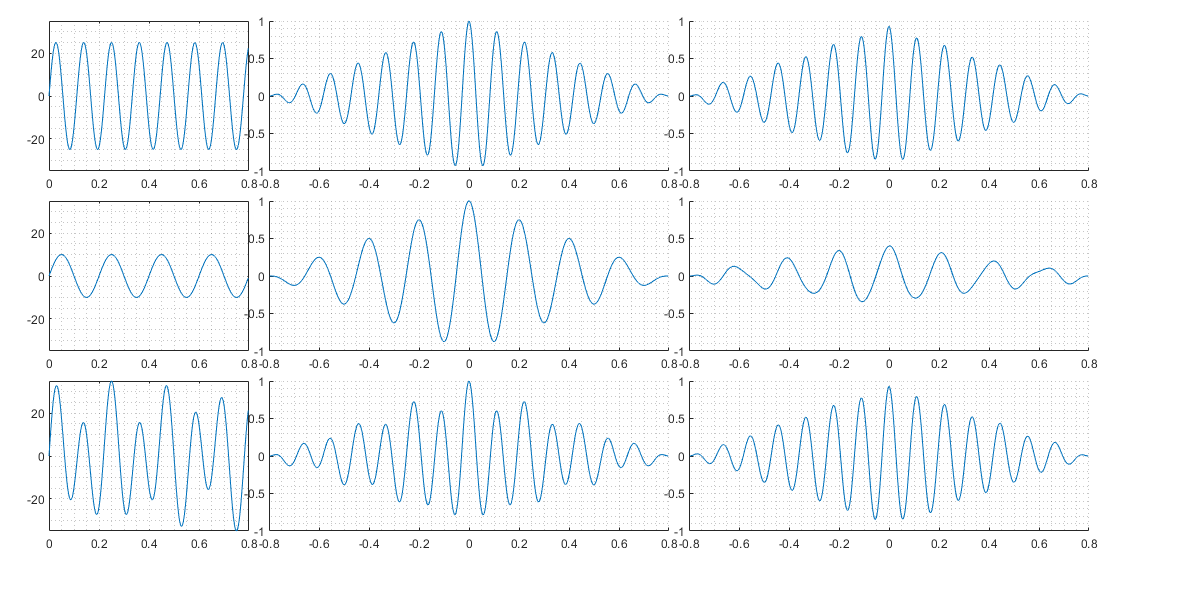
Рис. 1. АКФ ВКФ для тестовых синусоид

Задание 2: выполнение расчет АКФ и ВКФ для трех фрагментов реальной ЭЭГ. Построение графики сигналов и всех рассчитанных функций.

Код программы:

%eeg

clc;

clear all;

close all;

X0=50;

Y0=80;

W0=1200;

H0=600;

x1=50;

y1=430;

w1=200;

h1=150;

dy=30;

dx=20;

w2=40;

h2=10;

figure('Color','[1 1 1]','Position',[X0,Y0,W0,H0]);

hAxes11=axes('Units','pixels','Position',[x1,y1,w1,h1]);

hAxes21=axes('Units','pixels','Position',[x1,y1-h1-dy,w1,h1]);

hAxes31=axes('Units','pixels','Position',[x1,y1-2*h1-2*dy,w1,h1]);

hAxes12=axes('Units','pixels','Position',[x1+w1+dx,y1,2*w1,h1]);

hAxes22=axes('Units','pixels','Position',[x1+w1+dx,y1-h1-dy,2*w1,h1]);

hAxes32=axes('Units','pixels','Position',[x1+w1+dx,y1-2*h1-2*dy,2*w1,h1]);

hAxes13=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1,2*w1,h1]);

hAxes23=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1-h1-dy,2*w1,h1]);

hAxes33=axes('Units','pixels','Position',[x1+3*w1+2*dx,y1-2*h1-2*dy,2*w1,h1]);

%параметры сигнала

Fs=250;

S=load('R3_07.txt');

N=length(S);

S1=S(1:N,1);

S2=S(1:N,2);

S3=S(1:N,3);

T=1/Fs;

tmax=N*T;

t=0:T:tmax-T;

%пределы

Amax(1)=max(S1);

Amax(2)=max(S2);

Amax(3)=max(S3);

Amin(1)=min(S1);

Amin(2)=min(S2);

Amin(3)=min(S3);

%графики

axes(hAxes11);

plot(t,S1);

grid minor;

ylim([min(Amin) max(Amax)]);

hold on;

axes(hAxes21);

plot(t,S2);

grid minor;

ylim([min(Amin) max(Amax)]);

hold on;

axes(hAxes31);

plot(t,S3);

grid minor;

ylim([min(Amin) max(Amax)]);

hold on;

%АКФ

tcf=-tmax+T:T:tmax-T;

acf1=xcorr(S1,'coeff');

axes(hAxes12);

hold on;

plot(tcf,acf1);

grid minor;

%ylim([min(Amin) max(Amax)]);

hold on;

acf2=xcorr(S2,'coeff');

axes(hAxes22);

hold on;

plot(tcf,acf2);

grid minor;

%ylim([min(Amin) max(Amax)]);

hold on;

acf3=xcorr(S3,'coeff');

axes(hAxes32);

hold on;

plot(tcf,acf3);

grid minor;

%ylim([min(Amin) max(Amax)]);

hold on;

%ВКФ

ccf13=xcorr(S1,S2,'coeff');

axes(hAxes13);

hold on;

plot(tcf,ccf13);

grid minor;

hold on;

ccf23=xcorr(S2,S3,'coeff');

axes(hAxes23);

hold on;

plot(tcf,ccf23);

grid minor;

hold on;

ccf31=xcorr(S3,S1,'coeff');

axes(hAxes33);

hold on;

plot(tcf,ccf31);

grid minor;

hold on;

Полученный в результате программы график: Рис. 2.:

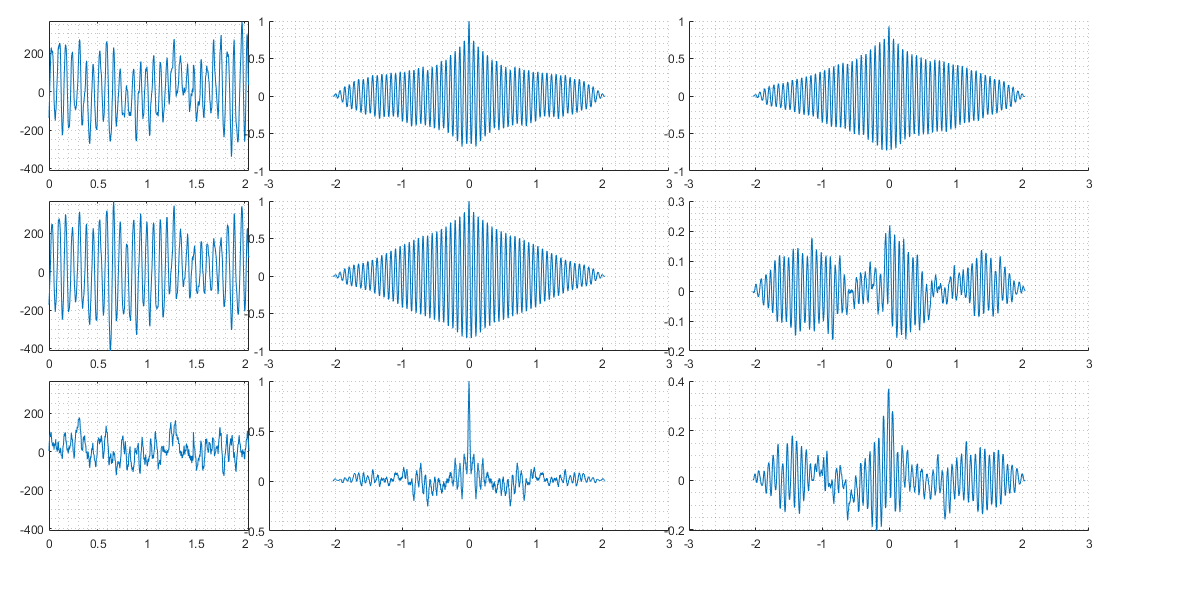
Рис. 2. АКФ ВКФ для реальных записей ЭЭГ

Выводы:

1. АКФ показывает наличие внутренних периодичностей в сигнале, Геометрический смысл автокорреляционной функции заключается в определении площади пересечения функции и её копии, сдвинутой во времени.

ВКФ определяет временную связь двух сигналов во времени. Если сигналы не зависимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом.

2. Отличие «нормированной» и «ненормированной» оценок АКФ. АКФ задается через функцию xcorr, которая по умолчанию является ненормированной, чтобы АКФ стала нормированной, нужно добавить входной параметр coeff.

3. Отличие «смещенной» и «несмещенной» оценок АКФ в том, что несмещенная имеет перед собой коэффициент .

4. В работе для вычисления АКФ и ВКФ используют следующие функции пакет MATLAB:

АКФ: acf=xcorr(s,'coeff');

ВКФ: ccfij=xcorr(si,sj,'coeff').

5. Графики АКФ и ВКФ сходятся к нулю по краям, так как сигналы выходят из 0 и при корреляции сохранят по краям это значение.

6. По заданию поля для графиков требуется сделать шире вдвое, так как размер получаемого в результате вектора вдвое больше, чем размер вектора сигнала, значит для вывода графика необходимо создать соответствующий вектор значений аргумента

7. На графике АКФ наблюдается симметрия относительно 0, потому что функция четная. (Значение автокорреляционной функции в нуле периодического сигнала равно средней мощности сигнала)

8. О характере исходных сигналов по виду полученных АКФ и ВКФ можно судить по их длительности, которая называется интервалом корреляции. Он определяется как отношение площади, ограниченной АКФ сигнала, к энергии сигнала. Если модуль времени сигнала больше интервала корреляции, то значения не коррелированы.