МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра БТС
отчет
по лабораторной работе №7
по дисциплине «МОиАБМСиД»
Тема: Расчет корреляционной матрицы ЭЭГ
Вариант 4
Студенты гр. 7501 |
|
Исаков А.О. |
|
|
Фалевская А. |
Преподаватель |
|
Ровша М.В. |
Санкт-Петербург
2020
Цель работы: исследование взаимосвязи каналов ЭЭГ с использованием коэффициента взаимной корреляции.
Основные теоретические положения.
Коэффициент
взаимной корреляции (КВК) является
максимумом ВКФ функции при сдвиге
:
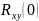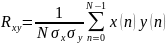
где x(n)
и y(n)
– отсчеты двух дискретных сигналов, N
– число отсчетов
для каждого из сигналов, а
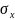и
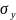– среднеквадратичные отклонения
сигналов.
В общем виде функция взаимной корреляции между двумя функциями имеет форму:
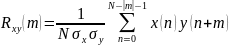
где m
– величина временного сдвига, величина
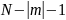определяет область пересечения двух
функций.
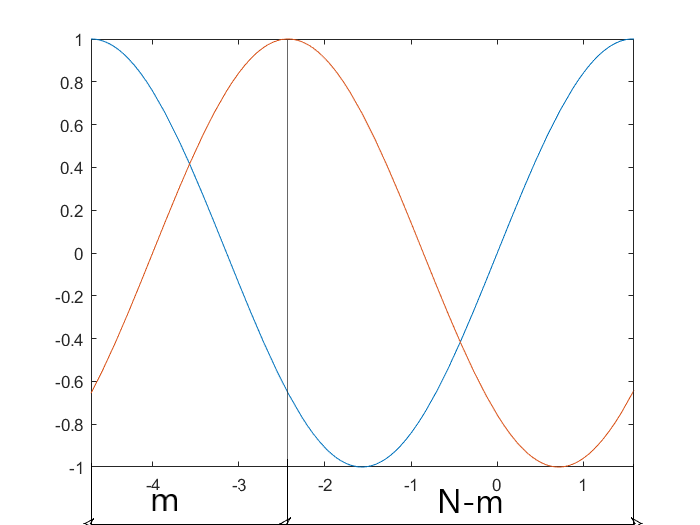
Рисунок 1 – моделирование сигналов x(n) и y(n+m) в среде Matlab
Описывая словами
процесс внутри
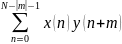можно сказать, что мы сдвигаем одну
функцию относительно другой на величину
m
и поочередно перемножаем значения x(n)
и в y(n+m)
в области их пересечения. В прикладных
задачах говорят, что площадь области
пересечения и есть числовое выражение
функции
.
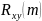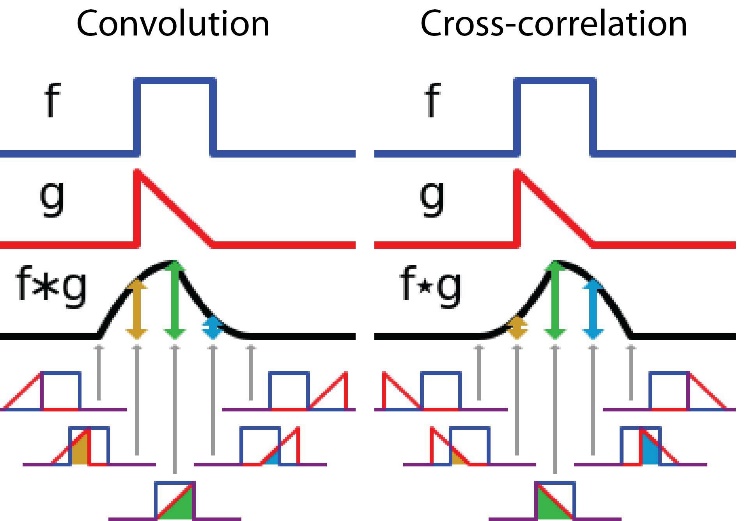
Рисунок 2 – Взаимнокорреляционная функция ВКФ
Значение КВК, рассчитанное по этим формулам, лежит в пределе от -1 до +1. Если модуль КВК приближается к единице, то это свидетельствует о существовании какого-то вида линейной связи между сигналами.
КВК, в частности, используется при анализе электроэнцефалограмм (ЭЭГ). Он позволяет оценить степень взаимосвязи между сигналами ЭЭГ, снятыми в разных зонах на поверхности головы. Результат КВК между всеми возможными парами каналов можно представить в форме корреляционной матрицы.
Нормированная оценка – значение лежит в пределах от -1 до 1.
Несмещенная оценка:
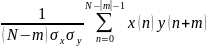
Смещенная и несмещенная оценка близки на малых сдвигах. Чаще на практике используется смещенная оценка, потому что ее вычисление проще (суть в том, что делим на разное, в этом основная разница).
Обработка результатов эксперимента
clc
close all
clear all
Fs=350;
tmax=0.8;
F=42;
T=1/Fs;
t=0:T:tmax-T;
M=5;
A(1:M)=[1 1 1 1 1];
C(1:M)=[0 0 0 0 0];
for i=1:M
Signal(:,i)=A(i)*sin(2*pi*F*t(:)-(i-1)*pi/4)+C(i);
end
figure
subplot(2,1,1)
dy=3;
for i=1:M
plot(t,Signal(:,i)-i*dy)
hold on
end
title('Графики тестовых сигналов')
subplot(2,1,2)
R=corrcoef(Signal);
Ra=zeros(M+1,M+1);
Ra(1:M,1:M)=R;
pcolor(Ra)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов')
figure
subplot(1,2,1)
Limit=0.5;
for i=1:M
for j=1:M
if R(i,j)>Limit
R1(i,j)=1;
else
R1(i,j)=0;
end
end
end
Ra1=zeros(M+1,M+1);
Ra1(1:M,1:M)=R1;
pcolor(Ra1)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов, порог = 0.5')
subplot(1,2,2)
Limit=0.85;
for i=1:M
for j=1:M
if R(i,j)>Limit
R2(i,j)=1;
else
R2(i,j)=0;
end
end
end
Ra2=zeros(M+1,M+1);
Ra2(1:M,1:M)=R2;
pcolor(Ra2)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов, порог = 0.85')
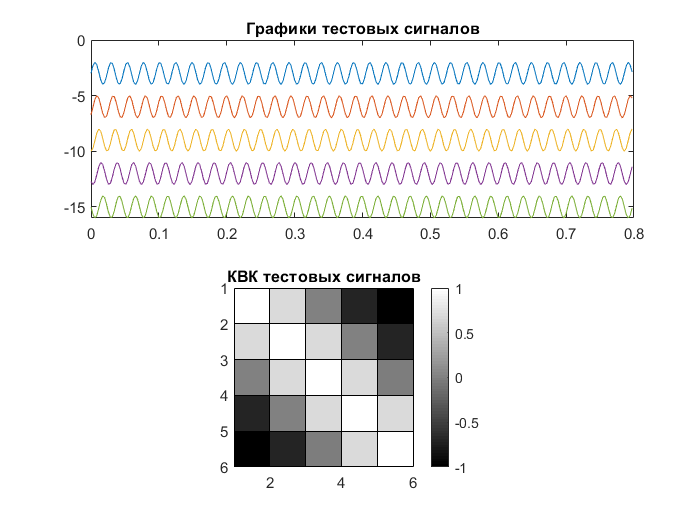
Рисунок 3 – Графики тестовых сигналов и графическое отображение корреляционной матрицы
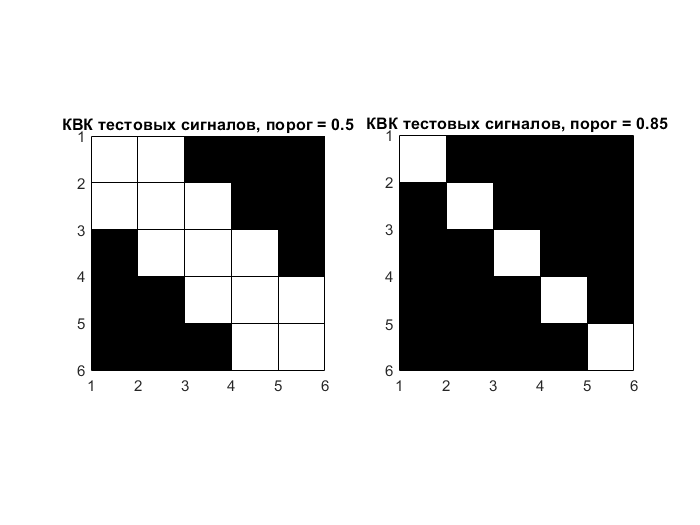
Рисунок 4 – Графическое отображение корреляционных матриц с установленным порогом 0,5 и 0,85 соответственно
clc
close all
clear all
Fs=350;
tmax=0.8;
F=42;
T=1/Fs;
t=0:T:tmax-T;
M=5;
A(1:M)=[4 3 6 1 4];
C(1:M)=[-4 0 1 -30 0.9];
for i=1:M
Signal(:,i)=A(i)*sin(2*pi*F*t(:)-(i-1)*pi/4)+C(i);
end
figure
subplot(2,1,1)
dy=10;
for i=1:M
plot(t,Signal(:,i)-i*dy)
hold on
end
title('Графики тестовых сигналов')
subplot(2,1,2)
R=corrcoef(Signal);
Ra=zeros(M+1,M+1);
Ra(1:M,1:M)=R;
pcolor(Ra)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов')
figure
subplot(1,2,1)
Limit=0.5;
for i=1:M
for j=1:M
if R(i,j)>Limit
R1(i,j)=1;
else
R1(i,j)=0;
end
end
end
Ra1=zeros(M+1,M+1);
Ra1(1:M,1:M)=R1;
pcolor(Ra1)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов, порог = 0.5')
subplot(1,2,2)
Limit=0.85;
for i=1:M
for j=1:M
if R(i,j)>Limit
R2(i,j)=1;
else
R2(i,j)=0;
end
end
end
Ra2=zeros(M+1,M+1);
Ra2(1:M,1:M)=R2;
pcolor(Ra2)
colormap(gray)
axis ij
axis square
title('КВК тестовых сигналов, порог = 0.85')
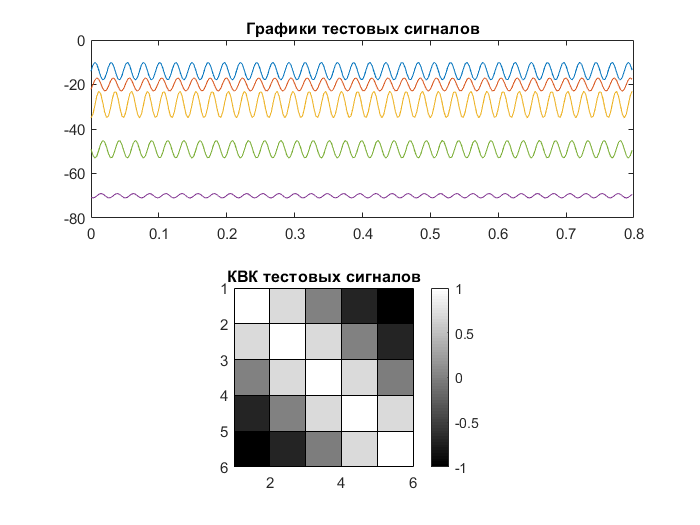
Рисунок 5 – Графики тестовых сигналов с измененной амплитудой, постоянной составляющей и графическое отображение корреляционной матрицы
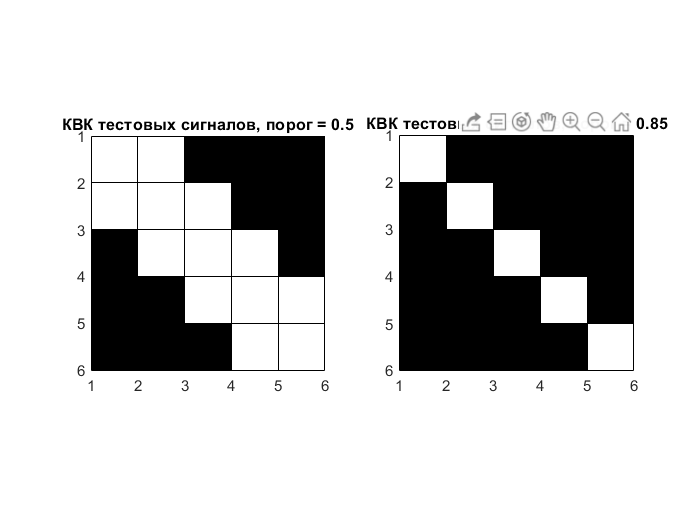
Рисунок 6 – Графическое отображение корреляционных матриц с установленным порогом 0,5 и 0,85 соответственно
clc
clear all
close all
EEG=load('R7_04.txt');
N=length(EEG(:,1));
M=length(EEG(1,:));
Fs=185;
T=1/Fs;
tmax=N*T;
t=0:T:tmax-T;
figure
subplot(2,1,1)
dy=100;
for i=1:M
plot(t,EEG(:,i)-i*dy)
hold on
end
title('Графики 16-канальной ЭЭГ')
subplot(2,1,2)
R=corrcoef(EEG);
Ra=zeros(M+1,M+1);
Ra(1:M,1:M)=R;
pcolor(Ra)
colormap(gray)
axis ij
axis square
title('КВК ЭЭГ')
figure
subplot(1,2,1)
Limit=0.5;
for i=1:M
for j=1:M
if R(i,j)>Limit
R1(i,j)=1;
else
R1(i,j)=0;
end
end
end
Ra1=zeros(M+1,M+1);
Ra1(1:M,1:M)=R1;
pcolor(Ra1)
colormap(gray)
axis ij
axis square
title('КВК ЭЭГ, порог = 0.5')
subplot(1,2,2)
Limit=0.85;
for i=1:M
for j=1:M
if R(i,j)>Limit
R2(i,j)=1;
else
R2(i,j)=0;
end
end
end
Ra2=zeros(M+1,M+1);
Ra2(1:M,1:M)=R2;
pcolor(Ra2)
colormap(gray)
axis ij
axis square
title('КВК ЭЭГ, порог = 0.85')
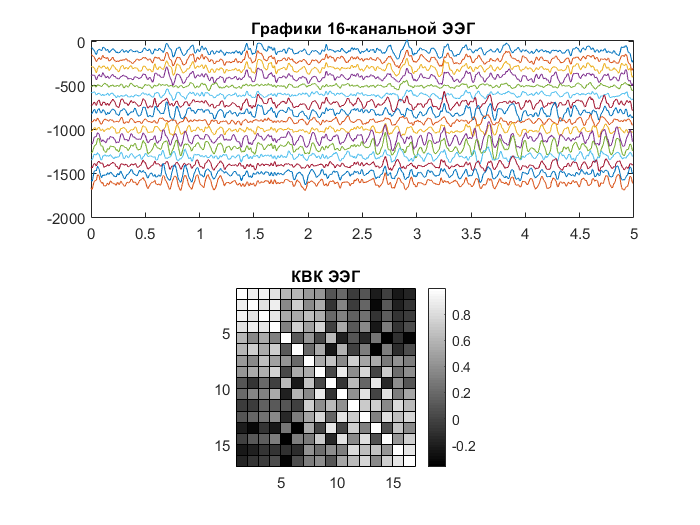
Рисунок 7 – Графики 16-канальной ЭЭГ и графическое отображение корреляционной матрицы
Рисунок 8 – Графическое отображение корреляционных матриц с установленным порогом 0,5 и 0,85 соответственно
Выводы
Т.к.
корреляционная функция предназначена
для поиска схожих закономерностей между
сигналами, то при изменении амплитуды
и постоянной составляющей (сигналы в
пункте 5 и 11) коэффициент взаимной
корреляции не поменялся. В работе
использовалась формула нормированной
смещенной оценки ВКФ, однако при небольших
значениях сдвига разница между смещенной
и несмещенной оценкой не велика. Разница
между смещенной и несмещенной оценкой
заключается в том, что при использовании
несмещенной ее математическое ожидание
равно истинной оценке ВКФ, в то время
как формула смещенной нарушает правило
усреднения, однако считается проще. По
графическому отображению матрицы ВКФ
можно заметить, что корреляционные
матрицы симметричны относительно
диагонали. Если мы имеем, например,
набор, состоящий из n тестов, то
число коэффициентов корреляции,
полученных экспериментальным путем,
составит
.
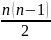Эти коэффициенты заполняют половину
матрицы, находящуюся по одну сторону
ее главной диагонали. По другую сторону
находятся, очевидно, те же коэффициенты.
Поэтому корреляционная матрица симметрична.