МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра биотехнических систем
отчет
по практическому занятию №2
по дисциплине «Моделирование биологических процессов и систем»
Тема: Анализ временных рядов
Вариант 7
Студент гр. 7501 |
|
Исаков А.О. |
Преподаватель |
|
Скоробогатова А.И. |
Санкт-Петербург
2020
Цель работы: написать программу для анализа одномерного временного ряда.
Основные теоретические положения
Анализ временных рядов (time-series analysis) – совокупность статистических методов для выявления, составляющих временного ряда и его прогнозирования.
Временной ряд – последовательность статистических данных, собранных в разные моменты времени, о значении каких-либо параметров исследуемого процесса.
Временные ряды, как правило, возникают в результате измерения некоторого показателя, а основной целью их анализа является построение прогноза значений ряда на будущие периоды. Основные задачи анализа временного ряда – понять, под воздействием каких компонент формируется значение временного ряда, и построить математическую модель для каждой компоненты или их совокупности.
В данной работе используются два метода анализа временного ряда:
Метод скользящего среднего;
Экспоненциальное сглаживание.
Метод скользящего среднего
Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина "окна". Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием, скользящим средним, состоит в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более "надежным" кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более "зубчатым" кривым, чем сглаживание скользящим средним.
Экспоненциальное сглаживание
Простая и прагматически ясная модель временного ряда имеет следующий вид:
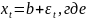
b – константа и
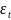– случайная ошибка. Константа b
относительно стабильна на каждом
временном интервале, но может также
медленно изменяться со временем. Один
из интуитивно ясных способов выделения
b состоит в том, чтобы использовать
сглаживание скользящим средним, в
котором последним наблюдениям
приписываются большие веса, чем
предпоследним, предпоследним большие
веса, чем пред-предпоследним и т.д.
Простое экспоненциальное именно так и
устроено: здесь более старым наблюдениям
приписываются экспоненциально убывающие
веса, при этом, в отличие от скользящего
среднего, учитываются все предшествующие
наблюдения ряда, а не те, что попали в
определенное окно. Точная формула
простого экспоненциального сглаживания
имеет следующий вид:
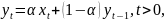
где
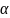– коэффициент сглаживания, который
принимает значения от 0 до 1 и определяет,
насколько быстро уменьшается вес для
предыдущих наблюдений.
Когда эта формула применяется рекурсивно,
то каждое новое сглаженное значение,
которое является также прогнозом,
вычисляется как взвешенное среднее
текущего наблюдения и сглаженного ряда.
Очевидно, результат сглаживания зависит
от параметра
.
Если
,
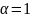то предыдущие наблюдения полностью
игнорируются. Если
,
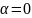то игнорируются текущие наблюдения.
Значения
между 0 и 1 дают промежуточные результаты.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
clc
clear
close all
%% Загрузка данных
num = xlsread('ts1.xlsx','Лист1','G1:G600');
%% Построить временной ряд
figure
limeline = timeseries(num(:,1), 1:600,'name', 'testing');
plot(limeline)
title('Временной ряд')
xlabel('Временные отсчеты')
ylabel('Сигнал')
%% Расчет скользящего среднего
figure
smoothedData = smoothdata(num,'movmean',600);
plot(num,'LineWidth',0.9)
hold on
plot(smoothedData,'LineWidth',1.2)
title('Реализован расчет скользящего среднего в окне w')
%% Экспоненциальное сглаживание
figure
smoothDataExp = smoothdata(num,'movmean','SmoothingFactor',1);
plot(num,'LineWidth',0.9)
hold on
plot(smoothDataExp,'LineWidth',1.2)
title('Реализовано экспоненциальное сглаживание')
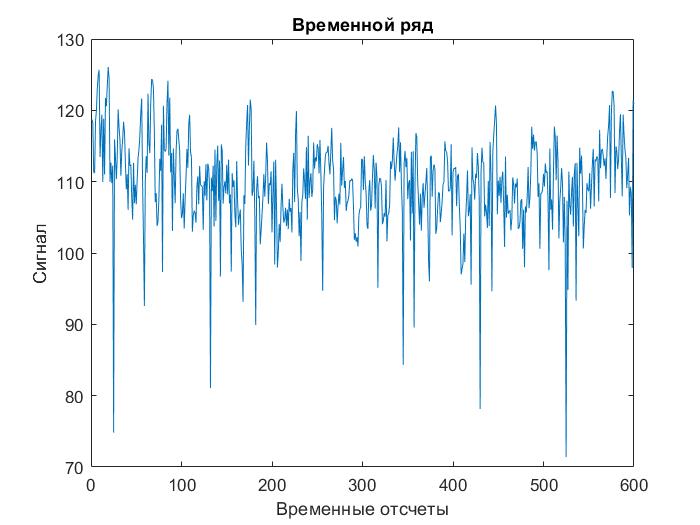
Рисунок 1 – Построение временного ряда
Метод скользящего среднего
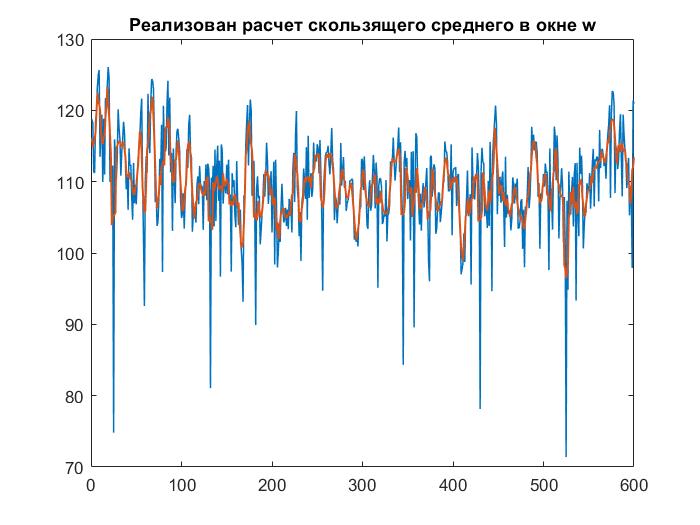
Рисунок 2 – Построение скользящего среднего с шириной окна 5
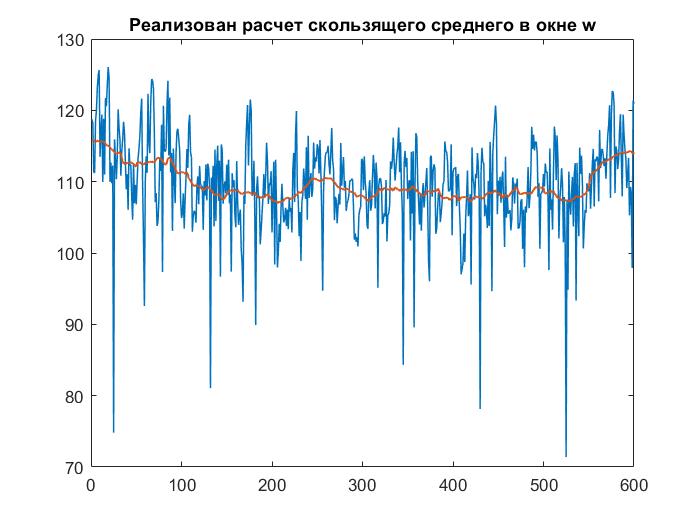
Рисунок 3 – Построение скользящего среднего с шириной окна 50
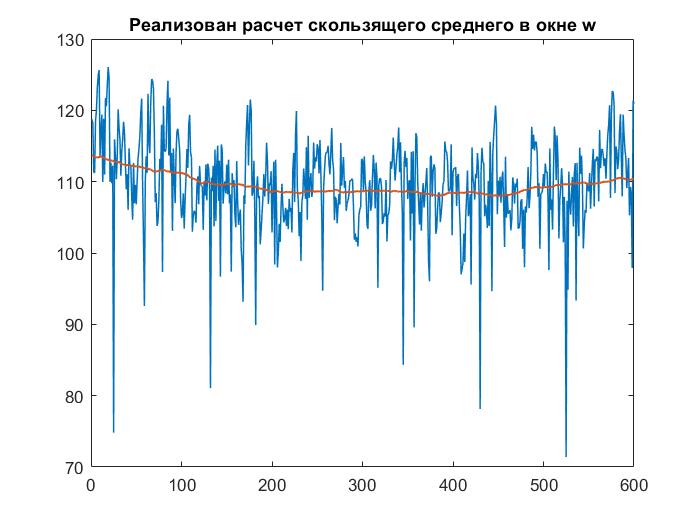
Рисунок 4 – Построение скользящего среднего с шириной окна 200
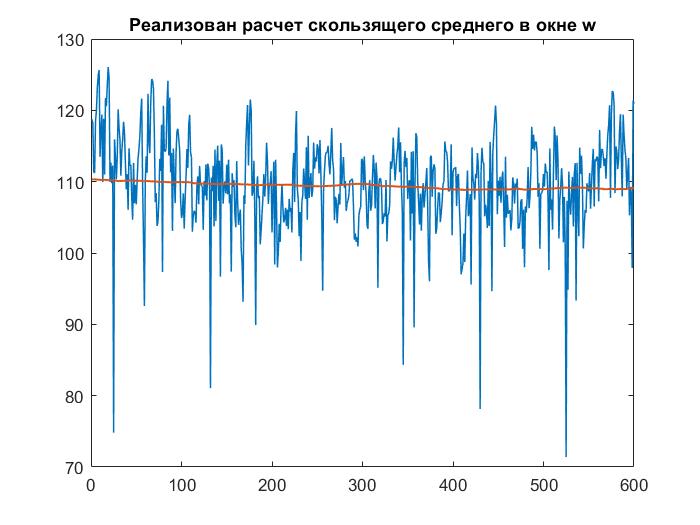
Рисунок 5 – Построение скользящего среднего с шириной окна 600
Экспоненциальное сглаживание
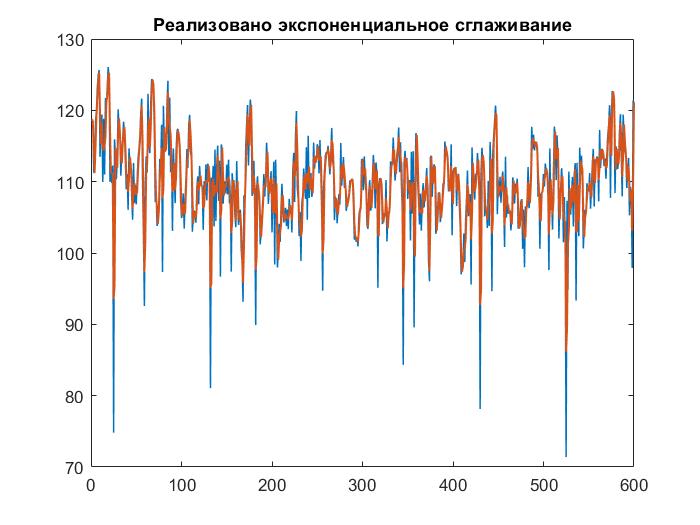
Рисунок
6 – Построение экспоненциального
сглаживания с
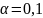
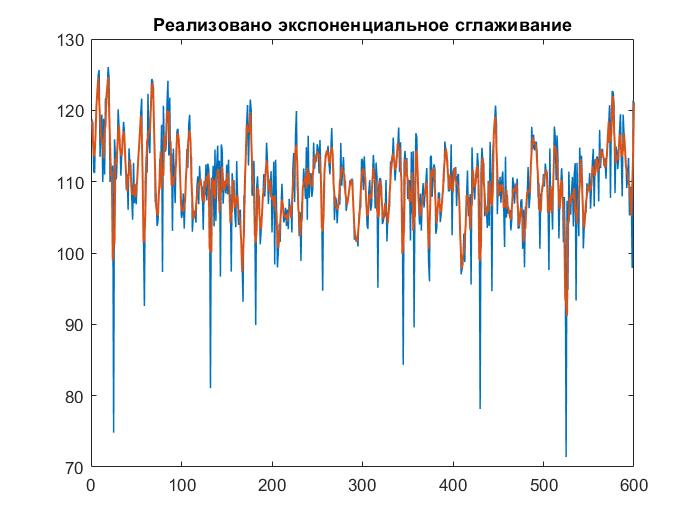
Рисунок
7 – Построение экспоненциального
сглаживания с
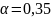
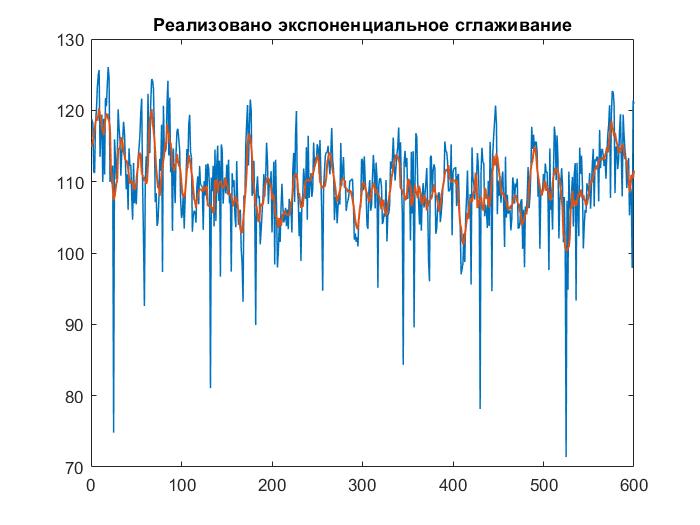
Рисунок
8 – Построение экспоненциального
сглаживания с
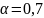
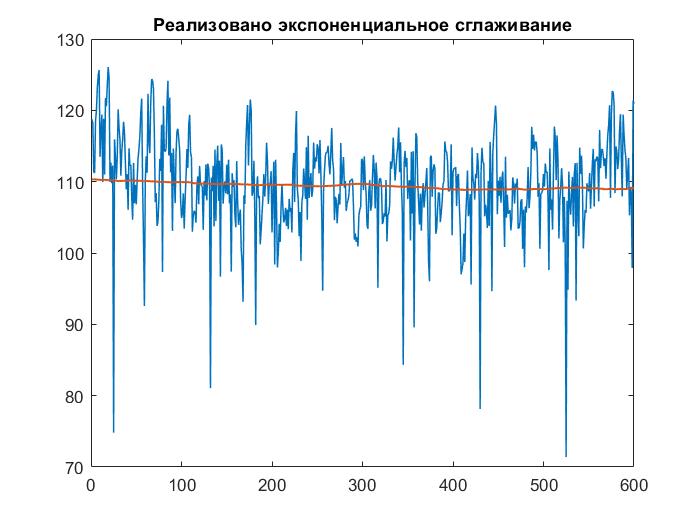
Рисунок 9 – Построение экспоненциального сглаживания с
ВЫВОД
В ходе данной работы был произведен анализ тенденции временного ряда с помощью двух методов: скользящего среднего (наблюдали зависимость выходного сигнала относительно изменения параметра ширины «окна сглаживания» у входного) и экспоненциального сглаживания (аналогично изменяли коэффициент сглаживания от 0,1 до 1). Между собой методы отличаются алгоритмами, хотя дают схожие результаты (см. рис. 2 – 9), при тщательном правильном подборе коэффициентов.