

Лекция №4 по ЦОС
Примеры спектров и корреляционных функций некоторых сигналов и СПМ (спектральная плотность мощности)
Пример 1. Центрированный прямоугольный импульс |
|
|||||
|
1, |
2 |
|
2 |
→ | | |
1.29 |
0, |
|
| | 22 |
||||
|
2 |
2 |
|
|
Если взять и подставить интеграл, получим спектр: |
1.30 |
|||
∙ |
sin % |
∙ &'( % |
||
|
|
% |
|
1.31 |
|
sinc x ,-./ / |
|
||
Спектральная плотность мощности: |
|
|
|
sin % |
|
|
|
0 | | |
|
|
∙ |
1.32 |
|||
|
|
% |
|
||||
1

Корреляционная функция: |
|
|
|||
|
2 |
, |
1 2 3 2 |
|
|
0 2 |
а равна площади пересечения |
1.33 |
|||
2 3 |
, |
2 4 0 |
|||
0, |
|
|
|2| |
|
|
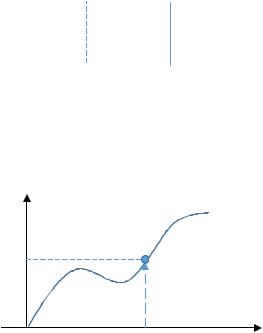
получается в результате перемножения сдвинутых версий сигнала и последующего2 интегрирования. Численно результат такого перемножения в момент времени равен площади пересечения сдвинутых сигналов (см.ниже рисунок)
22
1 2 так же можно было найти, взяв обратное преобразование Фурье от 0 (1.32) (т.е. по теореме Винера-Хинчина).
Пример 2. Нецентрированный прямоугольный импульс
F
Спектр сигнала и спектральная |
плотность |
соответственно |
, |
равны |
: |
|
|
|
||||||||
H |
2, |
|
|
|
|
|
|
% |
|
|
1.34 |
|||||
C DEFG DE G ∙ |
∙ H ∙ &'( |
∙ H |
||||||||||||||
|
|
|
|
|
|
∙ sin |
|
% |
|
|
|
|
∙ &'( |
|
% |
1.35 |
0 C ∙ C ∙ 0 |
|
|
% |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Т. е., спектральные плотности у центрированного и нецентрированного сигнала сов- |
||||||||||||||||||||
падают. Отсюда |
же |
следует, |
что амплитудный |
спектр нецентрированного сигнала |
||||||||||||||||||
ногоM |
сигналаC |
|
|
|
|
|
|
|
тоже совпадает с амплитудным спектром центрирован- |
|||||||||||||
Единственное что будет изменяться |
– |
это фаза и |
, |
соответственно |
, |
ФЧХ |
|
|||||||||||||||
P |
N |
. N ∙ &'( |
%, |
|
|
|
|
|
|
. |
|
|||||||||||
|
|
Корреляционная функция: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 C 2 DO P0 C Q DOE0 G 1 2 |
|
1.36 |
|||||||||||||
|
|
Основные соотношения связаны парой (прямого и обратного) преобразований Фурье |
||||||||||||||||||||
D ∙ , DO ∙ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Выпишем три основных соотношения для теории непрерывных сигналов, связанные |
||||||||||||||||||||
с парой преобразований Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) |
|
→ , |
используя D ∙ |
|
|
|
|
|
|
|
|
|
|
|||||||||
→ |
, |
используя DO ∙ |
|
|
|
|
|
|
|
|
|
(1.37) |
||||||||||
2) |
1 2 → 0 , |
используя D ∙ |
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
→ 1 2 , используя DO ∙ |
|
|
|
|
|
|
|
|
(1.38) |
||||||||||||
3) |
V → W , |
используя D ∙ |
|
|
|
|
|
|
|
|
|
|
||||||||||
W → V , |
используя DO ∙ |
|
|
|
|
|
|
|
|
|
(1.39) |
|||||||||||
|
|
Определение (скалярного) произведения двух непрерывных сигналов: |
|
|
|
|||||||||||||||||
|
|
Пусть |
|
|
и |
|
е., |
– |
два непрерывных, в общем случае, комплексных сигнала с ко- |
|||||||||||||
нечной |
энергий |
т |
|
энергией |
|
, |
тогда их скалярным произведением |
|||||||||||||||
|
|
|
|
, |
|
.X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
называется величина: |
|
|
|
|
Y 4 ∞, Y[ 4 ∞ |
|
|
|
|
|
|
1.40 |
||||||||||
|
|
|
|
|
|
4 , X X ] ^_ 3 `a; _, a cd |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В частном случае, когда X: |
|
|
|
|
|
|
|
1.41 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 , Y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пусть сигнал |
любой непрерывный комплексный сигнал с конечной энергией |
|||||||||||||||||||
|
|
, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Y 4 ∞ |
|
|
|
|
|
|
|
|
N| |N eY e4 , |
|
|
|
|
|
1.42 |
|||||||
|
|
По смыслу, N| |Nсовпадает со среднеквадратическим значением сигнала. |
|
|
|
|||||||||||||||||
|
|
Пусть сигналы |
|
и |
X |
имеют конечную энергию |
, |
тогда расстоянием между эти |
- |
|||||||||||||
ми сигналами |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|||||||||
называется величина
3

|
|
|
N| |N |
1.43 |
|
f , X N| X|N g | |
X | |
||||
|
|
|
|
|
|
Из формулы (1.43) следует, что расстояние между двумя сигналами определяется как |
|||||
норма разностного сигнала |
X. |
|
|
|
|
Обобщенное равенство Парсеваля: |
X ∙ h |
1.44 |
|||
4 , X 4 , h 4 |
|||||
|
|
|
|
|
|
В частном случае, когда X, получаем классическое равенство Парсеваля: |
1.45 |
||||
Y || |
0 |
|
|||
|
|
|
|
|
|
2. Основные понятия из теории дискретных сигналов
2.1. Дискретизация непрерывных сигналов. Понятия дискретного спектра, дис-
|
кретной корреляционной функции, дискретной СПМ. |
|
||||
Пусть задан непрерывный, в общем случае, комплексный сигнал |
|
с конечной |
||||
энергией |
, тогда модель (процедура) дискретизации |
описывается следующим вы |
||||
|
|
- |
||||
ражениемY: 4 ∞ |
l |
& ∙ ∆ , & 0, n1, n2 |
2.1 |
|||
|
i j&k |
|||||
|
|
0 → l 1 |
|
|
||
|
l o3∞, |
|
|
|||
где l – |
0, |
0 |
|
|
|
|
дельта-функция Дирака. |
|
|
|
|
|
|
Обоснование модели дискретизации (2.1) основывается на фильтрующем свойстве
-функции: |
2.2 |
Cpq l F F, F R ∞, ∞ |
|
Cq |
|
4
F
Очевидно, из свойства (2.2) непосредственно следует справедливость модели дискретизации (2.1)
F
F
F
5
