Ордена Трудового Красного знамени
Федеральное Государственное
бюджетное образовательное учреждение
высшего образования
_______________________________________________
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
СВЯЗИ И ИНФОРМАТИКИ
Кафедра общей теории связи
ЛАБОРАТОРНАЯ РАБОТА
№ 26-3
по дисциплине «Цифровая обработка сигналов»
на тему:
«Анализ цифровых фильтров 1-го и 2-го порядков и их эмпирический синтез»
Вариант: (по бригаде) №1вариант
и (по списку - 19 вариант)
Выполнил: студент группы *******
*****************
Проверил: Терехов А.Н.
___________________
Москва 2020
1. Цель работы
На персональном компьютере провести анализ нерекурсивных и рекурсивных цифровых фильтров (ЦФ) 1-го и 2-го порядка; провести эмпирический синтез ЦФ для типовых прототипов (ФНЧ, ФВЧ и др.) в рамках полного ЦФ второго порядка.
2. Домашнее задание
2.1. Исходные данные для расчета
Исходные данные в соответствии с номером бригады сведены в таблицу 1.
Таблица 1. Исходные данные для расчетов.
№ варианта |
Коэффициенты числителя системной функции ЦФ |
Коэффициенты знаменателя системной функции ЦФ |
||||
b0 |
b1 |
b2 |
a1 |
a2 |
||
1 |
0,4 |
0,5 |
0,1 |
0,2 |
0,7 |
|
2.2. Выполнение домашнего задания
Для данных из таблицы 1 записать разностное уравнение:
Разностное уравнение ЦФ записывается в виде
(1)
где {
}
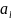и {
}
– совокупности коэффициентов ЦФ, {
}
и {
}-
задержанные (соответственно на m
и l
периодов дискретизации) копии входного
и выходного сигналов ЦФ.
В соответствии с номером бригады и формулой (1) разностное уравнение заданного ЦФ будет иметь вид:
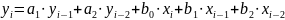(2)
Подставив в формулу (2) коэффициенты из таблицы 1, получим:
(3)
Изобразить структурную каноническую схему ЦФ:
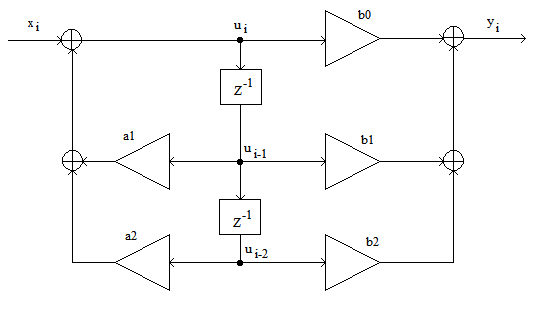
Рисунок 1 – Структурная каноническая схема ЦФ
Рассчитать значения импульсной реакции ЦФ и построить её временную диаграмму:
Импульсной реакцией называется отклик ЦФ на входной единичный импульс:
(4)
График импульсной
характеристики
,
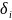построенный в соответствии с заданными
параметрами и определением импульсной
реакции, показан на рисунке 3.
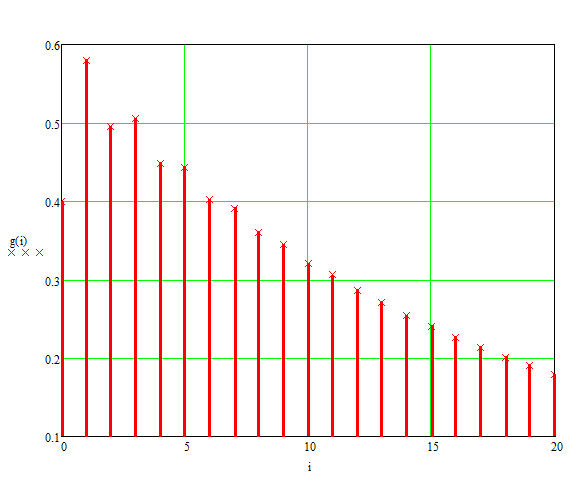
Рисунок 3 – Импульсная реакция ЦФ
Записать выражение для системной функции ЦФ и получить аналитическое выражение для его амплитудно-частотной характеристики (АЧХ):
Системная функция ЦФ определяется отношением z-преобразования отклика Y(z) и z-преобразования входного воздействия X(z). Применяя к правой и левой частям разностного уравнения (1) ЦФ прямое z-преобразование и используя свойства последнего, получаем следующий вид его системной функции:
(5)
В соответствии с номером бригады и формулой (5) системная функция будет иметь вид:
(6)
Передаточная и
системная функции ЦФ связаны равенством:
.
При определении АЧХ и ФЧХ его передаточную
функцию нужно представить в следующем
виде:
.
Где
является модулем функции
и соответственно АЧХ. Тогда, при
подстановке
в найденную нами системную функцию, мы
получим уравнение вида:
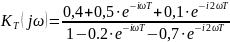(7)
Отсюда мы можем найти АЧХ ЦФ, которая ищется по формуле:
(8)
Тогда:
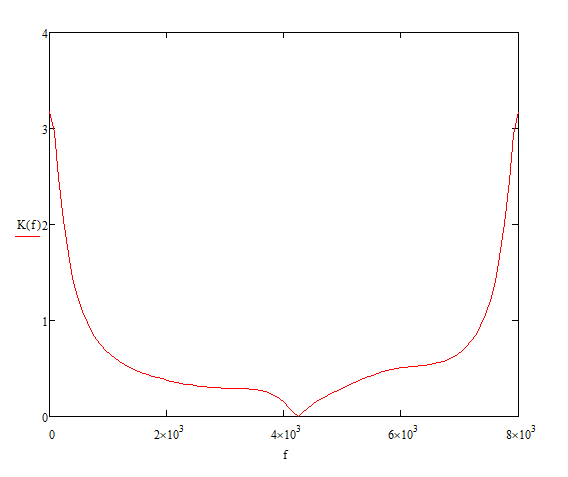
Рисунок 4 – АЧХ заданного рекурсивного ЦФ 2-го порядка
Рассчитать нули и полюса системной функции ЦФ. Определить, является ли данный фильтр устойчивым.
Нули системной функции:
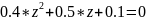
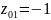
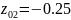
Полюса системной функции:
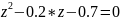
ЦФ устойчив, так как
Ход выполнения лабораторной работы:
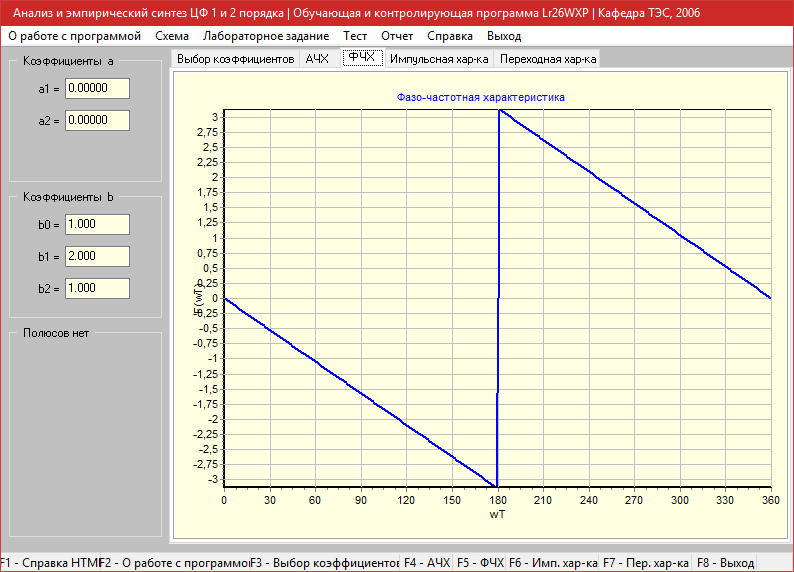
Этап 1 (a1=0, a2=0).
b1=2, b2=1
Амплитудно-частотная характеристика
Фазо-частотная характеристика
Импульсная характеристика
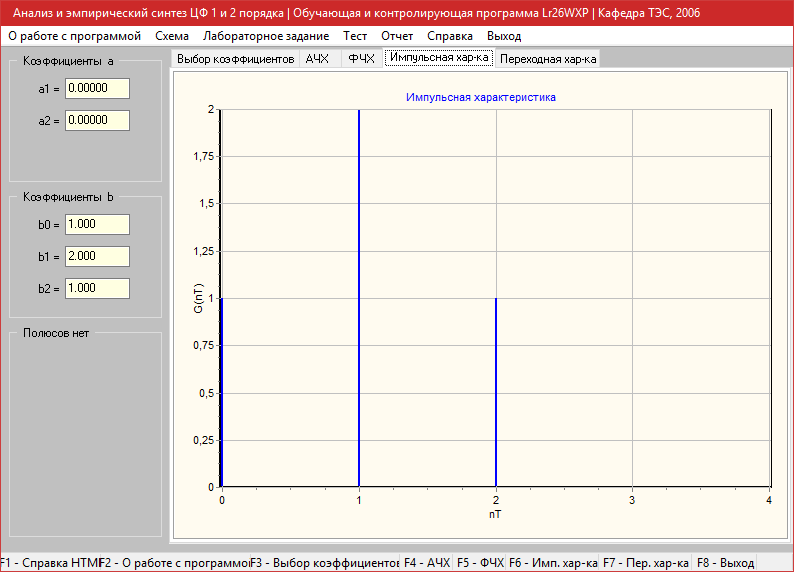
Переходная характеристика
b1=-2, b2=1
Амплитудно-частотная характеристика
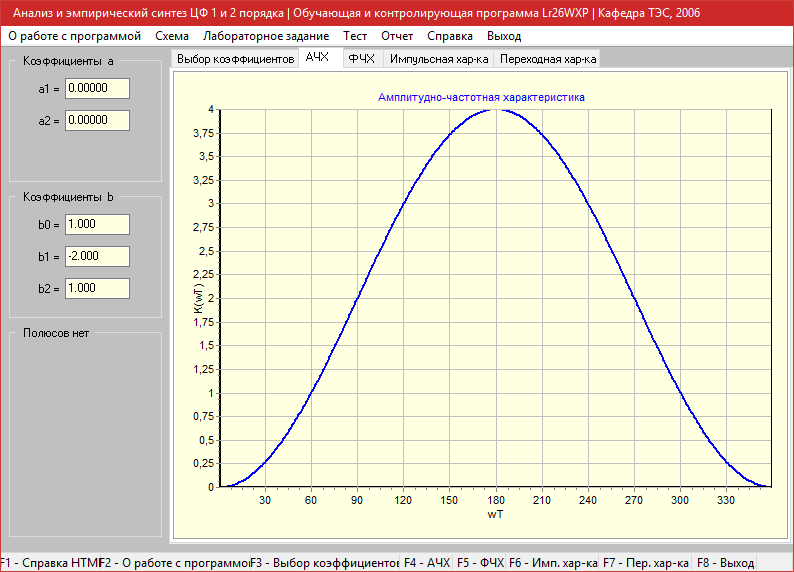
Фазо-частотная характеристика
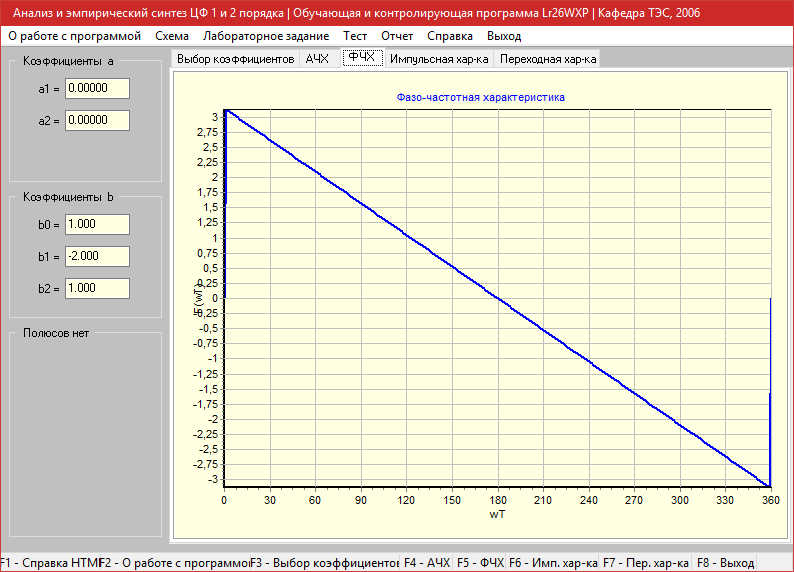
Импульсная характеристика
Переходная характеристика
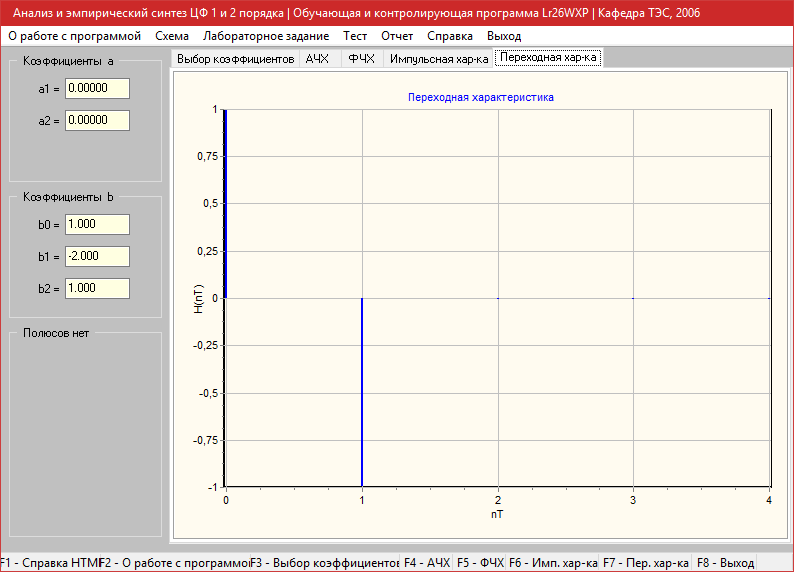
Этап 2 (b0=1, b1=0, b2=0).
a1=0.35, a2=-0.2
Амплитудно-частотная характеристика
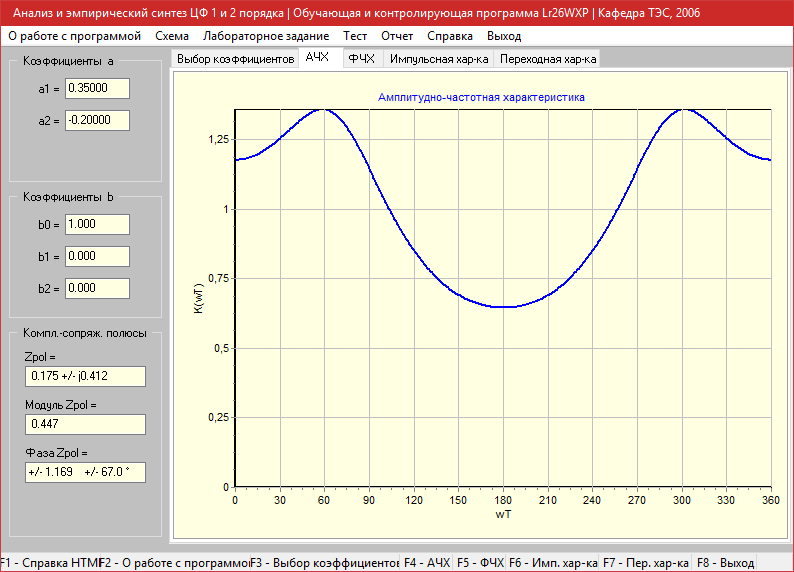
Фазо-частотная характеристика
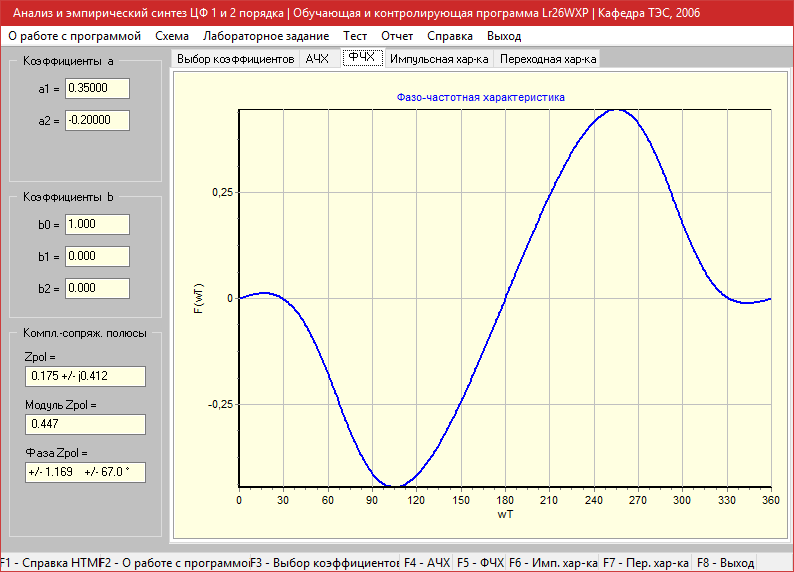
Импульсная характеристика
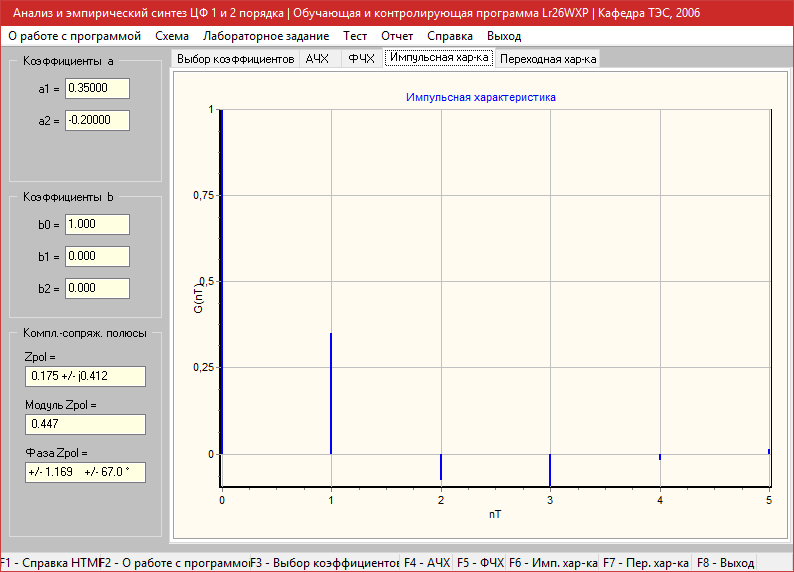
Переходная характеристика
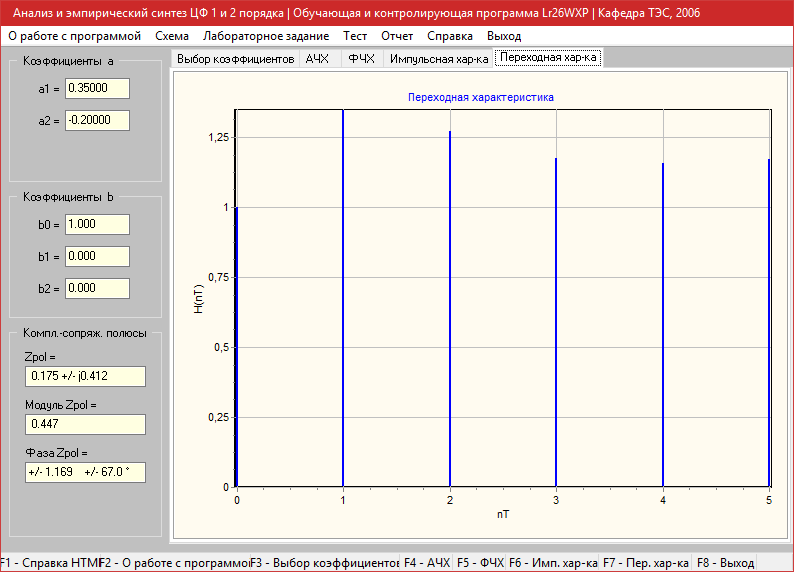
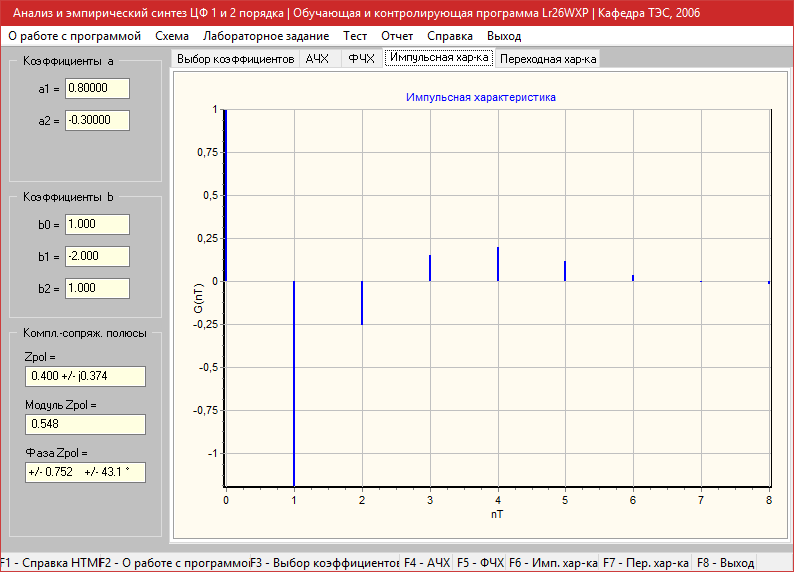
a1=0.8, a2=-0.3
Амплитудно-частотная характеристика
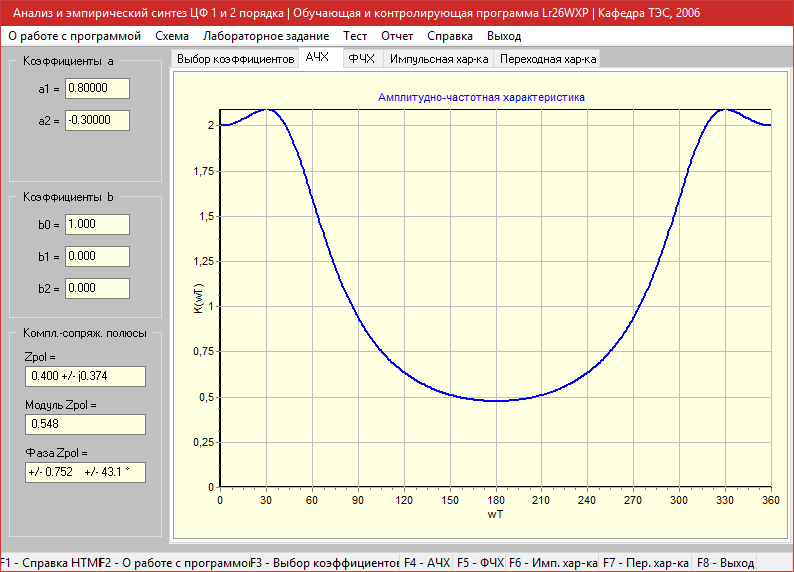
Фазо-частотная характеристика
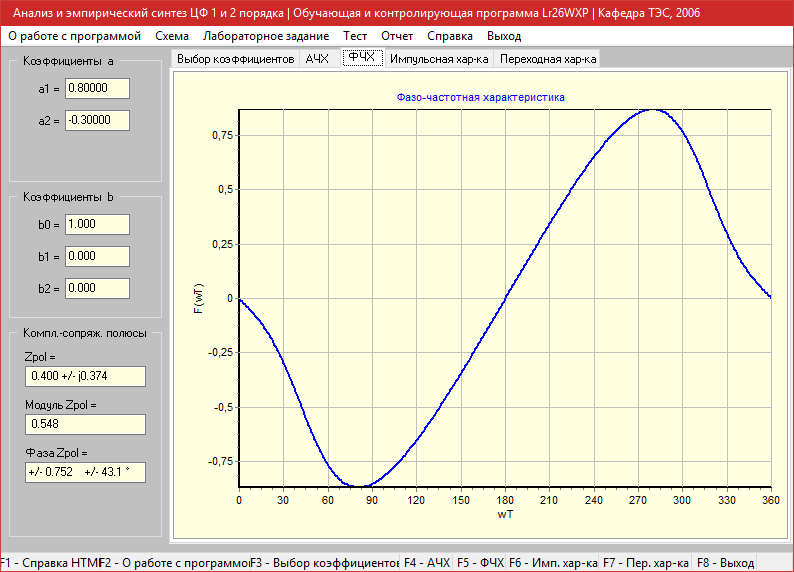
Импульсная характеристика
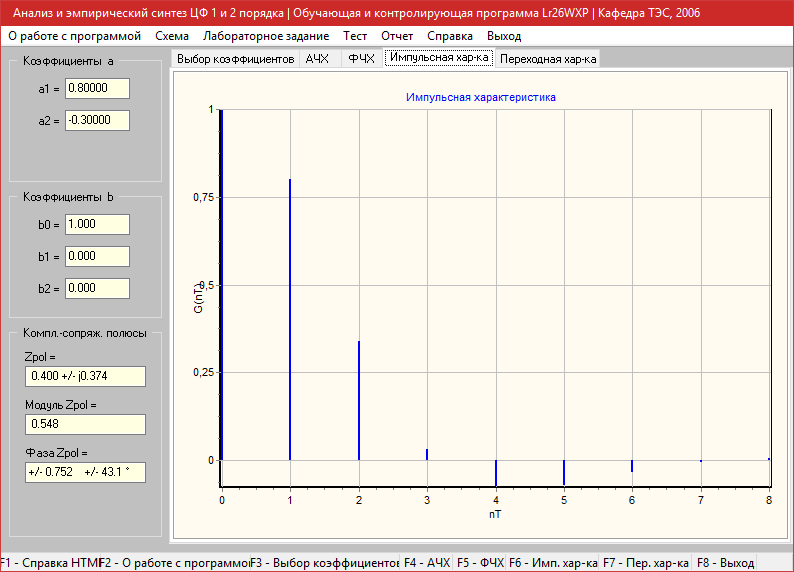
Переходная характеристика
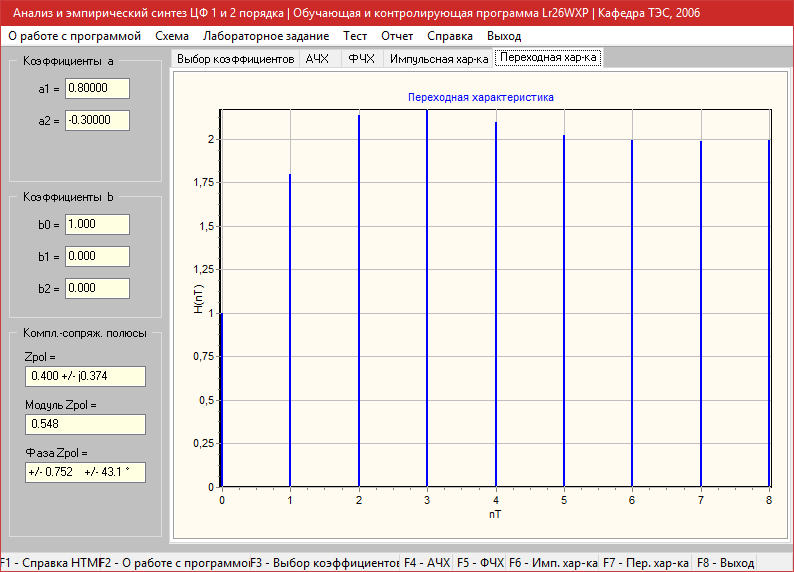
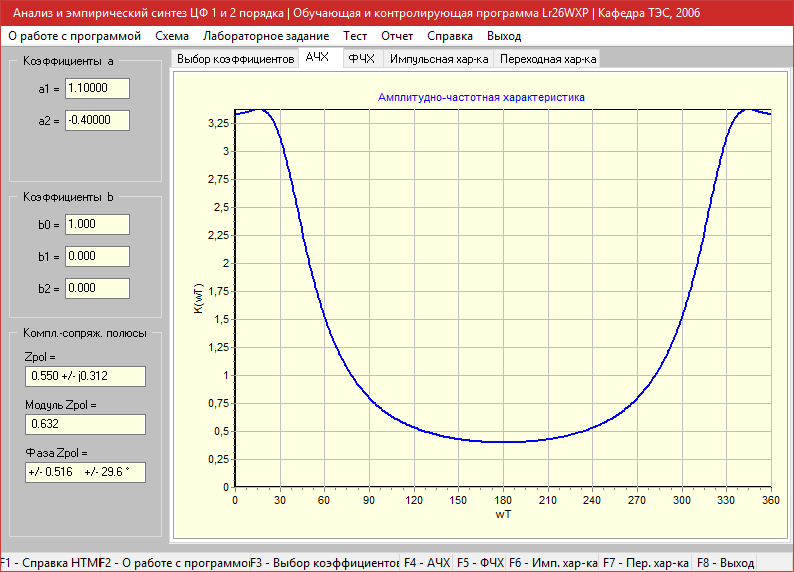
a1=1.1, a2=-0.4
Амплитудно-частотная характеристика
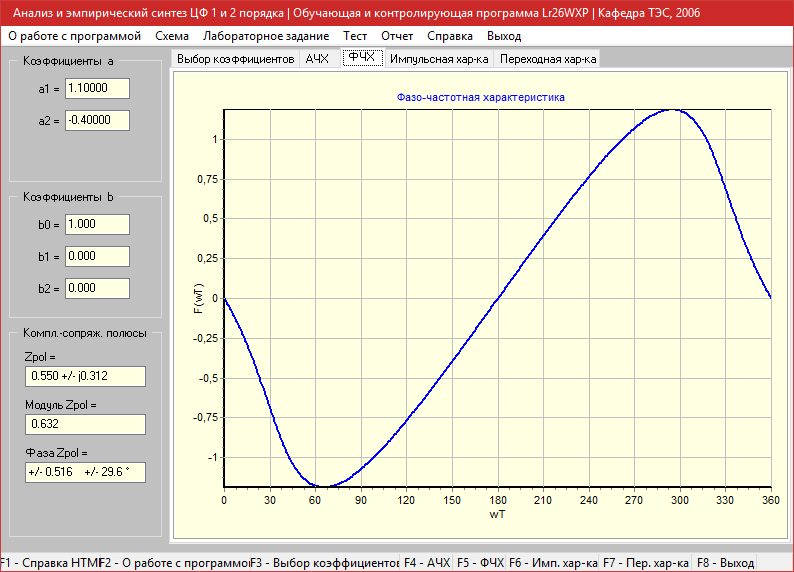
Фазо-частотная характеристика
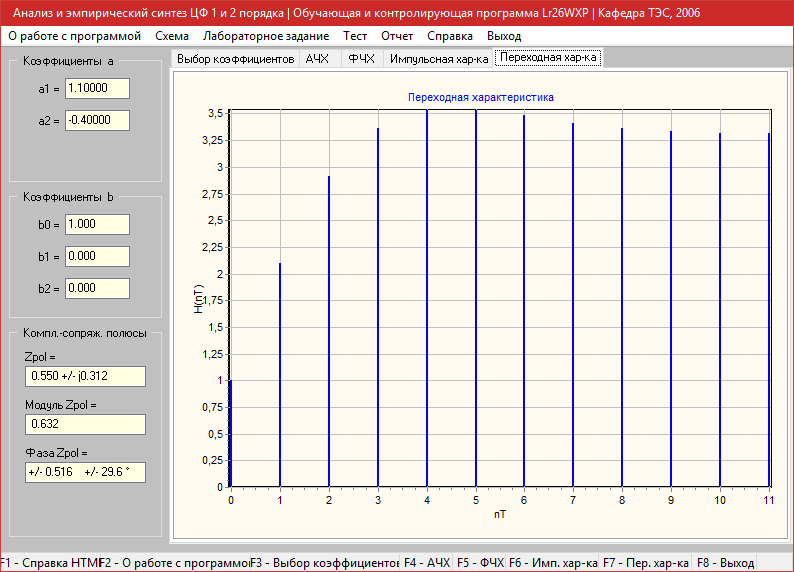
Импульсная характеристика
Переходная характеристика
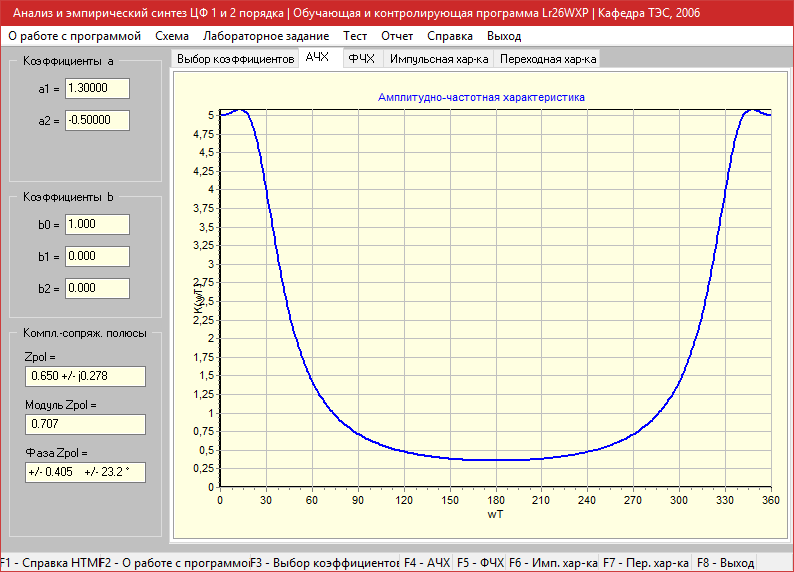
a1=1.3, a2=-0.5
Амплитудно-частотная характеристика
Фазо-частотная характеристика
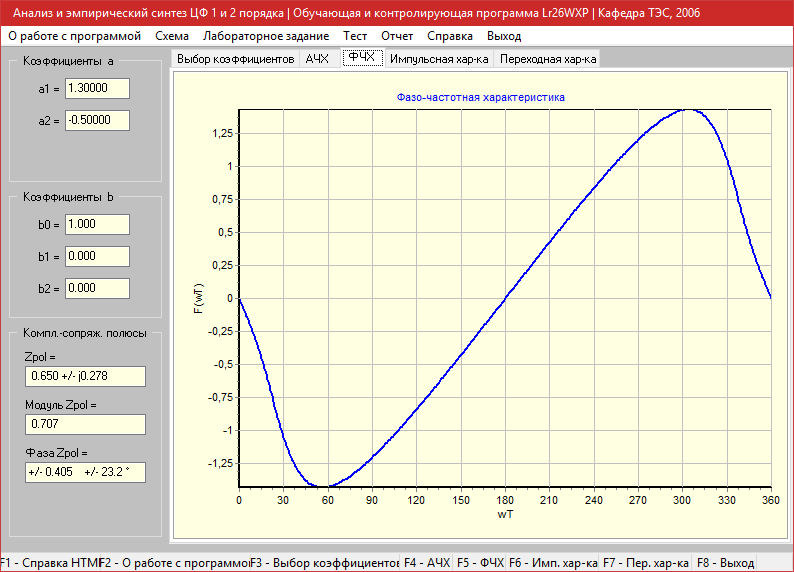
Импульсная характеристика
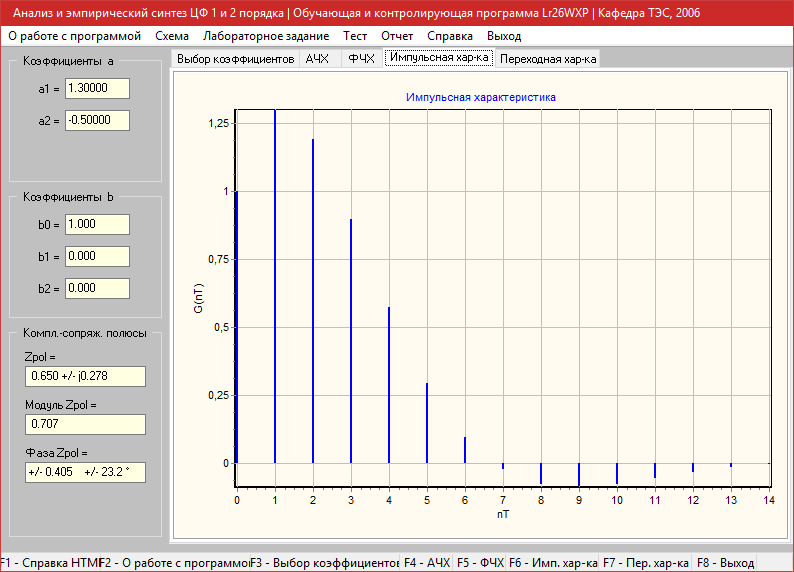
Переходная характеристика
Этап 3.
b1=2, b2=1
a1=0.35, a2=-0.2
Амплитудно-частотная характеристика
Фазо-частотная характеристика
Импульсная характеристика
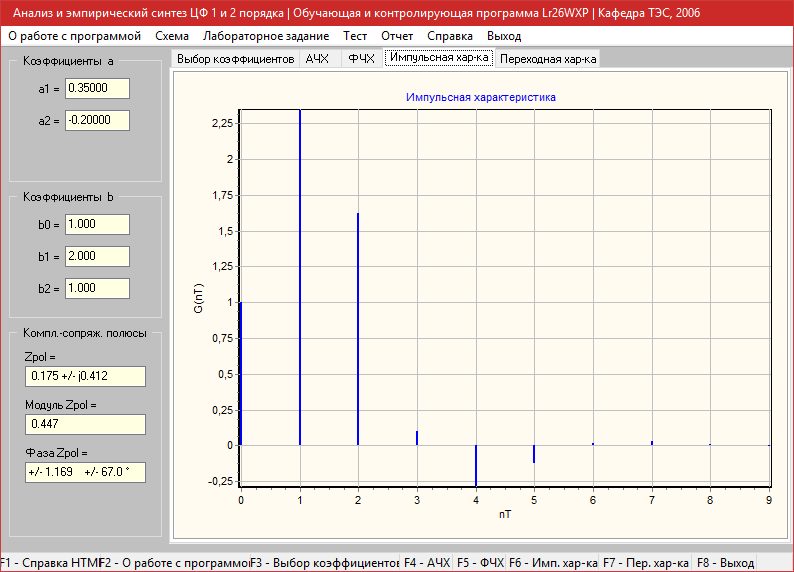
Переходная характеристика
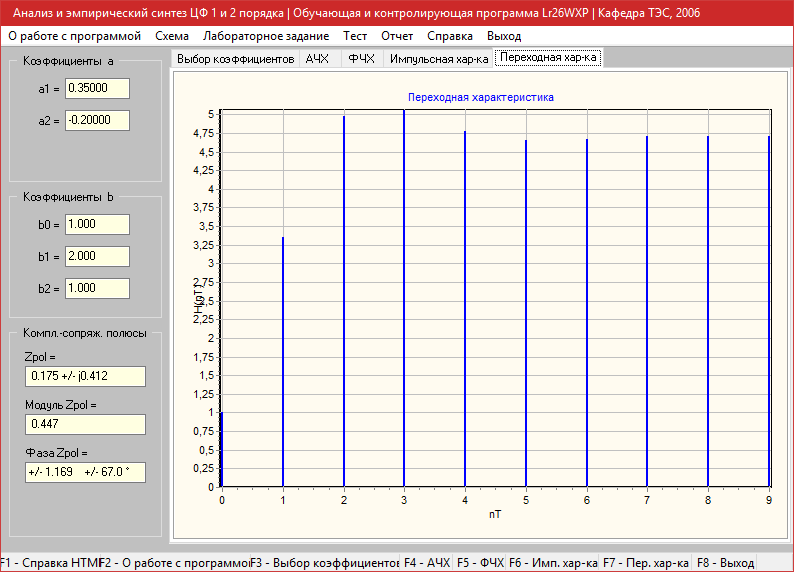
a1=0.8, a2=-0.3
Амплитудно-частотная характеристика
Фазо-частотная характеристика
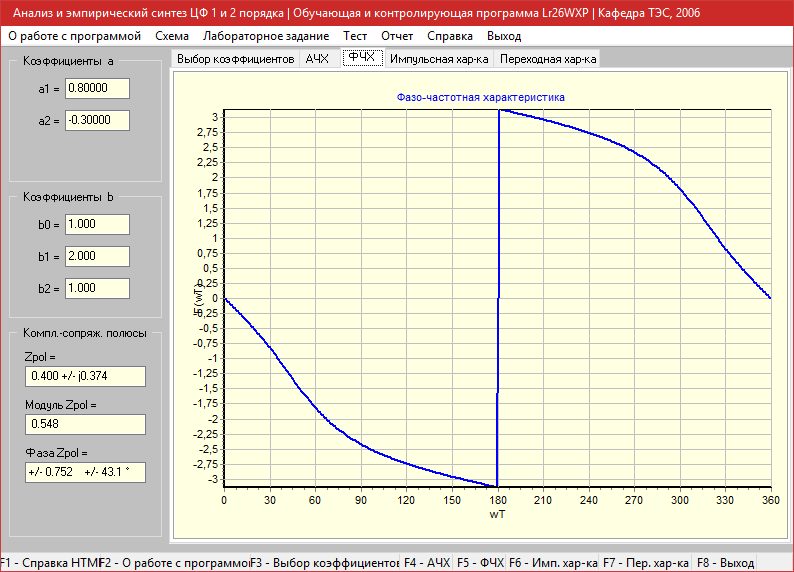
Импульсная характеристика
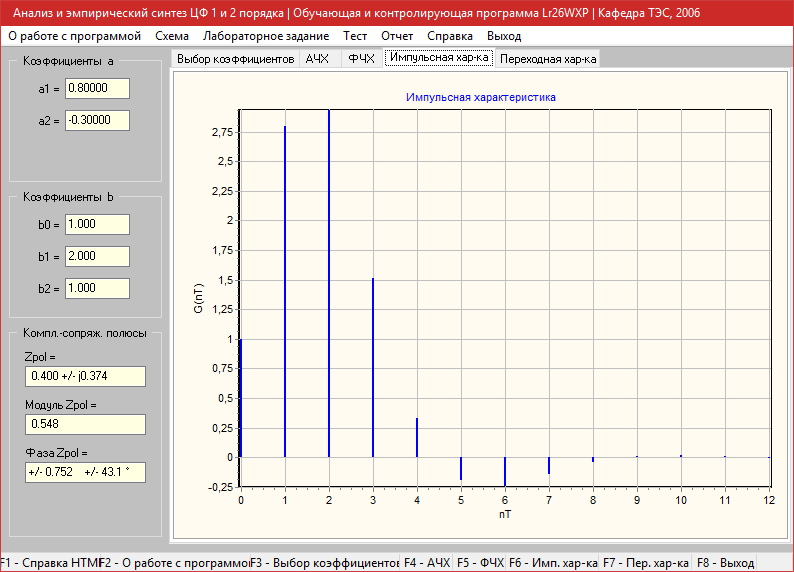
Переходная характеристика
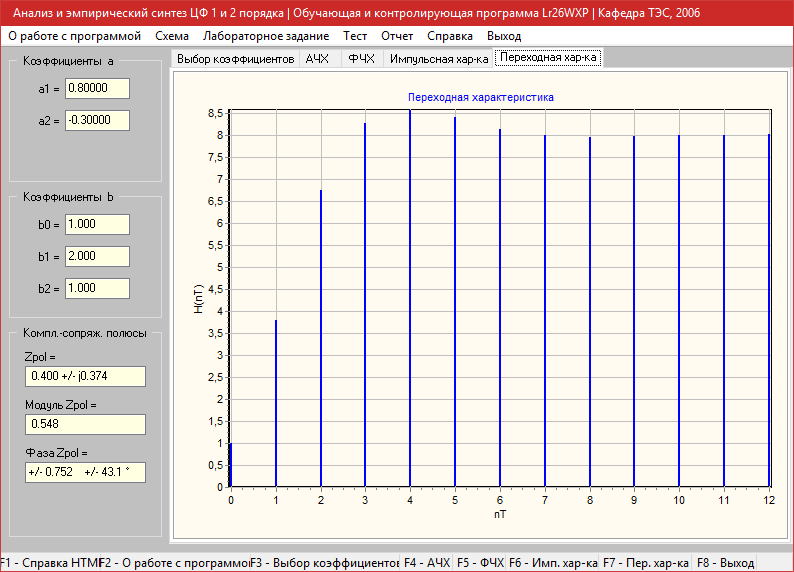
a1=1.1, a2=-0.4
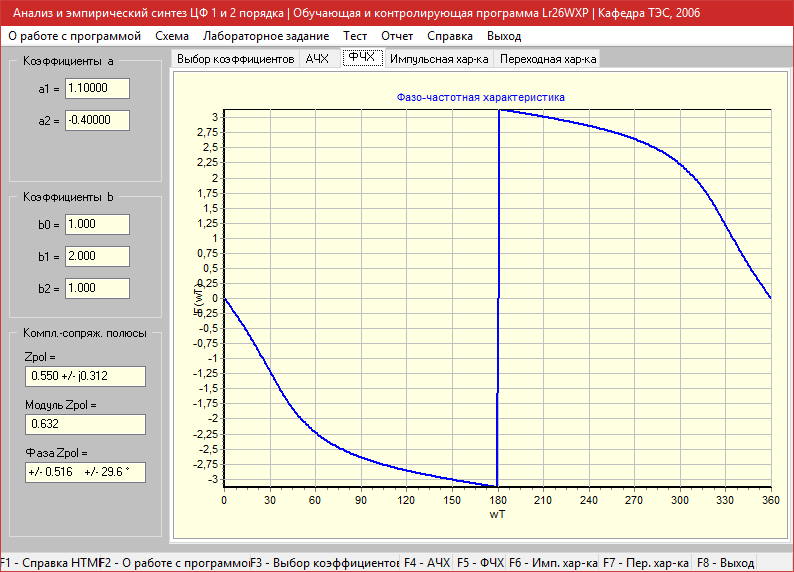
Амплитудно-частотная характеристика
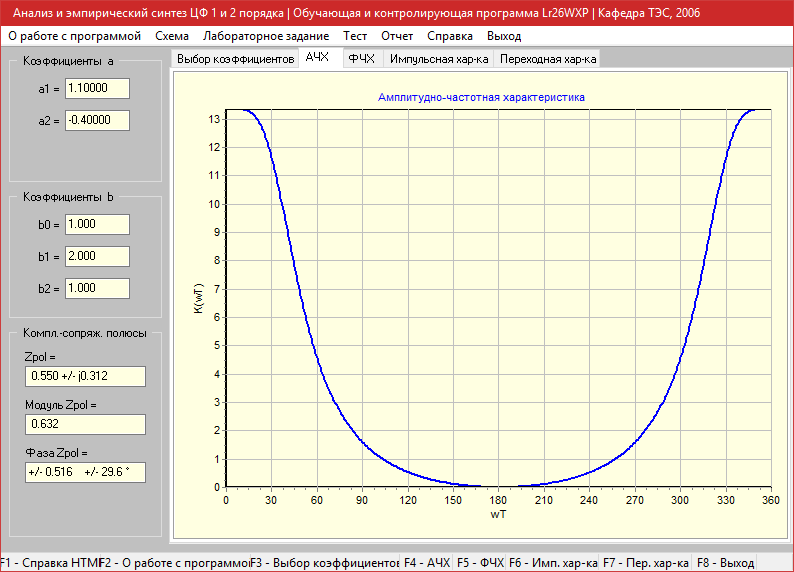
Фазо-частотная характеристика
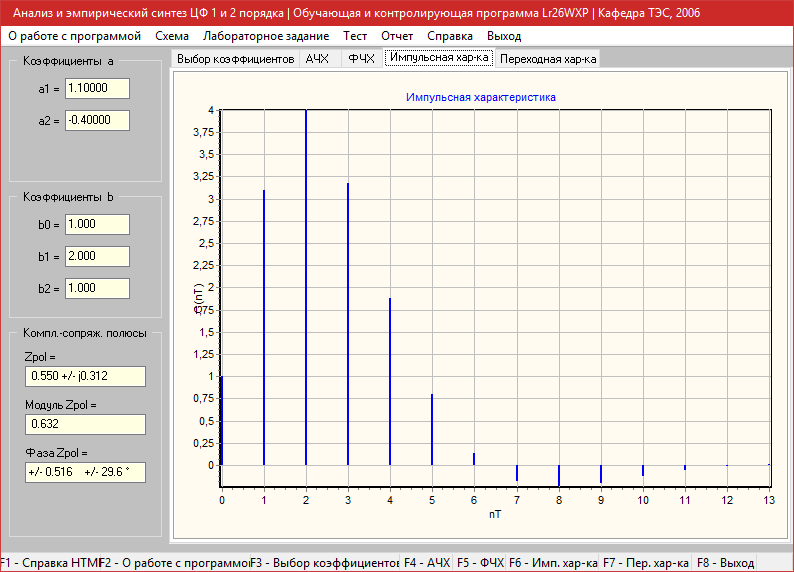
Импульсная характеристика
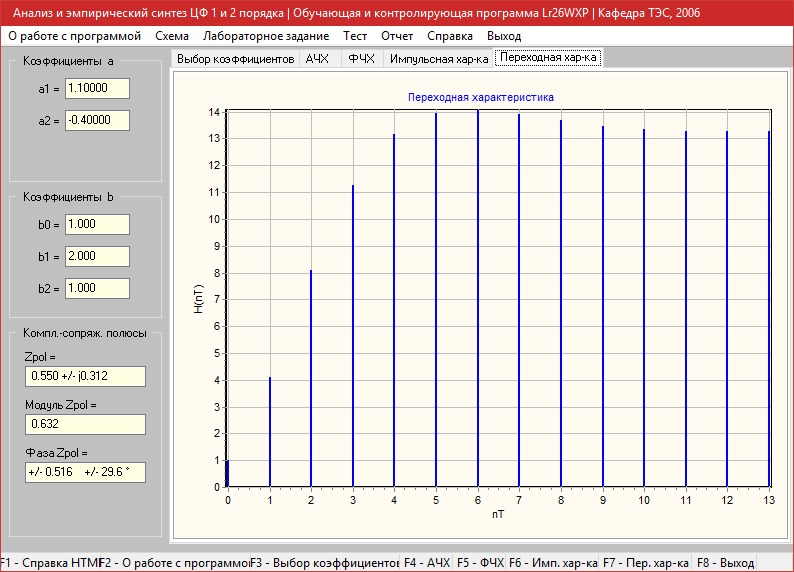
Переходная характеристика
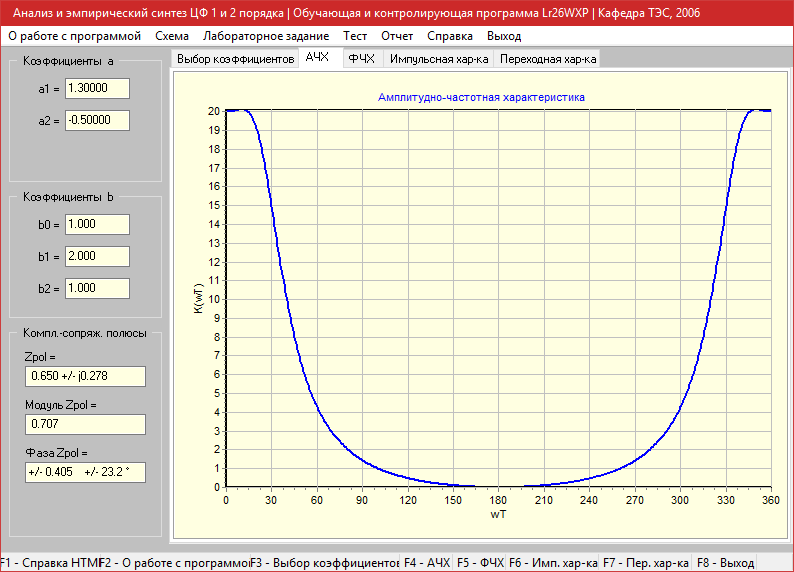
a1=1.3, a2=-0.5
Амплитудно-частотная характеристика
Фазо-частотная характеристика
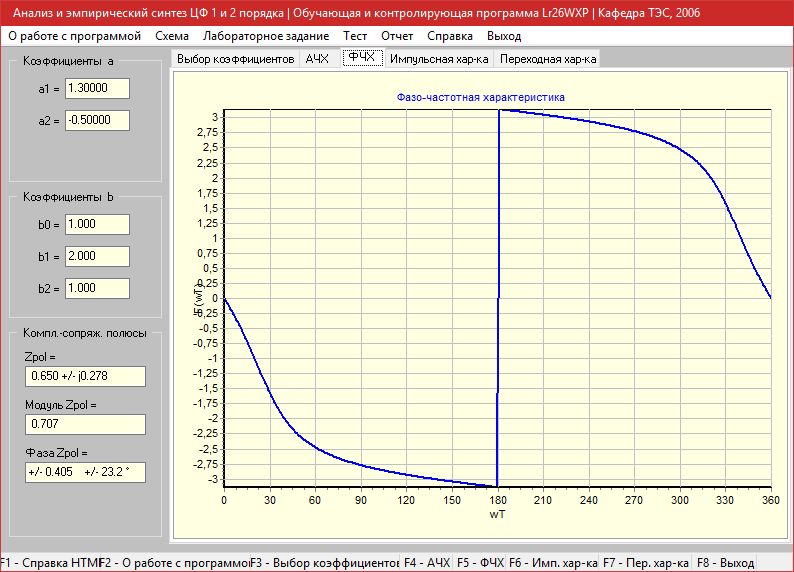
Импульсная характеристика
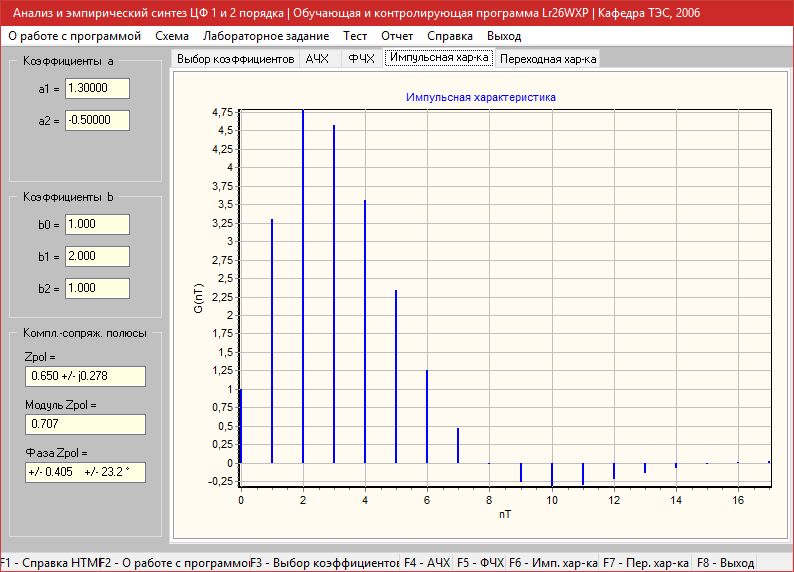
Переходная характеристика
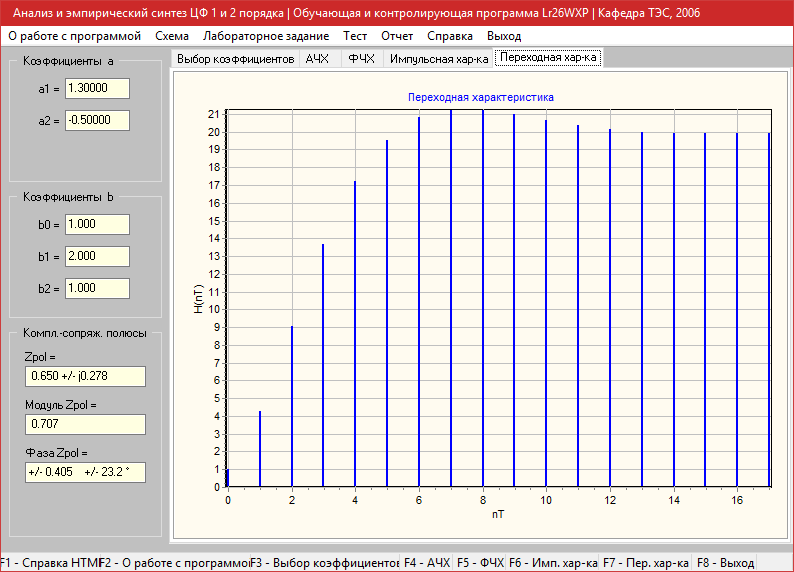
b1=-2, b2=1
a1=0.35, a2=-0.2
Амплитудно-частотная характеристика
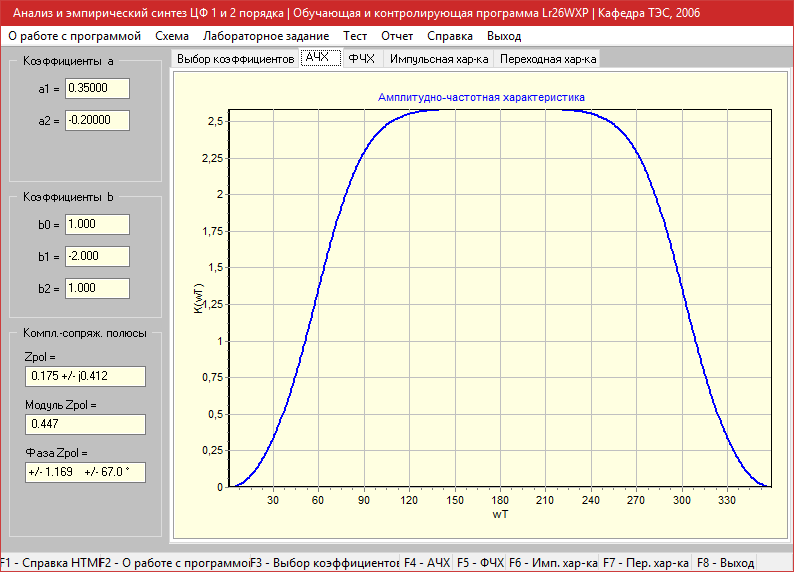
Фазо-частотная характеристика
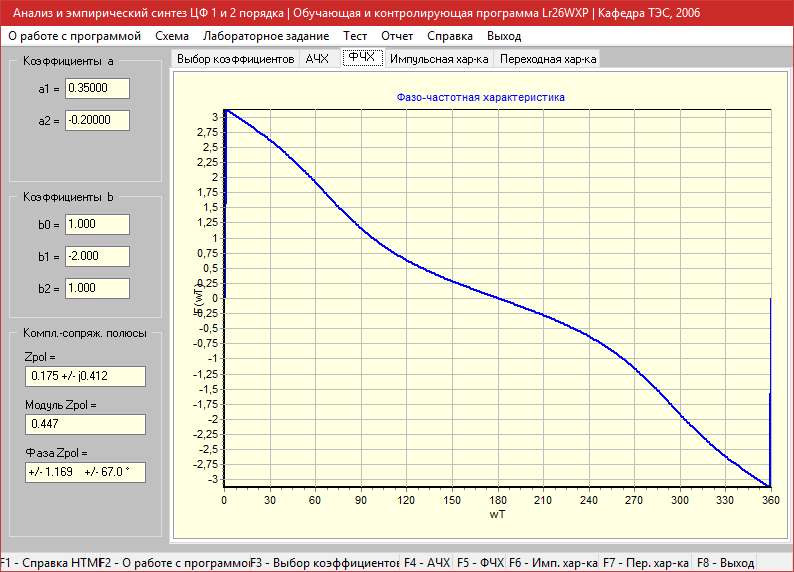
Импульсная характеристика
Переходная характеристика
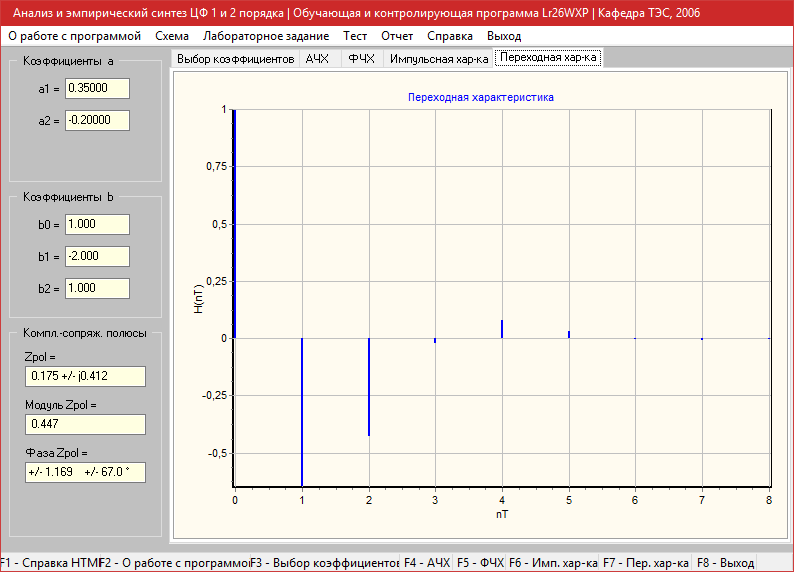
a1=0.8, a2=-0.3
Амплитудно-частотная характеристика
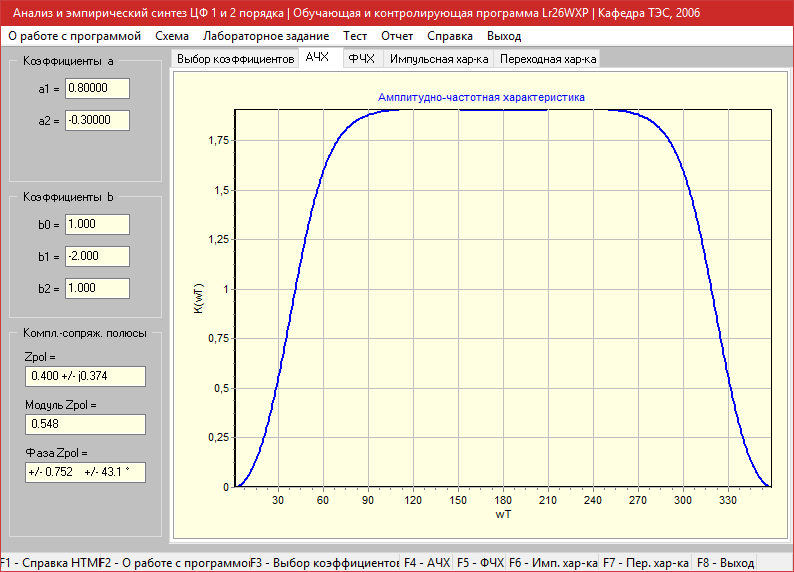
Фазо-частотная характеристика
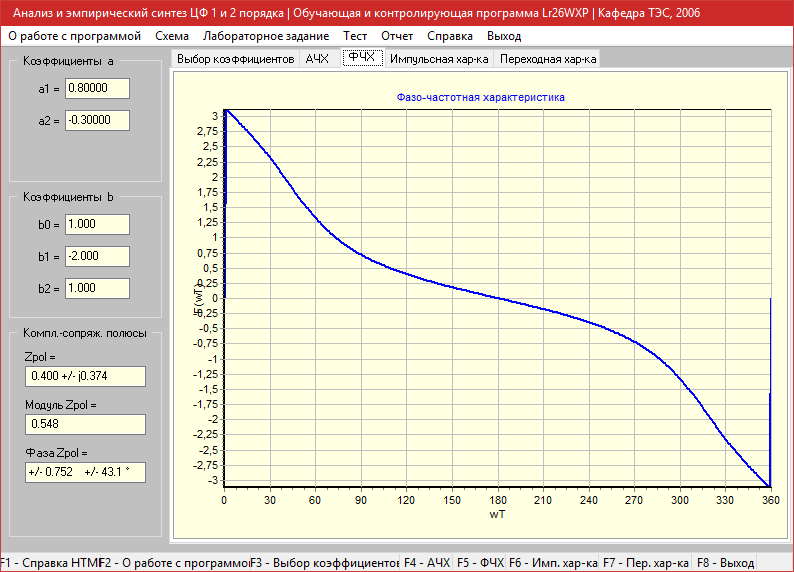
Импульсная характеристика
Переходная характеристика
a1=1.1, a2=-0.4
Амплитудно-частотная характеристика
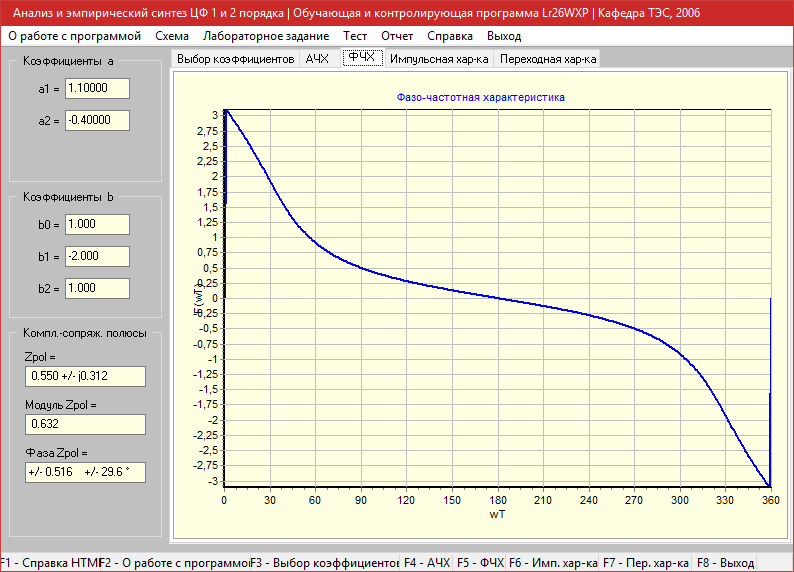
Фазо-частотная характеристика
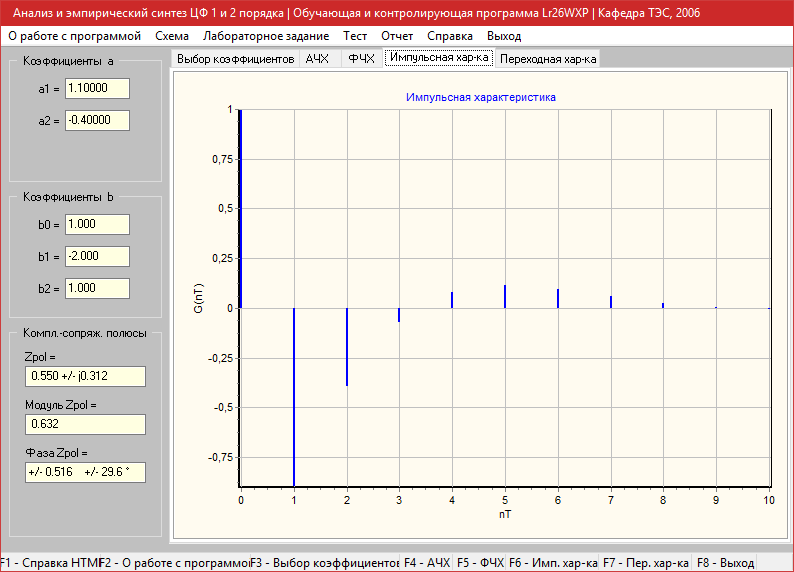
Импульсная характеристика
Переходная характеристика
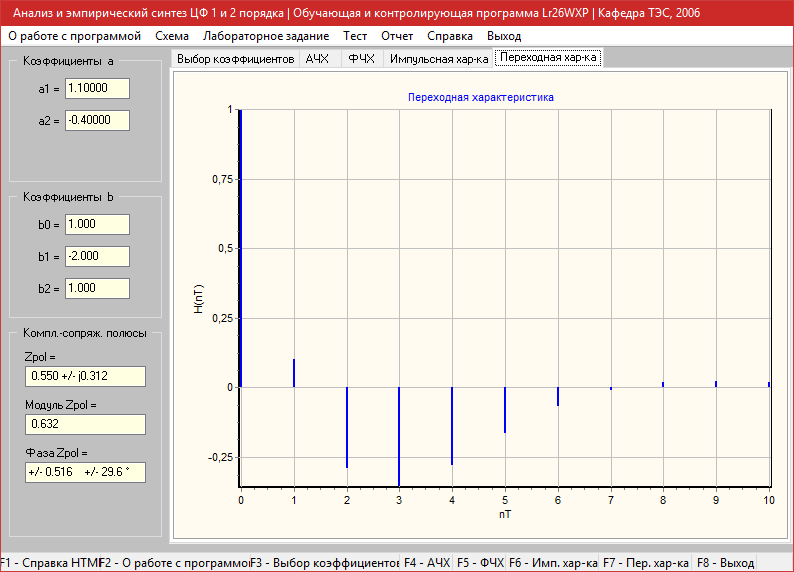
a1=1.3, a2=-0.5
Амплитудно-частотная характеристика
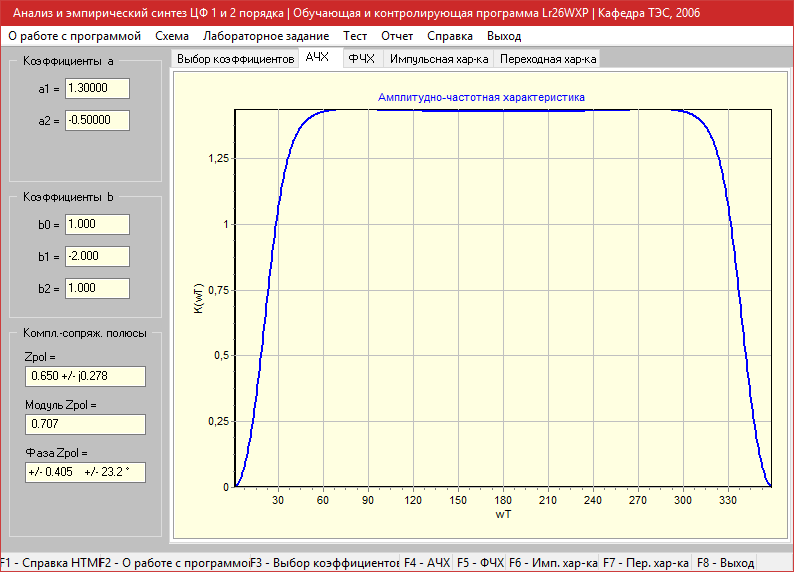
Фазо-частотная характеристика
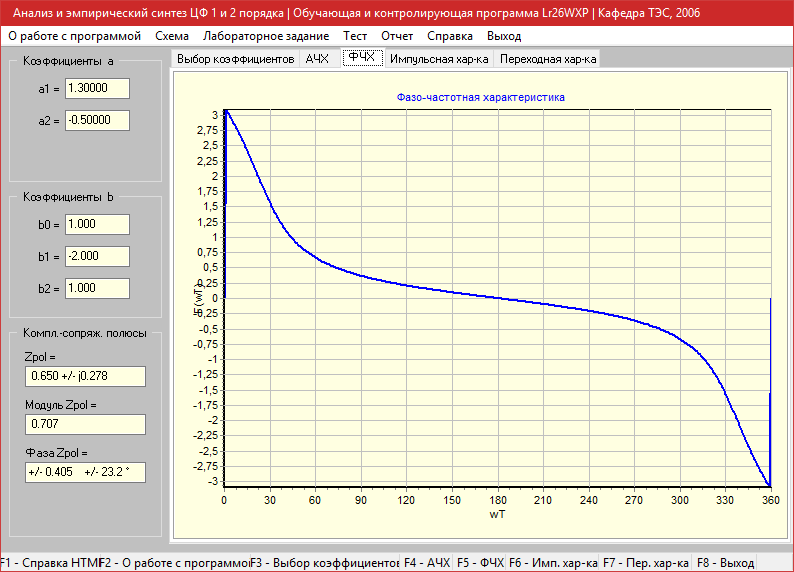
Импульсная характеристика
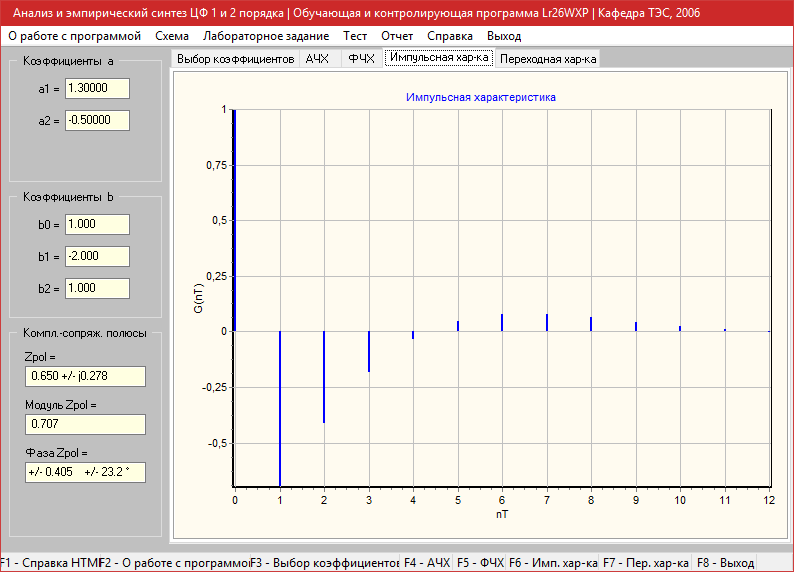
Переходная характеристика
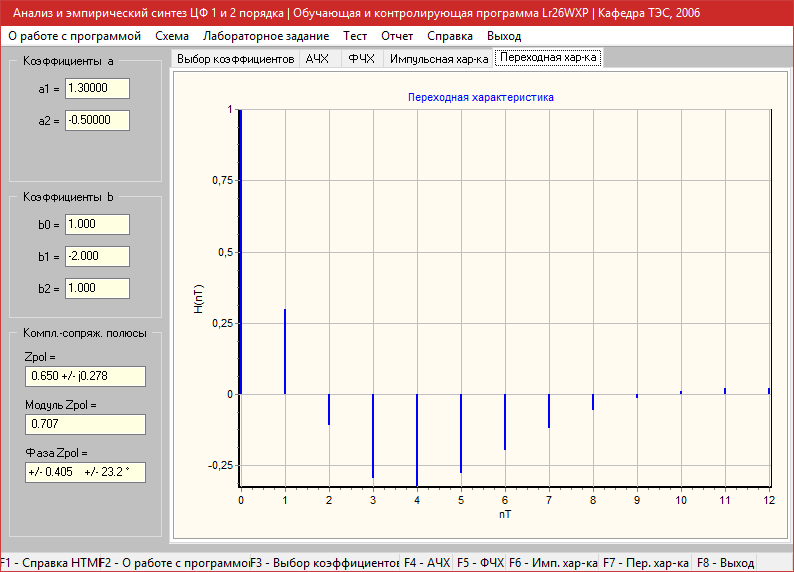
Эмпирический подбор коэффициентов
Фильтр: (a1=0.8,a2=-0.183 b0=1 b1=5 b2=1)
Амплитудно-частотная характеристика
Фазо-частотная характеристика
Импульсная характеристика
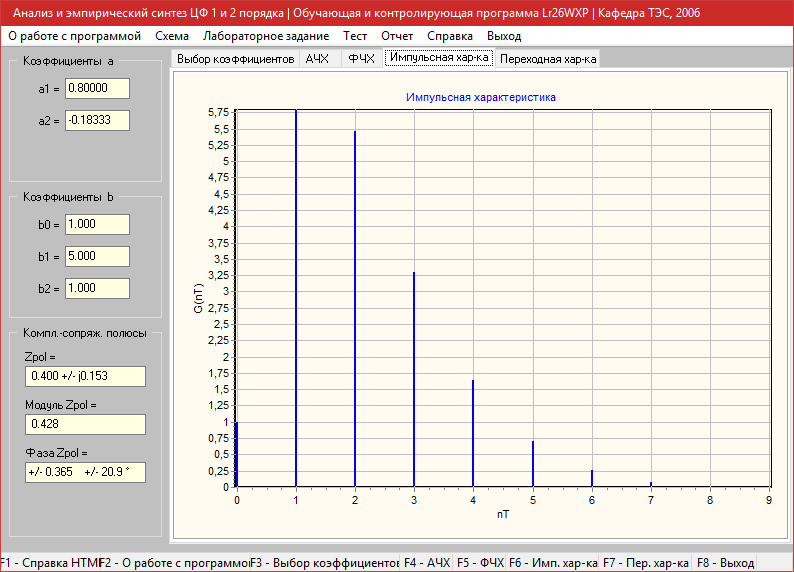
Переходная характеристика
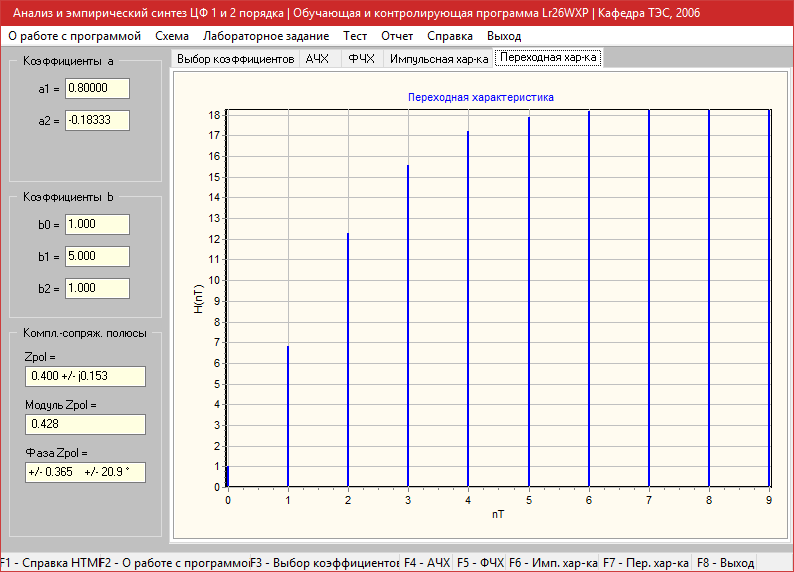
Фильтр: (a1=1,a2=-0.183 b0=1 b1=5 b2=1)
Амплитудно-частотная характеристика
Фазо-частотная характеристика
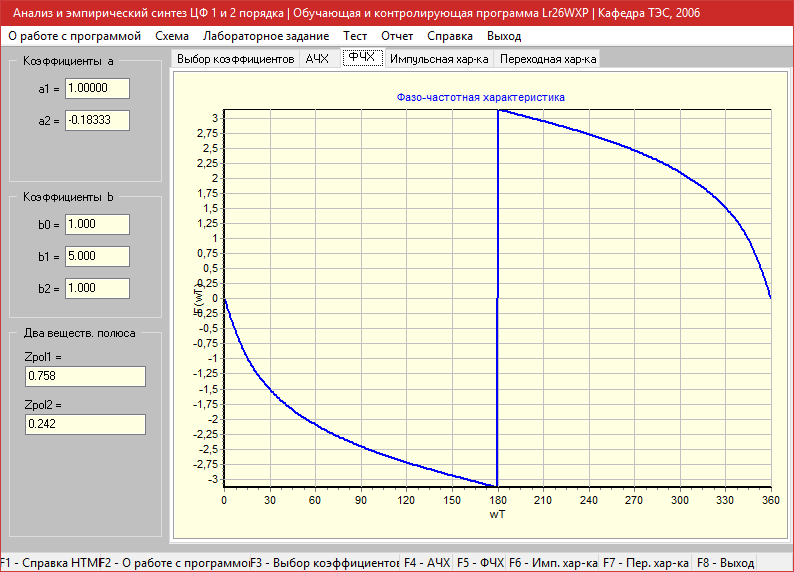
Импульсная характеристика
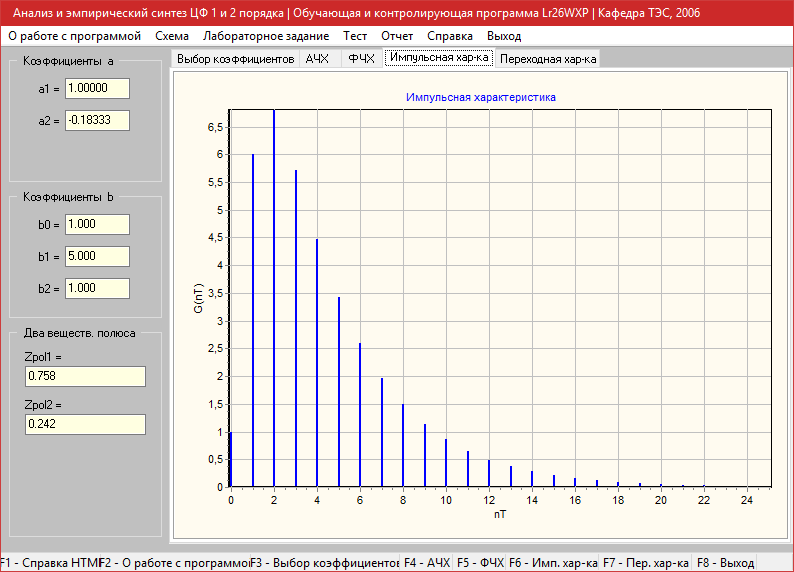
Переходная характеристика
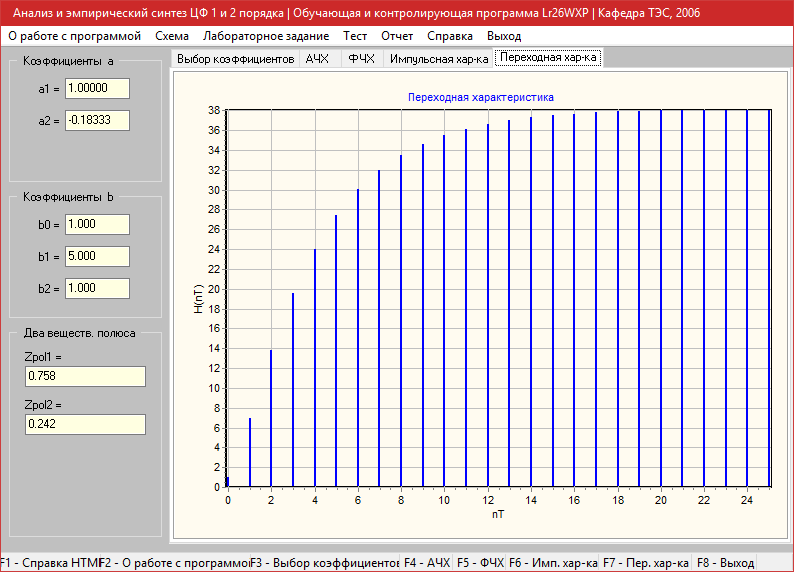
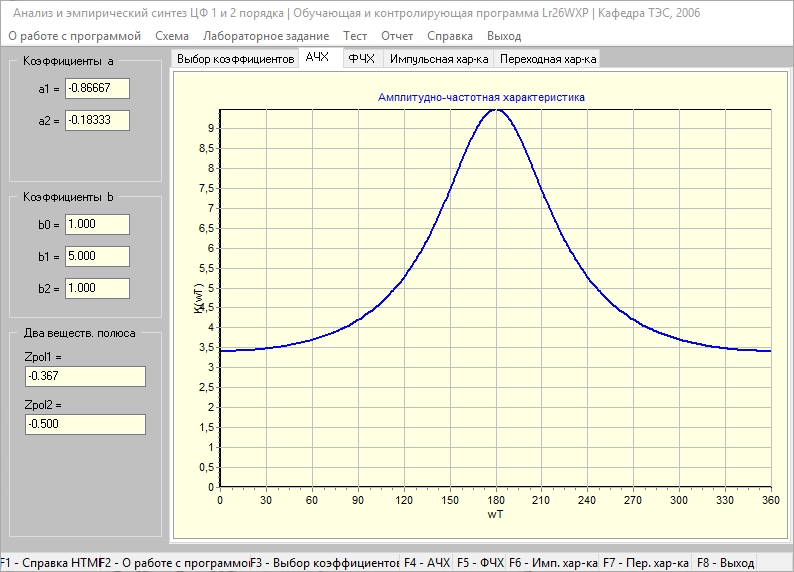
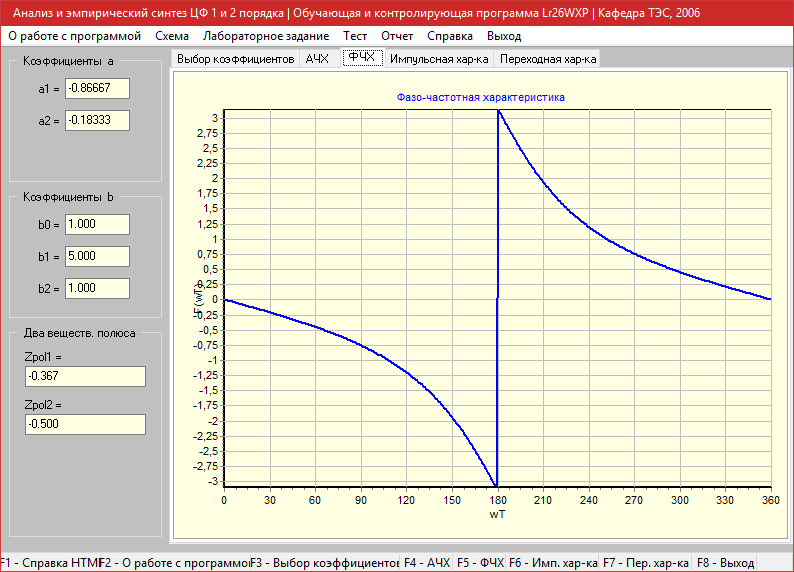
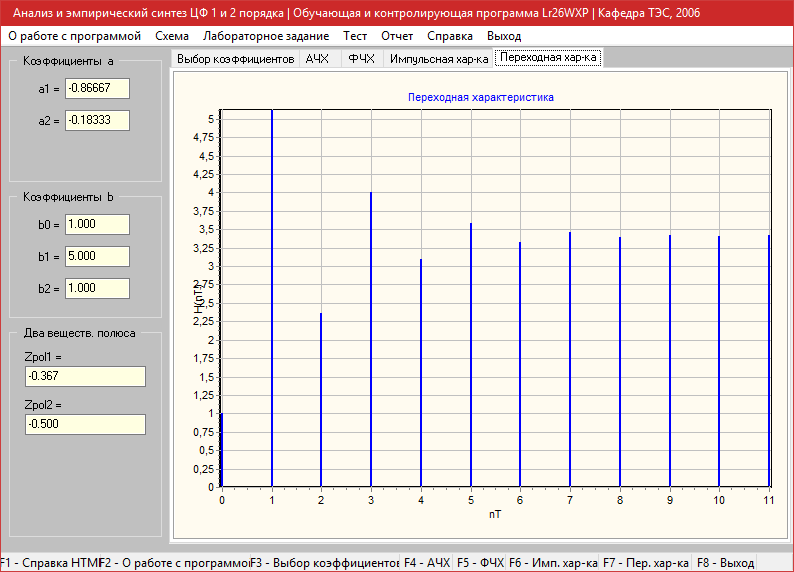
Фильтр: (a1=-0.866,a2=-0.183 b0=1 b1=5 b2=1)
Амплитудно-частотная характеристика
Фазо-частотная характеристика
Импульсная характеристика
Переходная характеристика
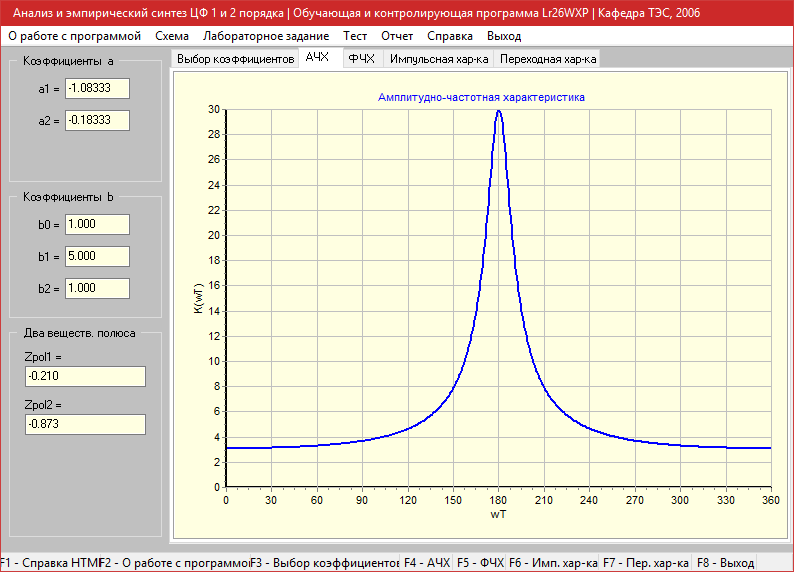
Фильтр: (a1=-1.083,a2=-0.183 b0=1 b1=5 b2=1)
Амплитудно-частотная характеристика
Фазо-частотная характеристика
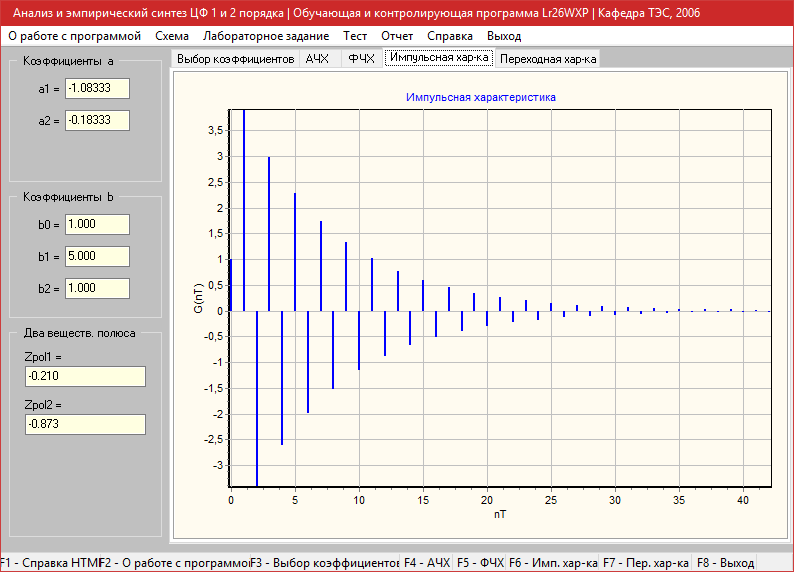
Импульсная характеристика
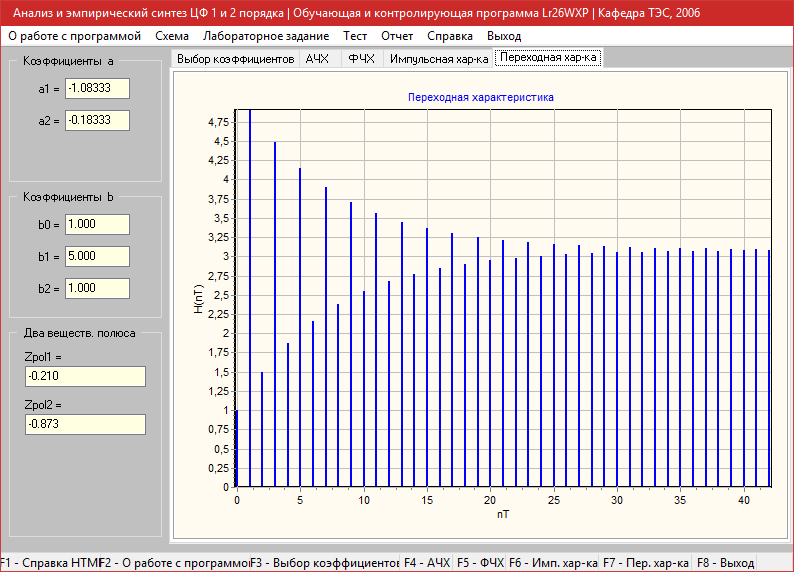
Переходная характеристика
Выводы по проделанной работе
При выполнении лабораторной работы были исследованы частотные и временные характеристики нерекурсивных и рекурсивных цифровых фильтров 1-го и 2-го порядка. В ходе эксперимента выяснилось, что характеристики ЦФ сильно зависят от значений коэффициентов b и a. Задавая определённые значения этих коэффициентов, можно влиять на характеристики ЦФ так, что его можно будет использовать для выделения сигнала на различных частотах (в качестве ФНЧ, ФВЧ и т.д.). Более того можно в значительной степени влиять на крутизну АЧХ.
4. Контрольный вопрос