
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ (МТУСИ)
Кафедра теории электрических цепей
Лабораторная работа № 12
«Временная дискретизация аналоговых сигналов»
Выполнил студент группы********** ___________________ ************
Проверил ____________________ *********
Москва 2004
Цель работы: с помощью программы Micro-Cap осуществить дискретизацию различных аналоговых сигналов.
Предварительный расчёт:
Провести дискретизацию аналогового сигнала с линейно изменяющимся напряжением, определяемого соотношением u1(t)=4t( B) на отрезке t[0;1] мс, при k=0,1,…,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми. Построим график данного дискретного сигнала.
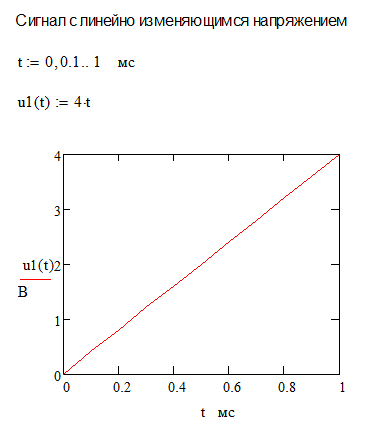
Провести дискретизацию аналогового единичного сигнала, определяемого соотношением u2(t)=1( B) на отрезке t[0;1] мс, при k=0,1,…,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми. Построим график данного дискретного сигнала.

![]()
Провести дискретизацию аналогового экспоненциального сигнала, определяемого соотношением u3(t)=exp( -4*10^(3)*t) на отрезке t[0;1] мс, при k=0,1,…,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми. Построим график данного дискретного сигнала.
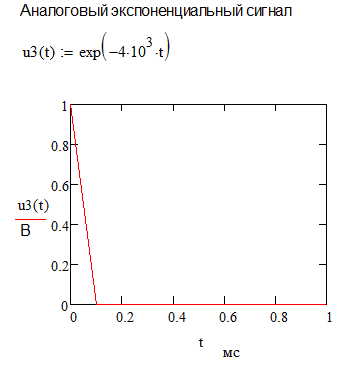
Провести дискретизацию аналогового двухполупериодного сигнала, определяемого соотношением u4(t)= cos(2*π*f*t) на отрезке t[0;1] мс, при k=0,1,…,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми. Построим график данного дискретного сигнала.

Провести дискретизацию аналогового косинусоидального сигнала, определяемого соотношением u5(t)= cos(2*π*f*t) на отрезке t[0;1] мс, при k=0,1,…,10 – номера отсчетов. Интервалы между моментами времени брать одинаковыми. Построим график данного дискретного сигнала.
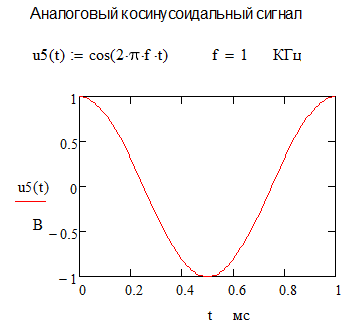
Предварительный расчет |
||||||
k |
tk |
U1(k) |
U2(k) |
U3(k) |
U4(k) |
U5(k) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0.1 |
0.0004 |
1 |
0.670 |
0.809 |
0.809 |
2 |
0.2 |
0.0008 |
1 |
0.449 |
0.309 |
0.309 |
3 |
0.3 |
0.0012 |
1 |
0.301 |
0.309 |
-0.309 |
4 |
0.4 |
0.0016 |
1 |
0.202 |
0.809 |
-0.809 |
5 |
0.5 |
0.0020 |
1 |
0.135 |
1 |
-1 |
6 |
0.6 |
0.0024 |
1 |
0.091 |
0.809 |
-0.809 |
7 |
0.7 |
0.0028 |
1 |
0.061 |
0.309 |
-0.309 |
8 |
0.8 |
0.0032 |
1 |
0.041 |
0.309 |
0.309 |
9 |
0.9 |
0.0036 |
1 |
0.027 |
0.809 |
0.809 |
10 |
1 |
0.0040 |
1 |
0.018 |
1 |
1 |
Эксперимент:
Дискретизация линейно изменяющегося напряжения:
4*t
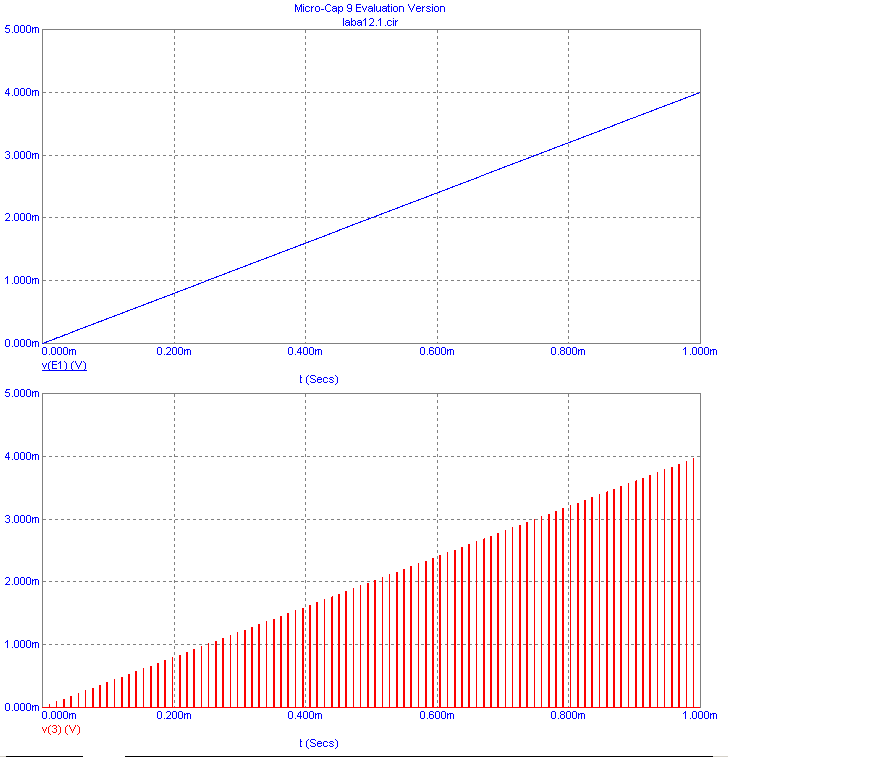
Дискретизация аналогового единичного сигнала:
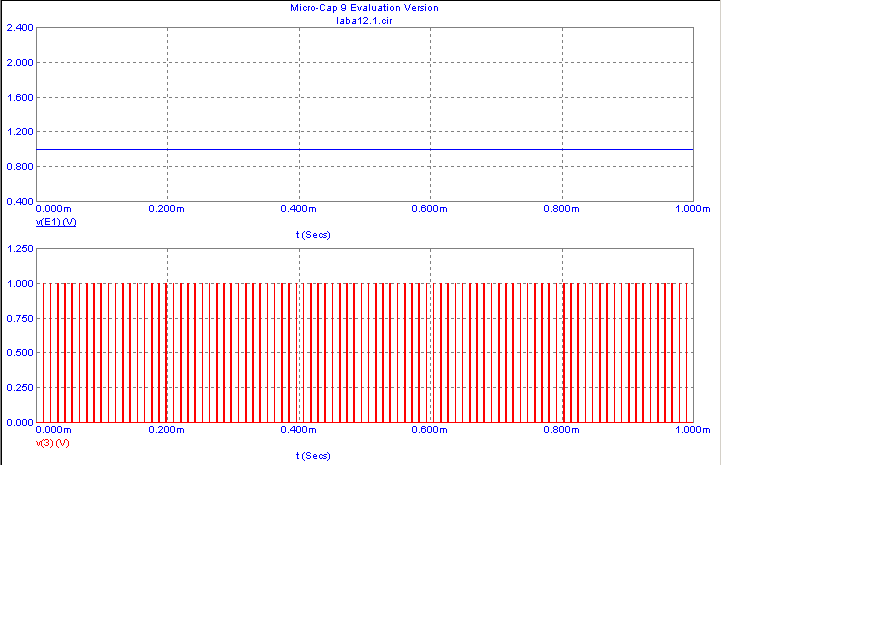
Дискретизация аналогового экспоненциального сигнала:
Exp(-4E3*t)
Дискретизация аналогового экспоненциального сигнала Exp(-4E3*t)
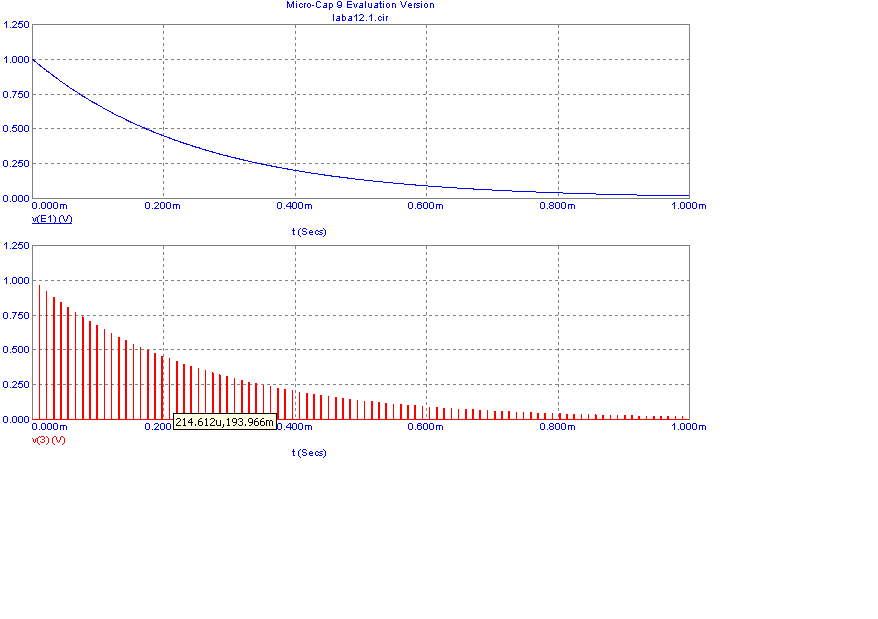
Дискретизация аналогового двухполупериодного сигнала:
Abs(cos(2*pi*t*1E3))
Дискретизация аналогового 2-хпериодного сигнала
Abs(cos(2*pi*t*1E3))
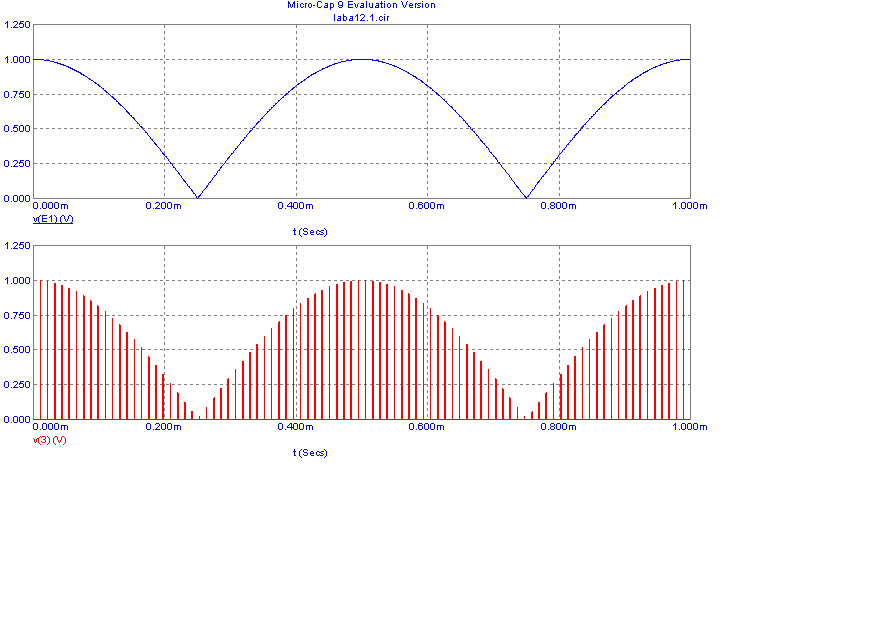
Дискретизация аналогового косинусоидального сигнала:
cos(2*pi*t*1E3)
Дискретизация аналогового косинусоидального сигнала
cos(2*pi*t*1E3)
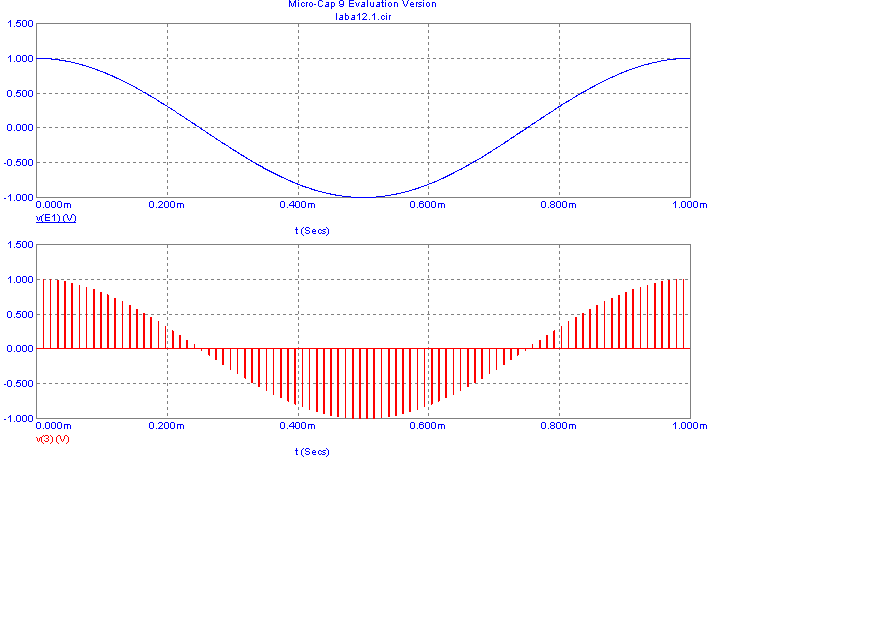
Эффект ложной частоты:
cos(2*pi*t*95E3)
Эффект ложной частоты
cos(2*pi*t*95E3)
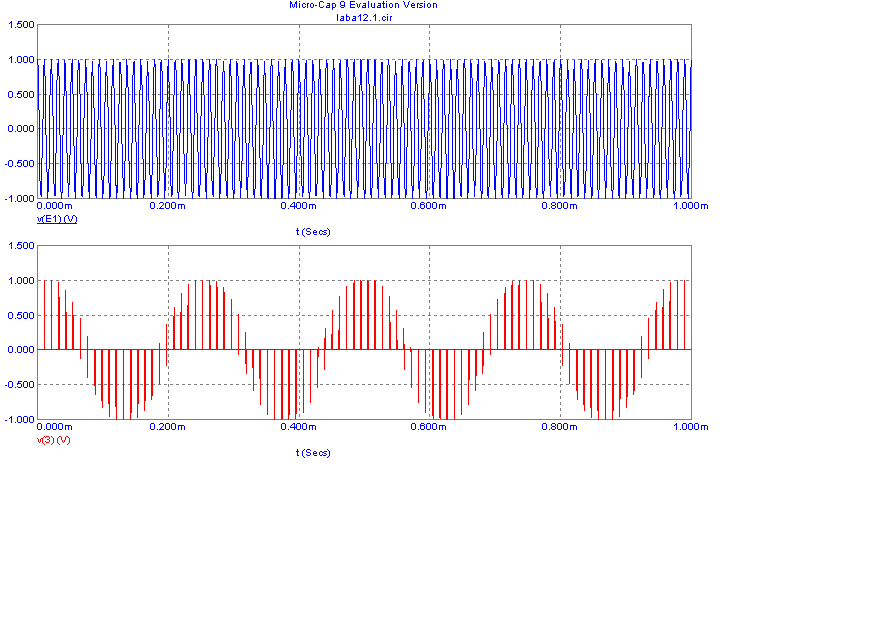
cos(2*pi*t*31E
cos(2*pi*t*31E3)
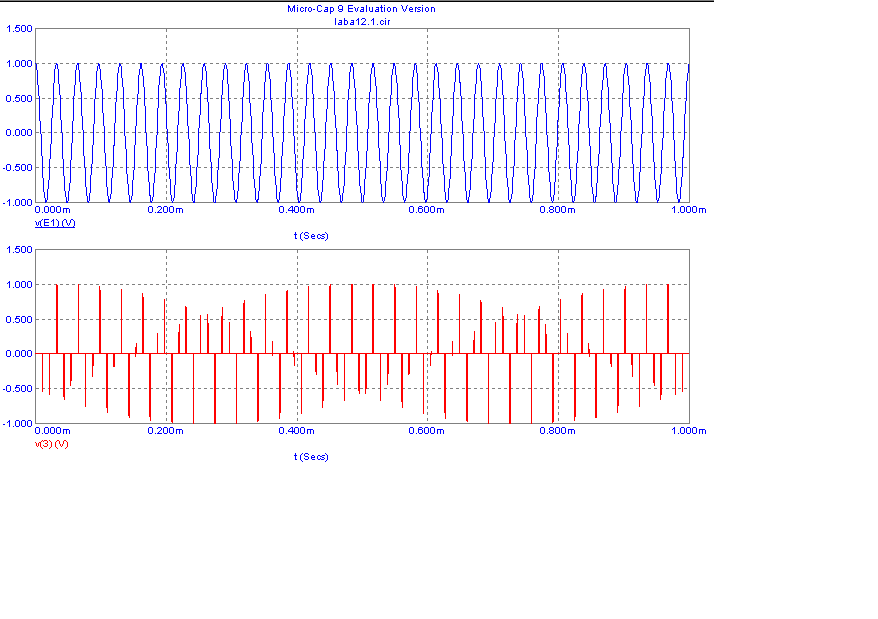
Вывод:
Исследовав цифровые логические элементы, были произведены предварительные расчеты, которые совпадают с расчетами, полученными в Micro-Cap. Это значит, что все составленные элементы были выполнены верно. А так же, осуществив дискретизацию различных аналоговых сигналов, мы убедились в верности теоремы Котельникова, которая гласит, что для дискретизации аналогового сигнала без потери информации частота отсчетов должна быть в два раза выше верхней граничной частоты спектра сигнала.
Вопросы для самопроверки:
1. Какие системы называются дискретными?
2. Как происходит преобразование аналоговых сигналов в дискретные?
3. Что называют отсчётами?
4. Какую величину называют тактовыми моментами?
5. Почему интервал дискретизации нельзя выбрать произвольным образом?
Ответы на вопросы:
1. Если система состоит исключительно из подсистем с дискретными состояниями, то и сама она может находиться лишь в конечном числе состояний, т. е. является системой с дискретными состояниями. Такие системы называются дискретными системами.
2. Получить дискретный сигнал из аналогового сигнала можно применив принцип импульсной амплитудной модуляцию Импульсный модулятор можно представить как умножитель с двумя входами и одним выходом. На первый вход импульсного модулятора подаётся аналоговый сигнал, подлежащий дискретизации. На второй вход последовательность коротких синхронизирующих импульсов, следующих во времени через равные промежутки времени Т (интервал дискретизации). На выходе образуется дискретный сигнал, величина выборок которого будет пропорциональна величине аналогового сигнала в точках отсчёта.
3. Отсчёты дискретного сигнала определены для дискретных значений независимой переменой времени и представляются последовательностью чисел.
4. Отсчёты и выборки.
5. Неправильный выбор частоты дискретизации аналоговых сигналов может привести к потери информации, поскольку дискретный сигнал не учитывает поведения аналогового сигнала в промежутках между отсчётами.
