ФEДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное

Бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

Кафедра теории электрических цепей

Лабораторная работа №17

«Исследование на ЭВМ резонансных явлений в пассивном и активном параллельном колебательном контуре»

Выполнила студент группы _______________ фио

Проверил доц. кафедры ТЭЦ ______________ фио

Москва 0000

Цель работы:

С помощью программы Mirco-Cap получить входные и передаточные параллельного колебательного контура при различных добротностях.

Расчетные формулы:

Y_вх=(1/R)+j(ωC-(1/ωL)), - комплексное входная проводимость контура

Резонансная частота контура

f_p=1/(2π )

Характеристическое сопротивление

p=

Добротность

Q=R/p= f_p/П

Нижняя граничная частота

ω ₁=(-1/2RC)+sqrt((1/2RC)^2+1/LC)

f₁=ω₁/2π

Верхняя граничная частота

ω₂=(-1/2RC)+sqrt((1/2RC)^2+1/LC)

f₂=ω₂/2π

Абсолютная полоса пропускания

П= f₂- f₁

Комплексное входное сопротивление

Z_вх=1/(1/R)+j(ωC-(1/ωL))=Z(ω)e^jϕ(ω)

Модуль комплексного входного сопротивления при условии, что меняется только частота источника напряжения

Z(ω)=1/sqrt(1/((1/R)^2)+(ωC-(1/ωL))^2)

Фаза входного сопротивления в градусах

ϕ(ω)= arctg[(ωC-(1/ωL))R]

Комплексные токи

I=U₁/ Z_вх, I_R=U₁/R, I_L=U₁/jωL, I_C=U₁/(-j/ωC)

Добротность Q последовательного контура при помощи резонансных кривых

Q=f₀/f₂-f₁

Комплексное входное сопротивление

Z_вх = ((R+jωL)(-j/ωC))/ (R+j(ωC-(1/ωL))

Модуль комплексного входного сопротивления при резонансе

Z(f_p1)=RQ²

Резонансная частота контура

f_p1=ω/2π

Предватрительный расчет:

По предварительному расчету R=14кОм, fр=5 кГц,C=30*10^-9 Ф ,L=0,038 Гн							Получено экспериментально
p, Ом	Q	f1, кГц	f2, кГц	П, кГц	Z(fp), Ом	f0, кГц		fp, Гц	Z(fp), Ом	f1, кГц	f2, кГц	П, кГц	Q
1601	18,5	4,86	5,13	0,24	14000	5		5000	14000	4,86	5,13	0,24	18,5

По предварительному расчету C2=30*10^-9 Ф, L=0,038Гн				Получено экспериментально
Q	R, Ом	fp1, кГц	Z(fp), кОм	fp1, кГц	Z(fp), кОм
2	530	5	2,589	5	2,589
100	10	5	125,1	5	125,1

Зависимость модуля входного сопротивления от частоты

Вывод: Модуль входного сопротивление максимален на частоте резонанса, так как на этой частоте индуктивное сопротивление равно емкостному

Теоретическая зависимость фазы входного сопротивления

от частоты

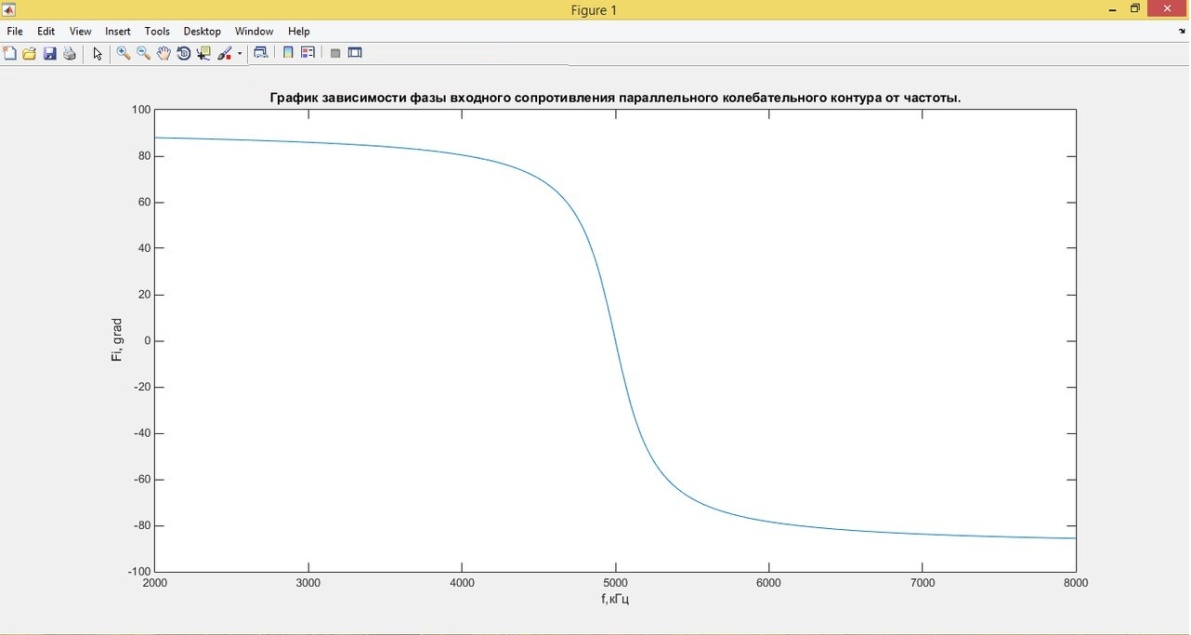
Вывод: График имеет перегиб в точке: f=f_R, ϕ=0, так как на частоте резонанса индуктивное сопротивление равно емкостному сопротивлению.

Теоретический график зависимостей модулей входного тока,модуля тока в резисторе, модуля тока в катушке и модуля тока в конденсаторе

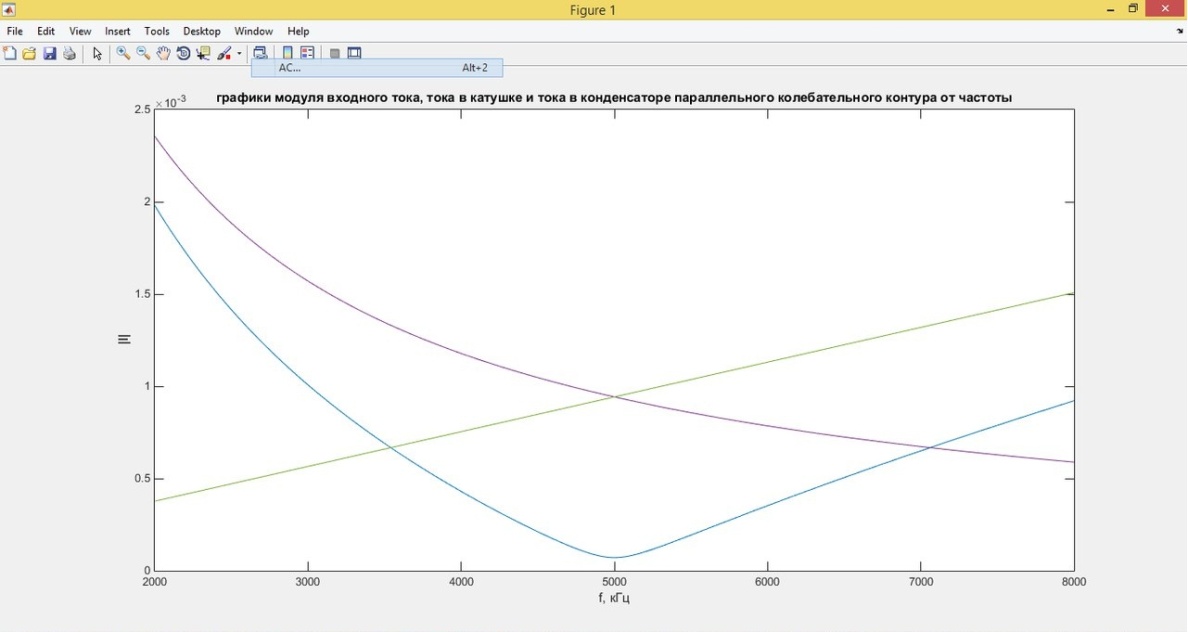
Вывод: Из графика мы видим, что модуль входного тока принимает наименьшее значение при резонансной частоте, т.к. при частоте резонанса индуктивное сопротивление равно емкостному, а реактивные токи находятся в противофазе и компенсируют друг друга.

Графики и выводы:

Зависимость модуля входного сопротивления от частоты

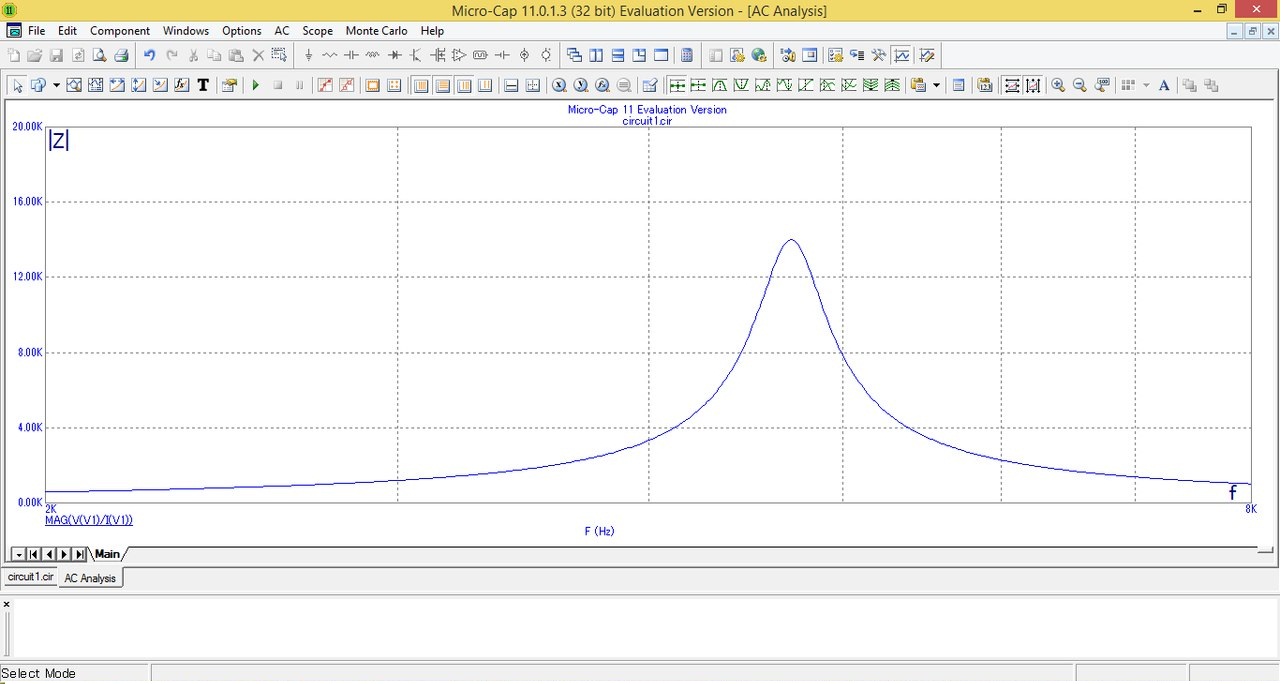
Вывод: Модуль входного сопротивление максимален на частоте резонанса, так как на этой частоте индуктивное сопротивление равно емкостному

Зависимость фазы входного сопротивления от частоты

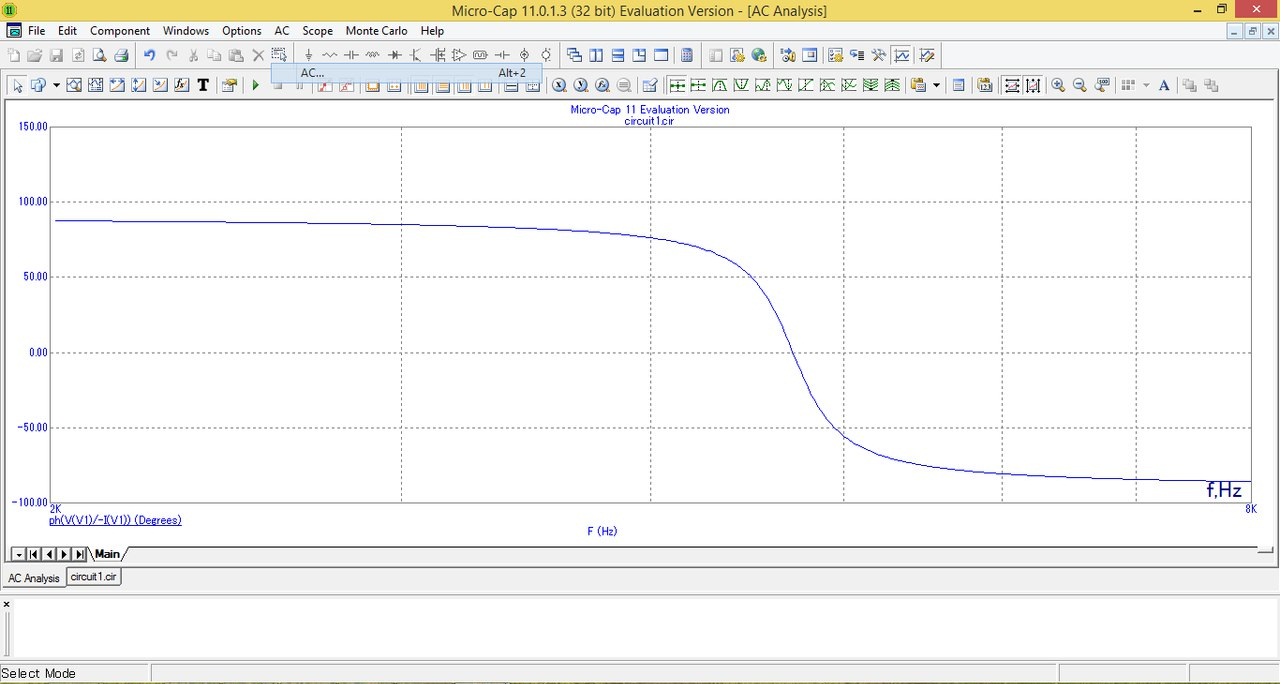
Вывод: График имеет перегиб в точке: f=f_R, ϕ=0, так как на частоте резонанса индуктивное сопротивление равно емкостному сопротивлению.

График зависимостей модулей входного тока, модуля тока в резисторе, модуля тока в катушке и модуля тока в конденсаторе

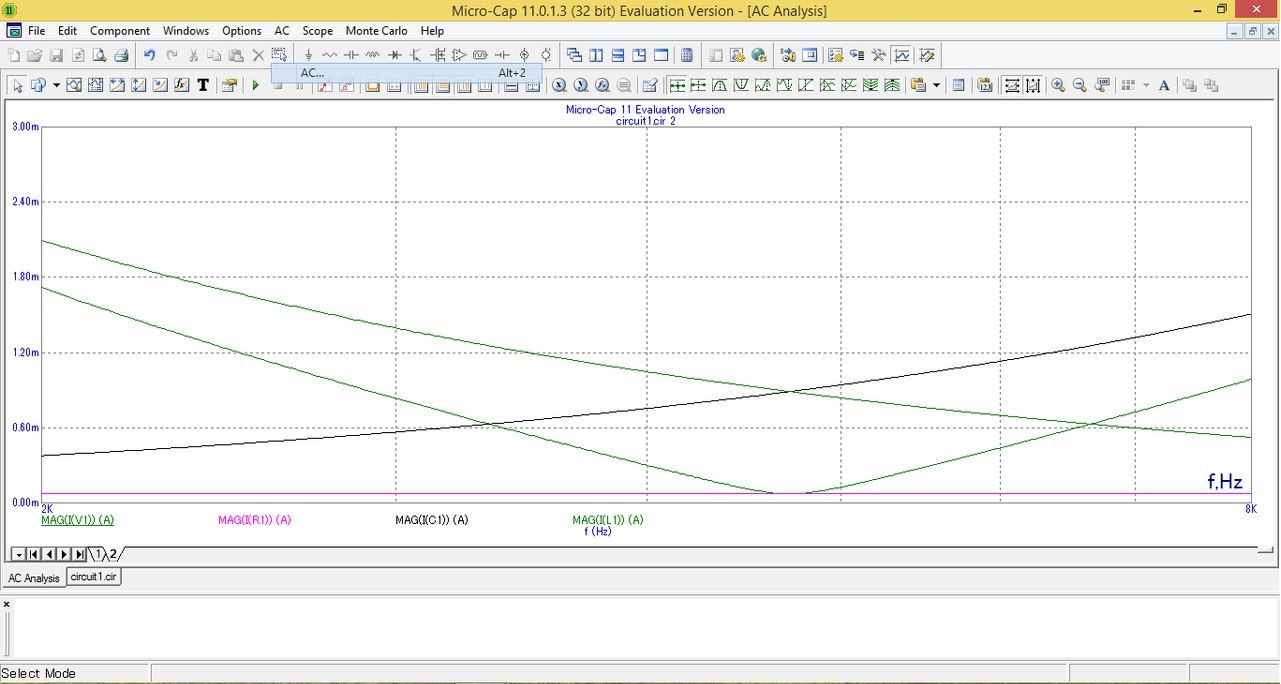
Вывод: Из графика мы видим, что модуль входного тока принимает наименьшее значение при резонансной частоте, т.к. при частоте резонанса индуктивное сопротивление равно емкостному, а реактивные токи находятся в противофазе и компенсируют друг друга.

Частотные характеристики контуров первого типа для значений добротности 2(первый график),100(второй график)

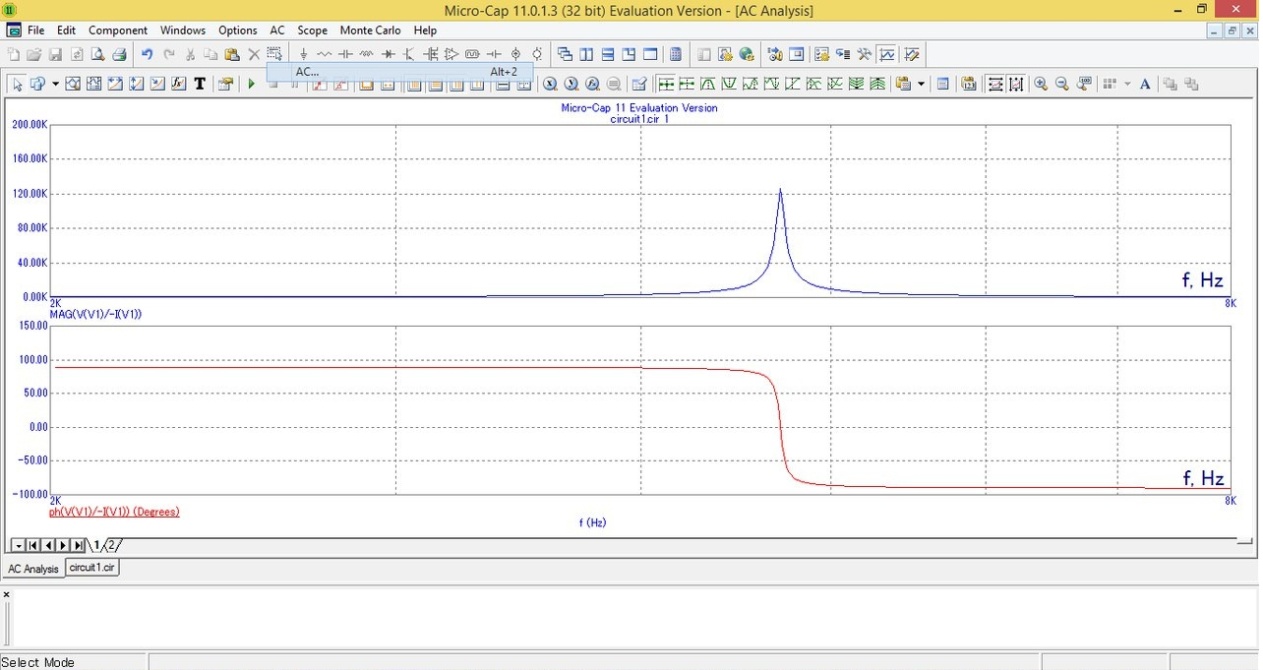
Вывод: Из графиков мы видим, что при более высокой добротности полоса пропускания уменьшается, а ФЧХ имеет более крутой перегиб, в следствие того, что активное сопротивление уменьшается.

График зависимостей модулей входного тока,модуля тока в резисторе, модуля тока в катушке и модуля тока в конденсаторе

Вывод: Из графика мы видим, что модуль входного тока принимает наименьшее значение при резонансной частоте, т.к. при частоте резонанса индуктивное сопротивление равно емкостному, а реактивные токи находятся в противофазе и компенсируют друг друга.

Контрольные Вопросы:

1. Почему резонанс в параллельном пассивном колебательном контуре называется резонансом токов?

Ответ: Резонанс в параллельном колебательном контуре называется резонансом токов ,потому что при резонансной частоте индуктивное сопротивление равно емкостному сопротивлению, а как следствие токи в цепях с индуктивностью и емкостью равны и находятся в противофазе. Поэтому ток в цепи имеет только активную составляющую.

2. Как рассчитывается резонансная частота параллельного колебательного контура?

Ответ: f_p=1/(2π )

3. Что такое добротность параллельного пассивного колебательного контура?

Ответ: Добротность – характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

4. Что такое полоса пропускания параллельного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

Ответ: Полоса пропускания параллельного пассивного колебательного контура это диапазон частот, который определяют по резонансной кривой на уровне 0,7 от максимального значения напряжения,соответстующей резонансной частоте.

Способы расчета: 1) Графический способ

Это способ, при котором полосу пропускания определяют непосредственно по графику.

2) Аналитический способ

Способ, при котором рассчитывают нижнюю и верхнюю граничные частоты,а потом из верхней вычитают нижнюю.

5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ параллельного пассивного колебательного контура.

Ответ:

Z_KK(jω)= = =

Так как вблизи от резонанса L , , получим окончательное выражение сопротивления паралленьго колебательного контура

= =

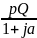
АЧХ: Z_ВХ(ω)=

ФЧХ: ϕ_Z(ω)=arg(z)