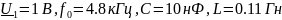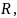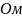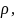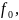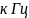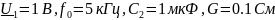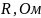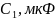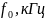ФEДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ

Ордена Трудового Красного Знамени федеральное государственное

Бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

Кафедра теории электрических цепей

Лабораторная работа №16

Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре

Выполнила студент группы _______________ фио

Проверил доц. кафедры ТЭЦ ______________ фио

Москва 0000

1. Цель работы: С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.

2. Расчетные формулы:

3. Выполнение работы:

По предварительному расчету										Получено эксперементально
160	3315.7	4.55	4685.6		4917.22	232.2	0.006	4.8	4796		0.006	4684	4916	232	20.7
640	3315.7	2.28	4359		5285.63	926.63	0.0015	4.8	4796		0.0015	4358	5285	927	5.17
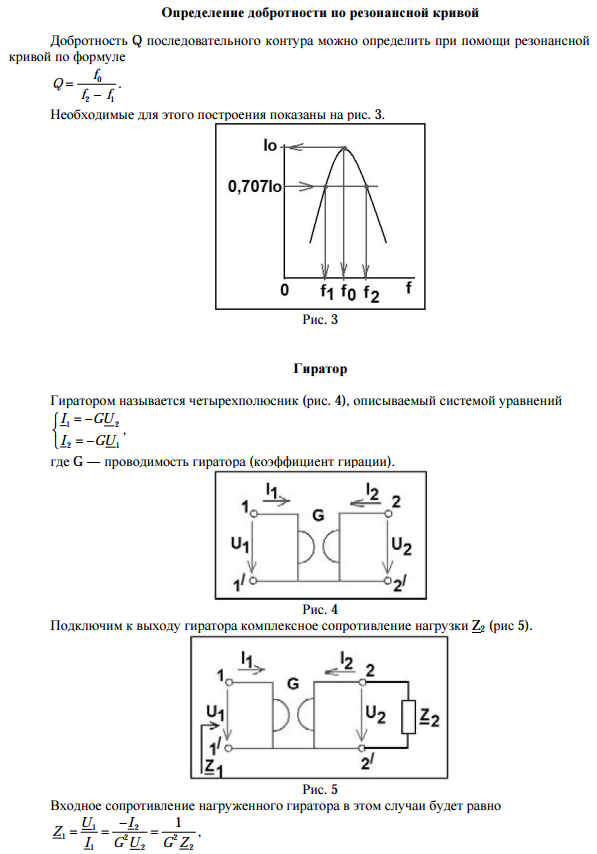
Гиратор
По предварительному расчету										Получено эксперементально
0.1				10.14					50.00204’b

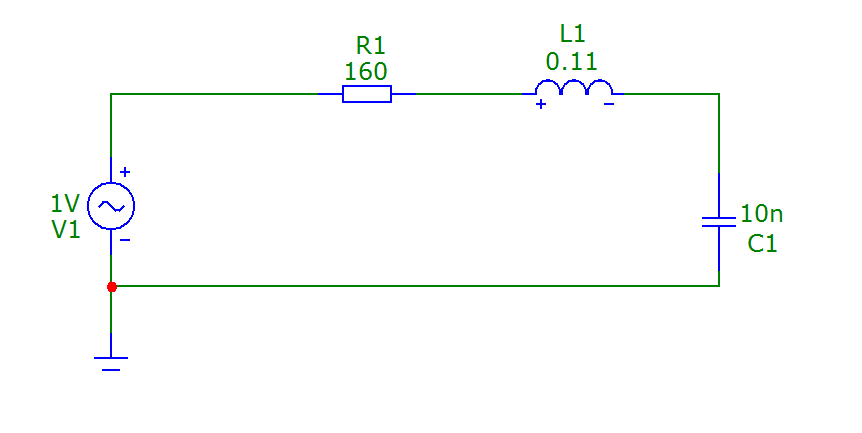
Рисунок 1 – Схема пассивного последовательного колебательного контура

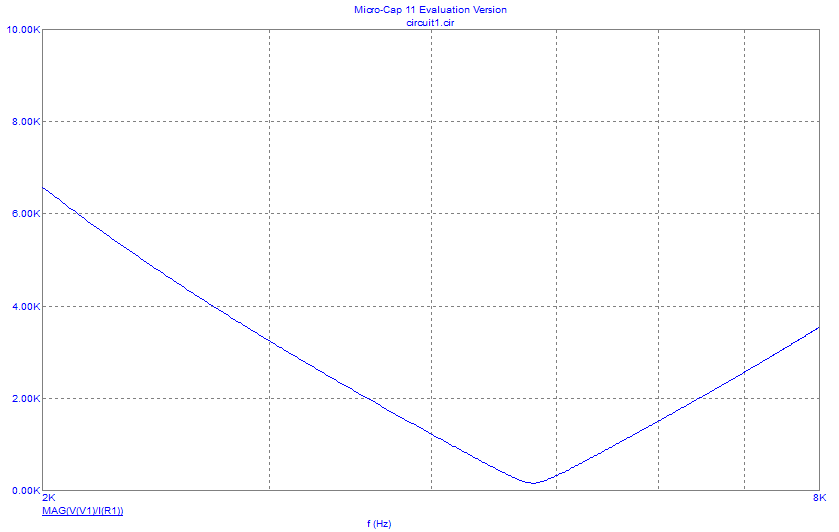
Рисунок 2– Экспериментальная зависимость модуля входного сопротивления от частоты

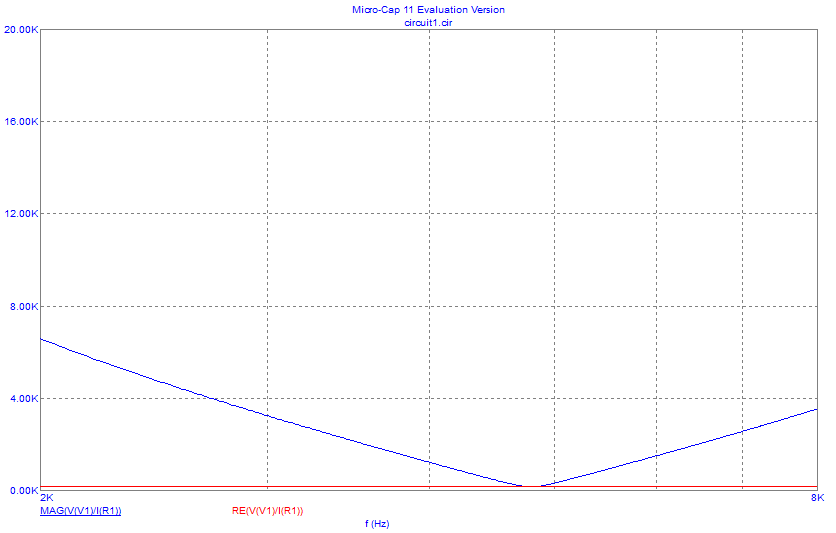
Рисунок 3– Экспериментальная зависимость модуля входного сопротивления от частоты

и зависимость действительной части входного сопротивления

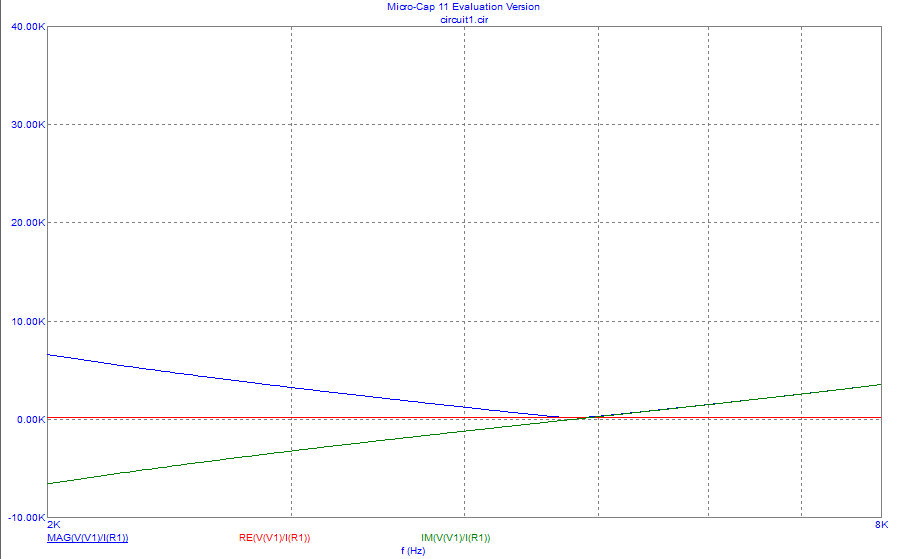
Рисунок 4 – Экспериментальная зависимость модуля входного сопротивления от частоты, зависимость действительной части входного сопротивления, зависимость мнимой части входного сопротивления

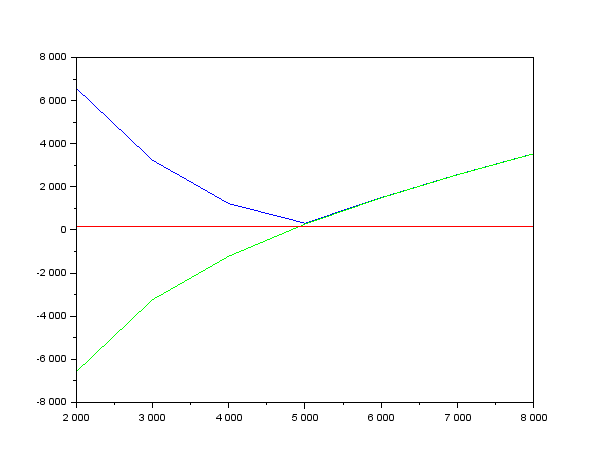
Рисунок 5 – Теоретическая зависимость модуля входного сопротивления от частоты (синий), зависимость действительной части входного сопротивления (красный), зависимость мнимой части входного сопротивления (зеленый), при 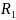=160 Ом

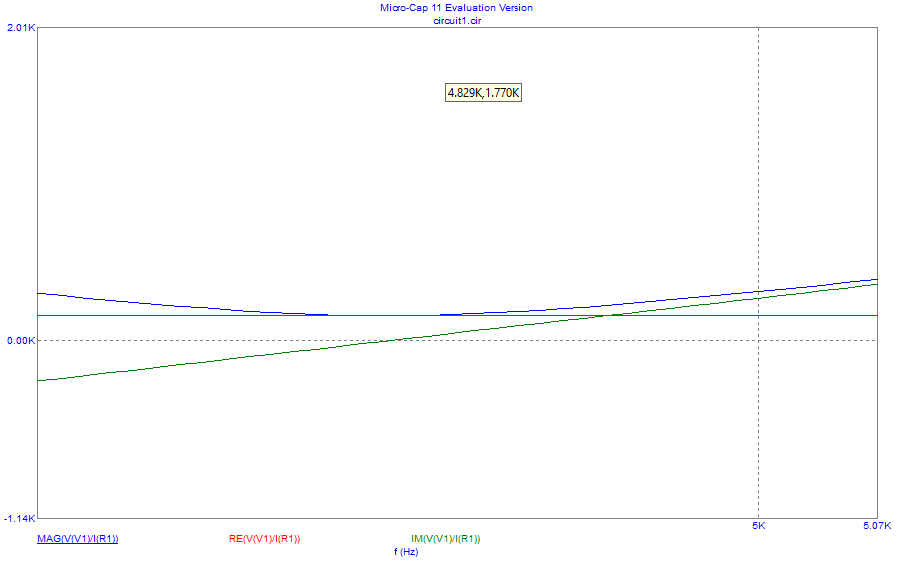
Рисунок 6– Экспериментальная зависимость модуля входного сопротивления от частоты (синий), зависимость действительной части входного сопротивления (красный), зависимость мнимой части входного сопротивления (зеленый), при =160 Ом

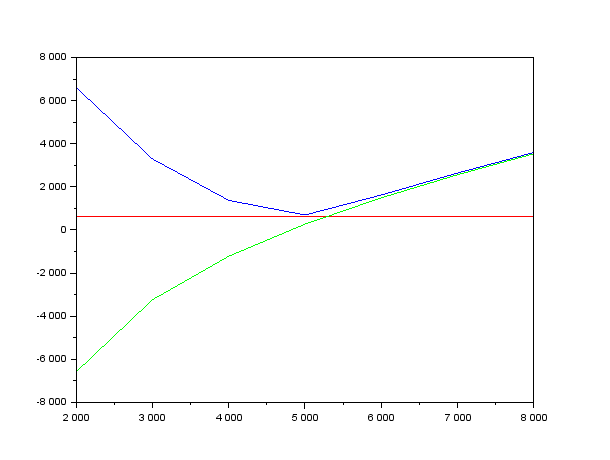
Рисунок 7 – Теоретическая зависимость модуля входного сопротивления от частоты (синий), зависимость действительной части входного сопротивления (красный), зависимость мнимой части входного сопротивления (зеленый), при 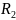=640 Ом

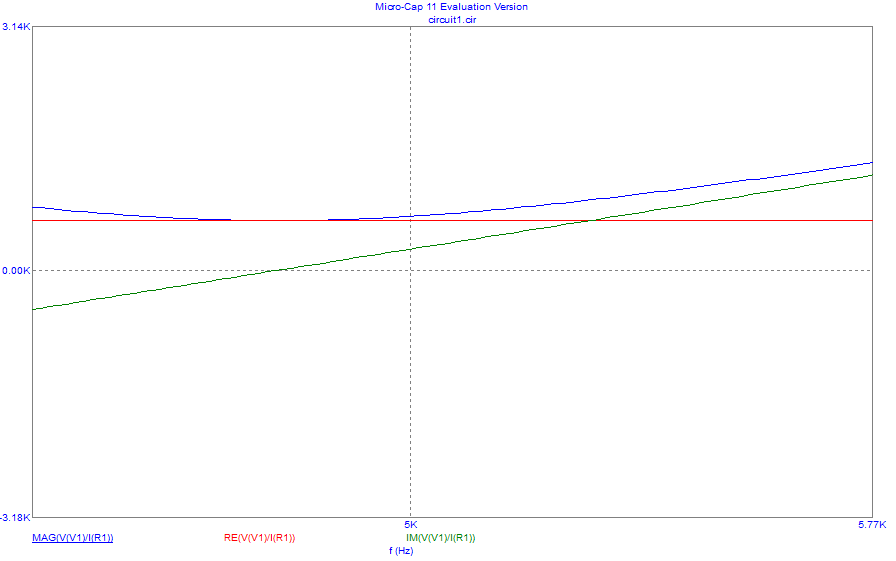
Рисунок 8– Экспериментальная зависимость модуля входного сопротивления от частоты (синий), зависимость действительной части входного сопротивления (красный), зависимость мнимой части входного сопротивления (зеленый), при =640 Ом

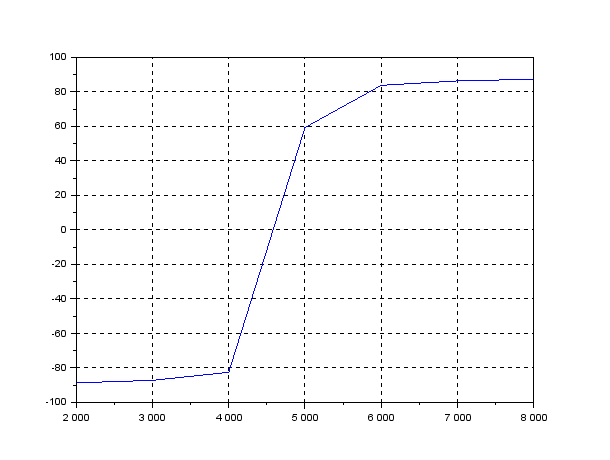
Рисунок 9– Теоретическая зависимость фазы входного сопротивления от частоты при =160 Ом

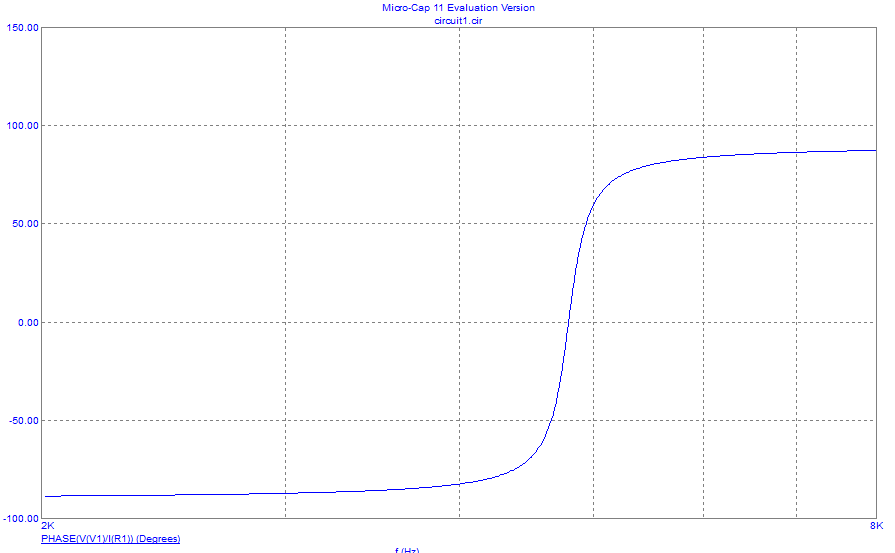
Рисунок 10– Экспериментальная зависимость фазы входного сопротивления от частоты при =160 Ом

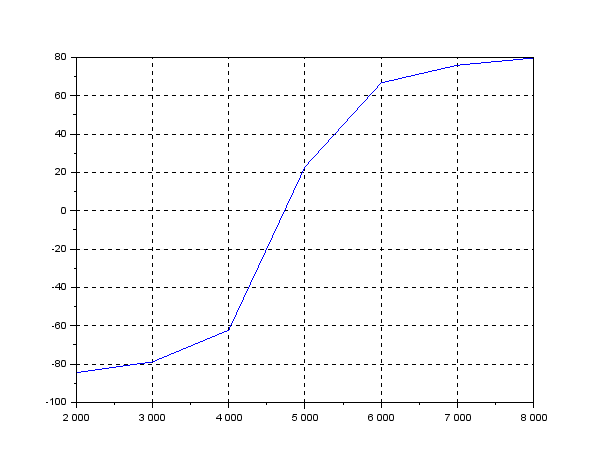
Рисунок 11 – Теоретическая зависимость фазы входного сопротивления от частоты при =640 Ом

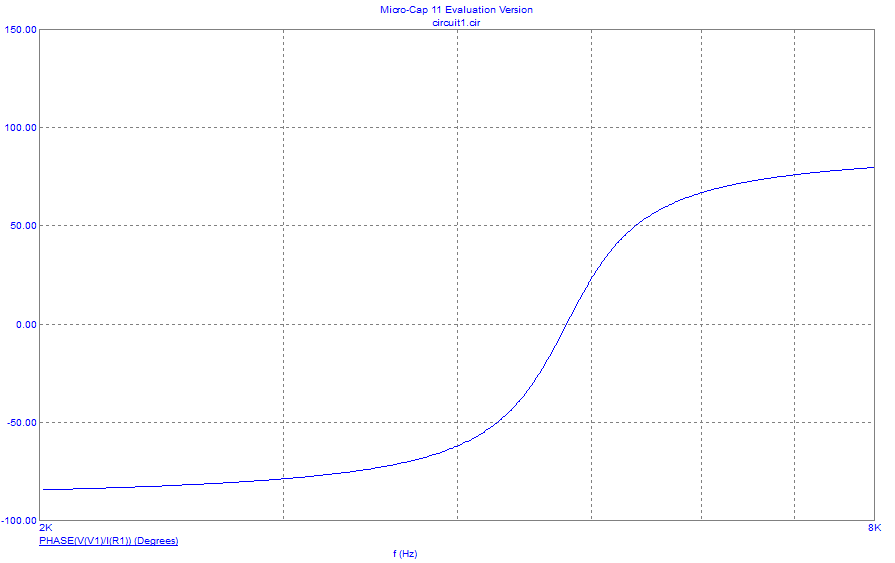
Рисунок 12 – Экспериментальная зависимость фазы входного сопротивления от частоты при =640 Ом

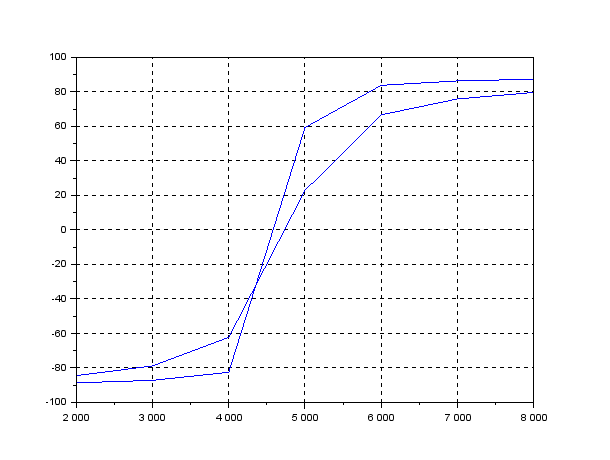
Рисунок 13 – Теоретическая зависимость фазы входного сопротивления от частоты

при =160 Ом и =640 Ом на одном графике

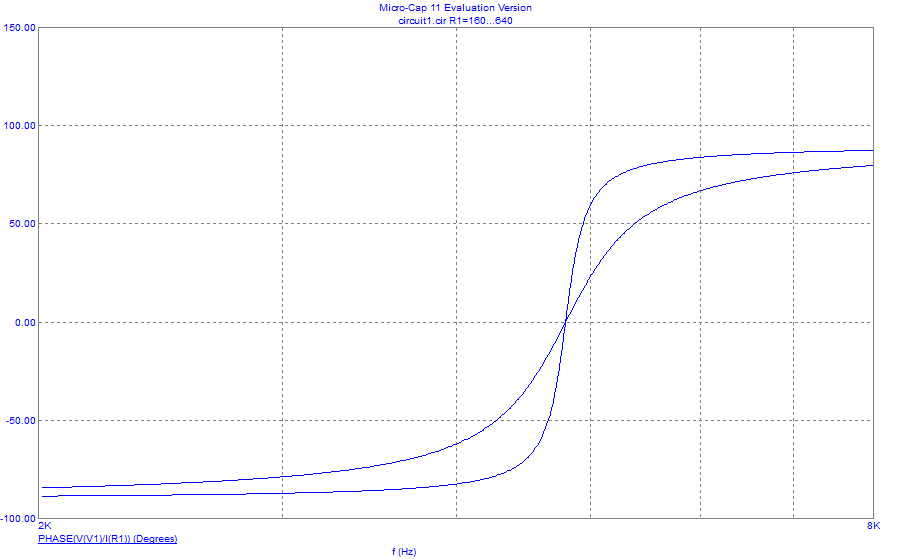
Рисунок 14 – Экспериментальная зависимость фазы входного сопротивления от частоты

при =160 Ом и =640 Ом на одном графике

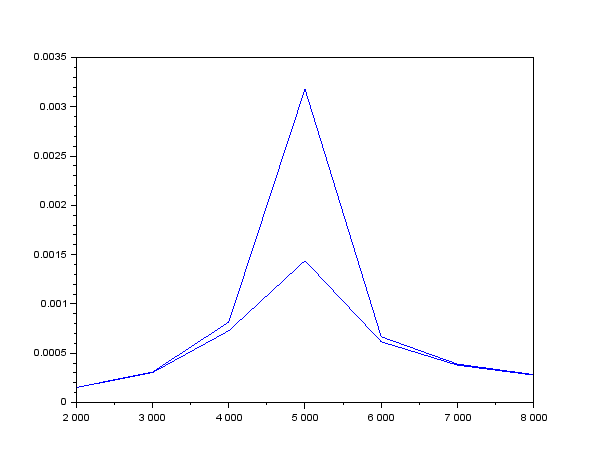
Рисунок 15– Теоретическая зависимость модуля входного тока от частоты

при =160 Ом и =640 Ом на одном графике

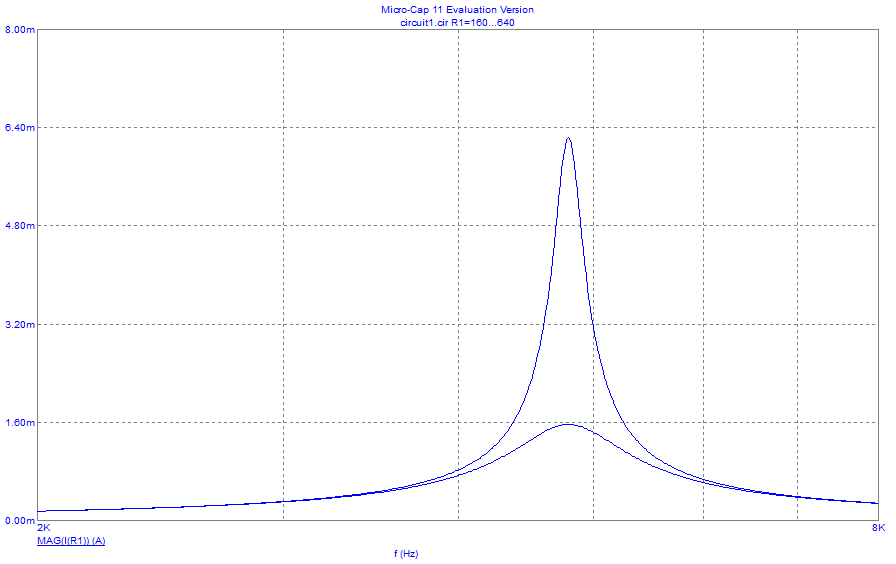
Рисунок 16– Экспериментальная зависимость модуля входного тока от частоты

при =160 Ом и =640 Ом на одном графике

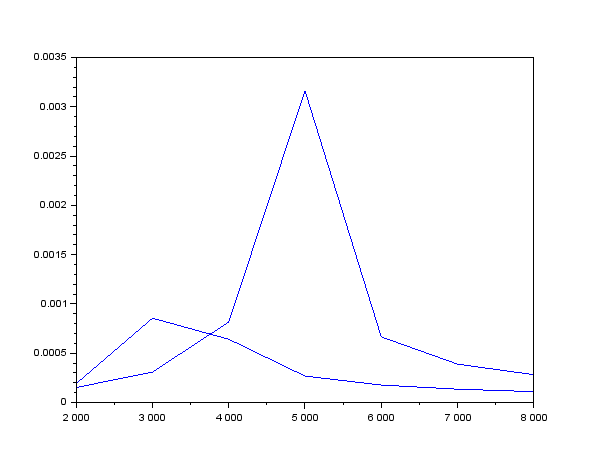
Рисунок 17– Теоретическая зависимость модуля входного тока от частоты

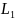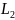при =160 Ом, =0.22 Гн и =0.11 Гн на одном графике

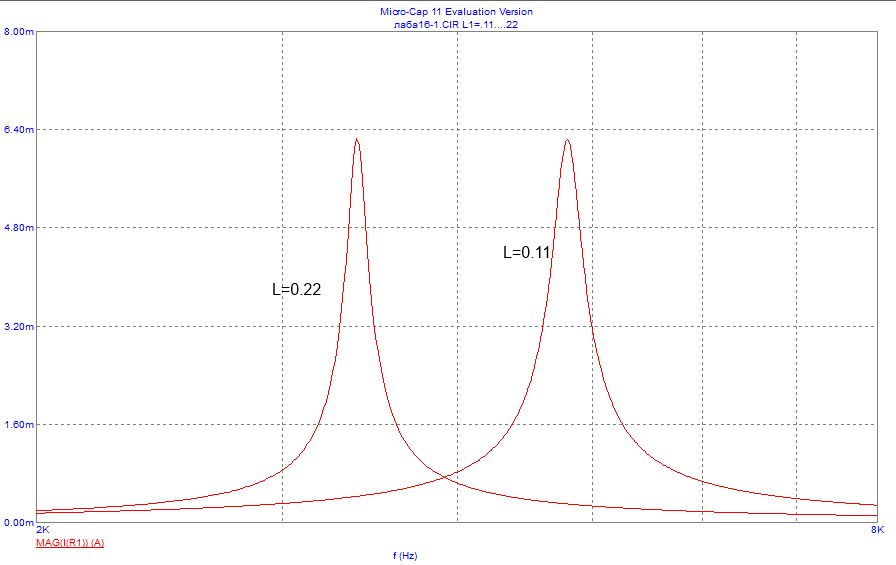
Рисунок 18– Экспериментальная зависимость модуля входного тока от частоты

при =160 Ом, =0.22 Гн и =0.11 Гн на одном графике

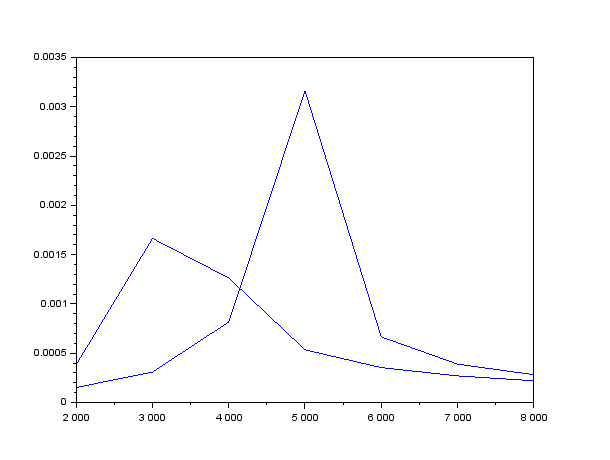
Рисунок 19 – Теоретическая зависимость модуля входного тока от частоты

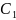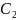при =160 Ом, =10 нФ и =20 нФ на одном графике

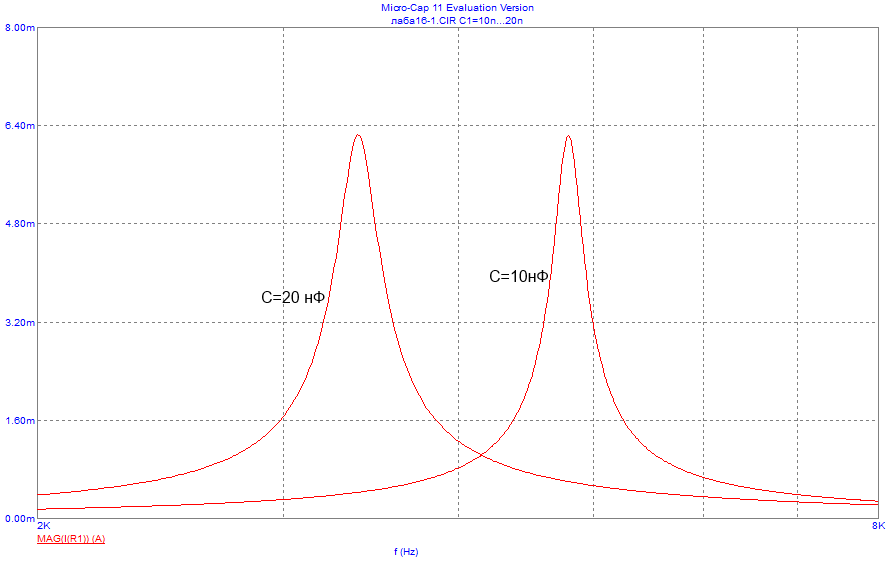
Рисунок 20 – Экспериментальная зависимость модуля входного тока от частоты

при =160 Ом, =10 нФ и =20 нФ на одном графике

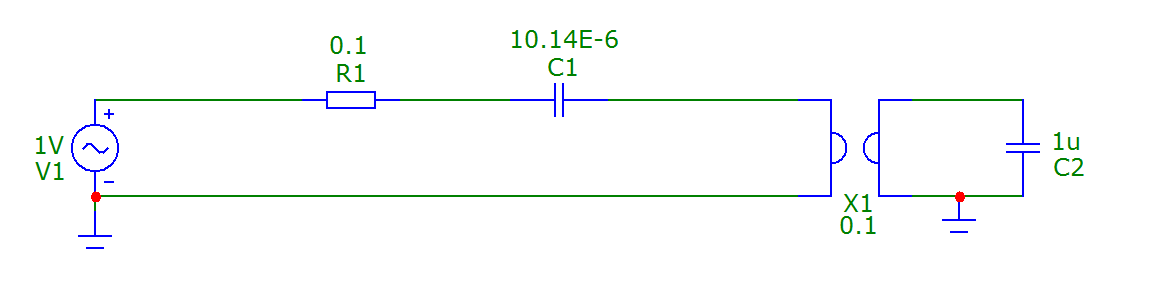
Рисунок 21 – Схема активного колебательного контура с гиратором

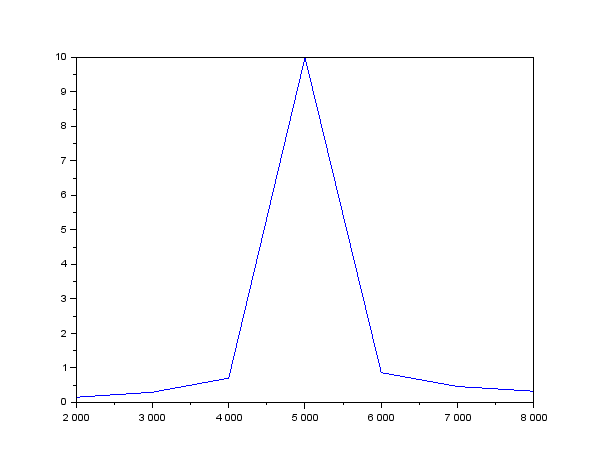
Рисунок 22 – Теоретическая зависимость модуля входного тока от частоты

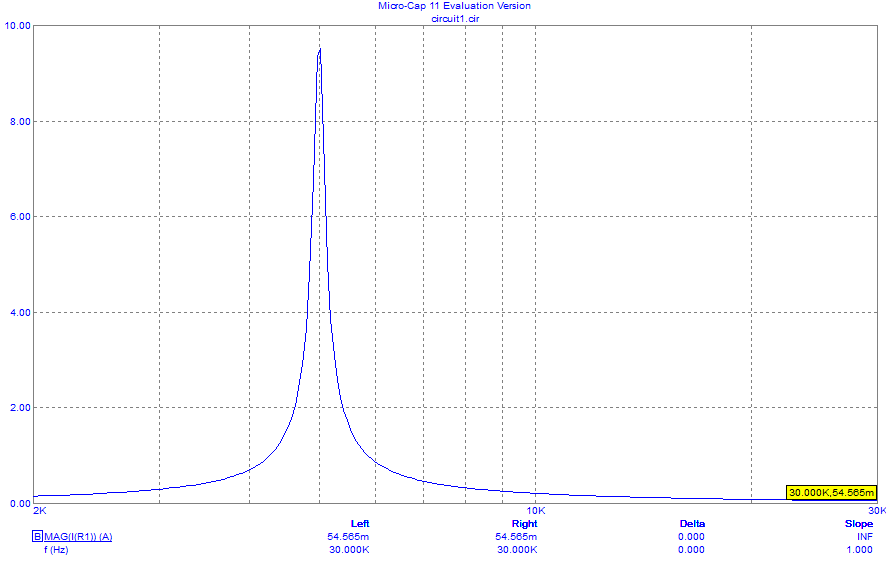
Рисунок 14– Экспериментальная зависимость модуля входного тока от частоты

Контрольные вопросы.

1. Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?

Отношение волнового сопротивления к резистивному  /R = Q, называется добротностью контура, а величина обратная D=1/Q - затуханием. Таким образом, добротность численно равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц, и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений.

2. Как рассчитывается резонансная частота сложного пассивного колебательного контура и как она рассчитывается для схем содержащих гиратор?

3. Что такое добротность последовательного пассивного колебательного контура?

Добротность колебательного контура - величина, определяющая амплитуду и ширину амплитудно частотной характеристики резонанса и говорящая о том, во сколько раз сохраненной энергии в КК больше, чем потери энергии за единичный период колебаний

4. Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

Полоса пропускания (прозрачности) — диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) акустического, радиотехнического, оптического или механического устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.

5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.

Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.

Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, представленного на рис. 2.14, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:

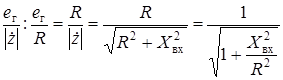= . (3.81)

Реактивная составляющая входного сопротивления контура равна:

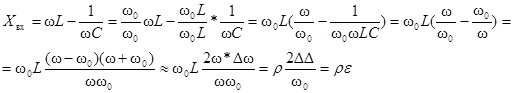 (3.82)

Здесь

 (3.83) - относительная расстройка контура.

Для небольших абсолютных расстроек контура   (в пределах полосы пропускания)

 (3.84)

С учетом этого амплитудно-частотная характеристика контура

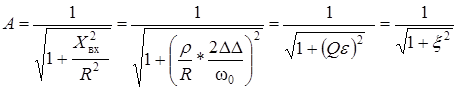, (3.85)

Где: 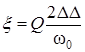  - обобщенная расстройка контура.

Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:

. (3.86)

Фазовая характеристика контура

 (3.87)

При настройке контура в резонанс  , обобщенная расстройка  , реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно  . Характер зависимости  свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности  , который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров  . АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.

Рис.2.15 АЧХ последовательного контура

Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в   раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:

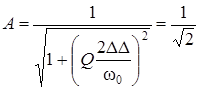. (3.88)

Отсюда полоса пропускания контура на уровне   Будет равна:

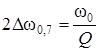 (3.89)

Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:

 (3.90)

Фазовая характеристика последовательного контура, построенная по выражению (2.98), приведена на рис. 3.16.

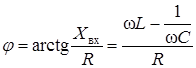 (3.91)