
Лабораторная №3
.docxМинистерство цифрового развития и массовых коммуникаций
Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное
бюджетное образовательное учреждение
высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Отчет по лабораторной работе №2
по дисциплине «Теория вероятностей и математическая статистика»
на тему:
«Описательная статистика»
Выполнила:
Проверила: доцент кафедры
Смирнова Н.И.
Москва 2021

Решение:
i |
ni |
n∙i |
ni - n∙i |
(ni - n∙i)2 |
(ni - n∙i)2/n∙i |
1 |
105 |
99.1979 |
5.8021 |
33.6648 |
0.3394 |
2 |
95 |
100.6029 |
-5.6029 |
31.393 |
0.312 |
3 |
100 |
100.6029 |
-0.6029 |
0.3635 |
0.00361 |
4 |
100 |
100.6029 |
-0.6029 |
0.3635 |
0.00361 |
5 |
102 |
100.6029 |
1.3971 |
1.9518 |
0.0194 |
6 |
98 |
100.6029 |
-2.6029 |
6.7753 |
0.06735 |
7 |
104 |
100.6029 |
3.3971 |
11.54 |
0.1147 |
8 |
96 |
100.6029 |
-4.6029 |
21.1871 |
0.2106 |
9 |
105 |
100.6029 |
4.3971 |
19.3341 |
0.1922 |
10 |
95 |
95.9786 |
-0.9786 |
0.9576 |
0.00998 |
Итого |
1000 |
|
|
|
1.2729 |
Найдем оценки параметров a∙ и b∙ равномерного распределения по формулам:

Найдем плотность предполагаемого равномерного распределения:
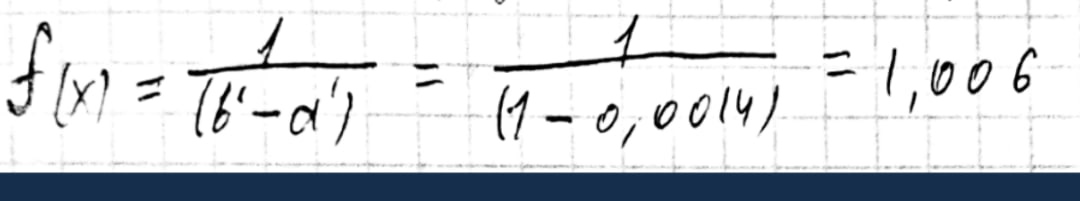
Найдем теоретические частоты:

Остальные ns будут равны:

Находим по таблицам распределения χ2 и заданным значениям s, k и r=2.

Гипотеза Н0 не отвергается. Данные выборки имеют равномерный закон.

Решение:
Критерий согласия Пирсона:
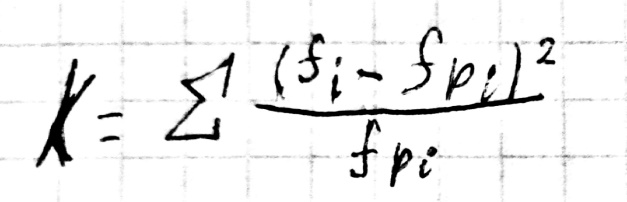
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
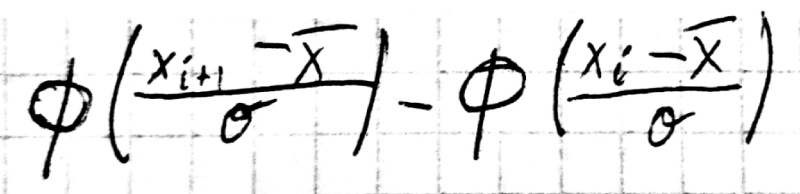
Группы |
Середина интервала, xсер |
Кол-во, fi |
xi·fi |
|x-xср|·fi |
(x-xср)2·fi |
150 - 155 |
152.5 |
6 |
915 |
95.7 |
1526.415 |
155 - 160 |
157.5 |
22 |
3465 |
240.9 |
2637.855 |
160 - 165 |
162.5 |
36 |
5850 |
214.2 |
1274.49 |
165 - 170 |
167.5 |
46 |
7705 |
43.7 |
41.515 |
170 - 175 |
172.5 |
56 |
9660 |
226.8 |
918.54 |
175 - 180 |
177.5 |
24 |
4260 |
217.2 |
1965.66 |
180 - 185 |
182.5 |
8 |
1460 |
112.4 |
1579.22 |
185 - 190 |
187.5 |
2 |
375 |
38.1 |
725.805 |
Итого |
|
200 |
33690 |
1189 |
10669.5 |

xi÷xi+1 |
fi |
x1 = (xi - xср)/s |
x2 = (xi+1 - xср)/s |
Ф(x1) |
Ф(x2) |
pi=Ф(x2)-Ф(x1) |
Ожидаемая частота, 200pi |
Слагаемые статистики Пирсона, Ki |
150 - 155 |
6 |
-2.5197 |
-1.8369 |
-0.4941 |
-0.4671 |
0.027 |
5.4 |
0.06667 |
155 - 160 |
22 |
-1.8369 |
-1.154 |
-0.4671 |
-0.377 |
0.0901 |
18.02 |
0.879 |
160 - 165 |
36 |
-1.154 |
-0.4712 |
-0.377 |
-0.1844 |
0.1926 |
38.52 |
0.1649 |
165 - 170 |
46 |
-0.4712 |
0.2117 |
-0.1844 |
0.0871 |
0.2715 |
54.3 |
1.2687 |
170 - 175 |
56 |
0.2117 |
0.8945 |
0.0871 |
0.3159 |
0.2288 |
45.76 |
2.2915 |
175 - 180 |
24 |
0.8945 |
1.5774 |
0.3159 |
0.4429 |
0.127 |
25.4 |
0.07717 |
180 - 185 |
8 |
1.5774 |
2.2602 |
0.4429 |
0.4887 |
0.0458 |
9.16 |
0.1469 |
185 - 190 |
2 |
2.2602 |
2.9431 |
0.4887 |
0.4985 |
0.0098 |
1.96 |
0.000816 |
|
200 |
|
|
|
|
|
|
4.8956 |
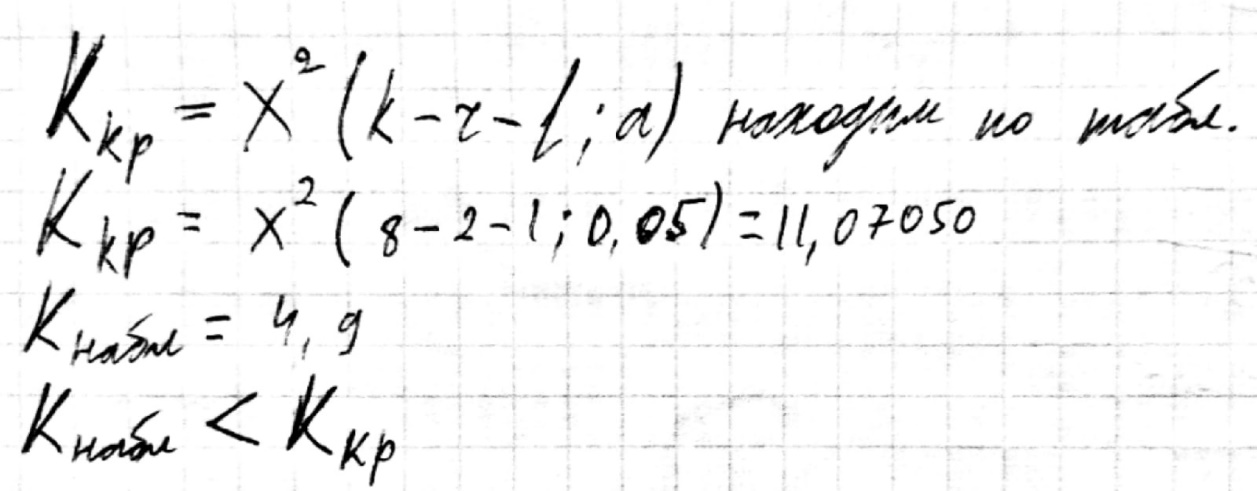
Гипотеза Н0 не отвергается. Данные выборки имеют нормальное распределение.

xi |
Кол-во, ni |
xi·ni |
Накопленная частота, S |
|x-xср|·ni |
(x-xср)2·ni |
Относительная частота, ni/n |
0 |
8 |
0 |
8 |
15.867 |
31.469 |
0.133 |
1 |
17 |
17 |
25 |
16.717 |
16.438 |
0.283 |
2 |
16 |
32 |
41 |
0.267 |
0.00444 |
0.267 |
3 |
10 |
30 |
51 |
10.167 |
10.336 |
0.167 |
4 |
6 |
24 |
57 |
12.1 |
24.402 |
0.1 |
5 |
2 |
10 |
59 |
6.033 |
18.201 |
0.0333 |
6 |
1 |
6 |
60 |
4.017 |
16.134 |
0.0167 |
Итого |
60 |
119 |
|
65.167 |
116.983 |
1 |

xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
ni |
8 |
17 |
16 |
10 |
6 |
2 |
1 |
pi |
8/60=0.133 |
17/60=0.283 |
16/60=0.267 |
10/60=0.167 |
6/60=0.1 |
2/60=0.033 |
1/60=0.017 |
|
0,133 |
0,416 |
0,683 |
0,85 |
0,95 |
0,9833 |
1 |
|
0,0778 |
0,242 |
0,504 |
0,7673 |
0,9251 |
0,9846 |
0,998 |
|
0,0552 |
0,174 |
0,179 |
0,0827 |
0,0249 |
0,0013 |
0,002 |
Проверяем гипотезу, что с.в. Х имеет нормальное распределение, т.е.
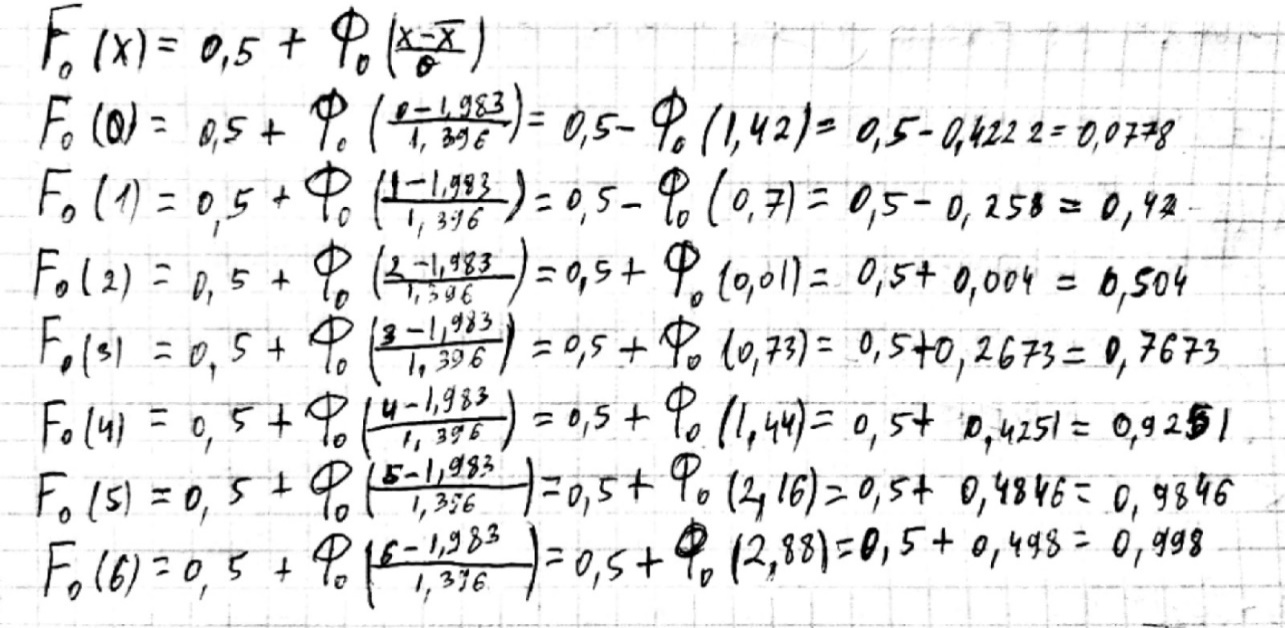
Максимальное отклонение эмпирической функции распределения от теоретической:
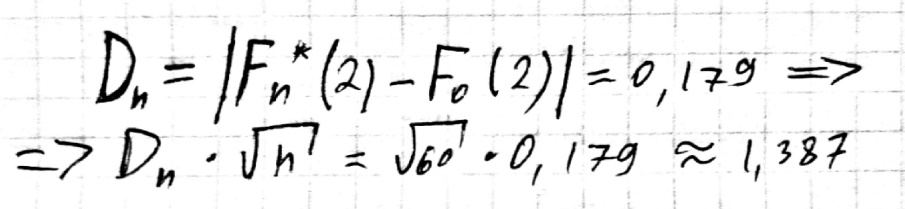
Критическое значение критерия Колмогорова равно
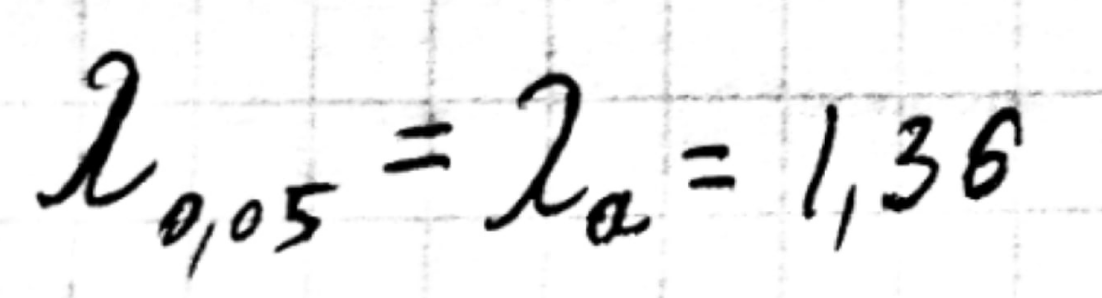
Т.к.
 ,
то гипотеза о нормальном распределении
не отвергается.
,
то гипотеза о нормальном распределении
не отвергается.



