
- •Алгоритм для построения выпуклой оболочки набора точек (Jarvis)
- •Цель работы.
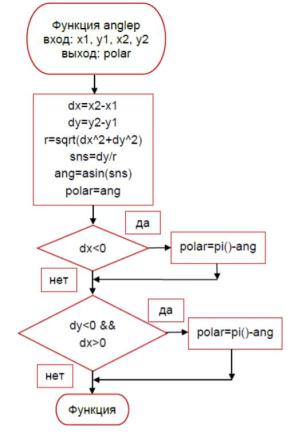
- •Блок-схема программы для нахождения полярного угла вектора 1-2.
- •Текст программы 1.
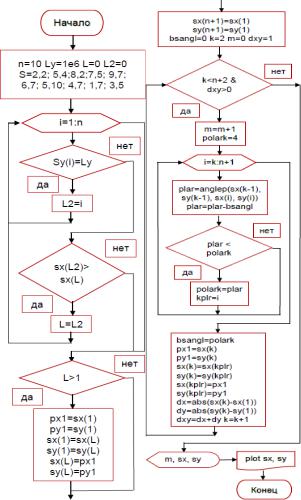
- •Блок-схема алгоритма построения выпуклой оболочки набора точек (Jarvis) и вывода результатов
- •Текст программы 2 (Алгоритм Джарвиса).
- •Листинг 2
- •Вывод:
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра физической электроники и технологии
ОТЧЕТ по лабораторной работе №6
по дисциплине «Информационные технологии» Тема: Алгоритмы и программы решения задач комбинаторики
Студентка гр. 0207 |
|
Лиоско Е.П. |
|
Преподаватель |
|
|
Рябцев И.А. |
Санкт-Петербург
2021
Алгоритм для построения выпуклой оболочки набора точек (Jarvis)
Цель работы.
Изучение и программирование алгоритма построения выпуклой оболочки набора точек.
Блок-схема программы для нахождения полярного угла вектора 1-2.
Текст программы 1.
clear;
clc;
sx=[1, -1, -1, 1, 1]; sy=[1, 1, -1, -1, 1]; for i=1:4
x1=sx(i); y1=sy (i); x2=sx(i+1); y2=sy(i+1);
p=anglePolar(x1,y1,x2,y2);
disp(p);
end
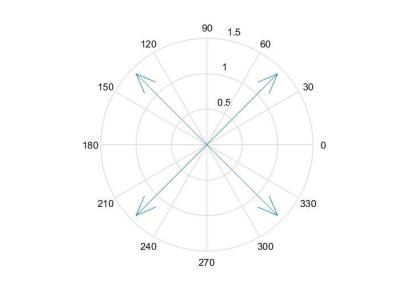
hp=compass(sx,sy); % построение векторов
2
function[polar]=angle(x1,y1,x2,y2) dx=x2-x1;
dy=y2-y1; r=sqrt(dx^2+dy^2); sns=dy/r; ang=asin(sns); polar=ang;
if dx<0 polar=pi()-ang;
else
if (dy<0) && (dx>0) polar=pi()-ang;
end
end end
Листинг 1
3.1416 -1.5708
0
1.5708
Блок-схема алгоритма построения выпуклой оболочки набора точек (Jarvis) и вывода результатов
3
Текст программы 2 (Алгоритм Джарвиса).
clc; |
|
|
|
|
|
|
|
clear all; |
|
|
|
|
|
||
n = |
10; |
|
|
|
|
|
|
l = |
1; |
|
|
|
|
|
|
l2 = 1; |
|
|
|
|
|
|
|
s = |
[2, |
2; 5, 4; 8, 2; |
|
||||
7, |
5; |
9, |
7; |
6, |
7; |
|
|
5, |
10; |
4, |
7; |
1, |
7; |
3, |
5]; |
sx = [2 |
5 8 7 9 6 5 4 1 3 0]; |
||||||
sy = [2 |
4 2 5 7 7 10 7 7 5 0]; |
||||||
for |
i = |
2:n |
|
|
|
|
|
if |
sy(i) <= sy(l) |
|
|
||||
l2 |
= i; |
|
|
|
|
|
|
end |
|
|
|
|
|
|
|
if |
sx(l2) < sx(l) |
|
|
||||
l = l2; end
end
4
if l > 1
px = sx(1); py = sy(1);
sx(1) = sx(l); sy(1) = sy(l); sx(l) = px; sx(l) = py; end
sx(n+1) = sx(1); sy(n+1) = sy(1); bsangl = 0;
k = 2; m = 0;
dxy = 1;
while (k < (n+2) && dxy > 0) m = m+1;
polark = 100; for i = k:(n+1)
polar = anglePolar(sx(k-1), sy(k-1), sx(i), sy(i)); if polar < polark && polar >= bsangl
polark = polar; kplr = i;
end end
bsangl = polark; px = sx(k);
py = sy(k);
sx(k) = sx(kplr); sy(k) = sy(kplr); sx(kplr) = px; sy(kplr) = py;
dx = abs(sx(k)-sx(1)); dy = abs(sy(k)-sy(1)); dxy = dx+dy;
k = k + 1; end
plot(sx, sy, 'bo'); hold on;
plot(sx(1:m+1), sy(1:m+1), 'b-'); disp(m);
disp(sx);
disp(sy);
function polar = anglePolar(x1, y1, x2, y2) dx = x2-x1;
dy = y2-y1;
r = sqrt(dx.^2+dy.^2); sns = dy/r;
5
