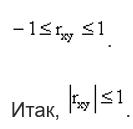25. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева.

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Закон больших чисел важен, поскольку он гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Важно помнить, что закон применим только тогда, когда рассматривается большое количество испытаний.

26. Усиленный закон больших чисел, теорема Бернулли. Теорема Пуассона.

Усиленный закон больших чисел утверждает, что при определённых условиях с вероятностью единица происходит неограниченное сближение средних арифметических последовательности случайных величин с некоторыми постоянными величинами.

27. Центральная предельная теорема.

28. Многомерные случайные величины. Функция распределения и плотность распределения.

Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин обозначать . Такая система называется также многомерной случайной величиной.

Функцией распределения вероятностей системы двух случайных величин называется функция двух аргументов , равная вероятности совместного выполнения двух неравенств и , т. е.

Сформулируем основные свойства функции распределения вероятностей системы двух случайных величин.

Свойство 1.

или символически

Свойство 2.

или

Свойство 3.

или

Свойство 4. Функция распределения является неубывающей функцией по каждому аргументу:

Предположим, что функция распределения непрерывна и дважды дифференцируема. Тогда смешанная частная производная функции

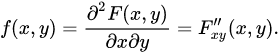
Функция называется плотностью распределения системы непрерывных случайных величин . Зная плотность распределения , можно определить вероятность попадания случайной точки в произвольную область

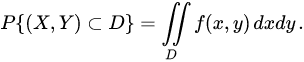
Выразим функцию распределения системы через плотность распределения :

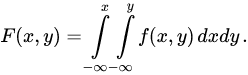
Рассмотрим свойства плотности распределения системы двух случайных величин.

Свойство 1. Плотность распределения есть функция неотрицательная: .

Свойство 2. Двойной несобственный интеграл с бесконечными пределами от плотности распределения системы равен единице:

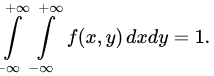
29. Двумерное дискретное распределение.

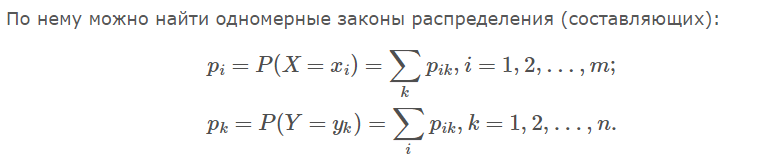
30. Независимость случайных величин. Условные распределения случайных величин.

31. Числовые характеристики в условных законах распределения.

32. Корреляционный момент, коэффициент корреляции. Их свойства.

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий, составляющих пользуются и другими характеристиками, к числу которых относятся корреляционный момент и коэффициент корреляции.

Корреляционным моментом K_xy (или ковариацией, или моментом связи) двух случайных величин X и Y называется математическое ожидание произведения отклонений этих величин.

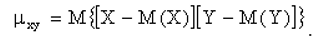
Для вычисления корреляционного момента дискретных величин используют формулу

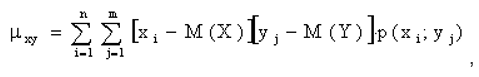
а для непрерывных величин – формулу

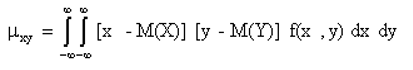
Корреляционный момент служит для характеристики связи между величинами X и Y. Корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.

Корреляционный момент можно записать в виде

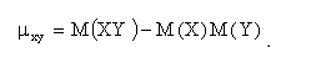
ТЕОРЕМА Корреляционный момент двух независимых случайных величин X и Y равен нулю.

Доказательство. Так как X и Y – независимые случайные величины, то их отклонения X – M(X) и Y – M(Y) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим

.

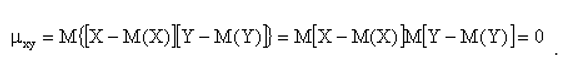
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины.

Пусть, например, X и Y были измерены в сантиметрах и ; если измерить X и Y в миллиметрах, то и . Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того, чтобы устранить этот недостаток, вводят новую числовую характеристику – коэффициент корреляции.

Коэффициентом корреляции r_xy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:

.

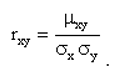
Так как размерность равна произведению размерностей величин X и Y, имеет размерность величины X, имеет размерность величины Y, то — безразмерная величина. Таким образом, r_xy величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.

Очевидно, коэффициент корреляции независимых случайных величин равен нулю, так как .

ТЕОРЕМА Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:

.

Доказательство. Введем в рассмотрение случайную величину и найдем ее дисперсию . Выполнив выкладки, получим

.

Любая дисперсия неотрицательна, поэтому .

Отсюда

Введя случайную величину , аналогично найдем

Объединим:

,

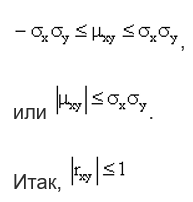
ТЕОРЕМА Абсолютная величина коэффициента корреляции не превышает единицы:

.

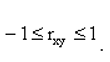
Доказательство. Разделим обе части двойного неравенства на произведение положительных чисел :