17. Геометрическое распределение.
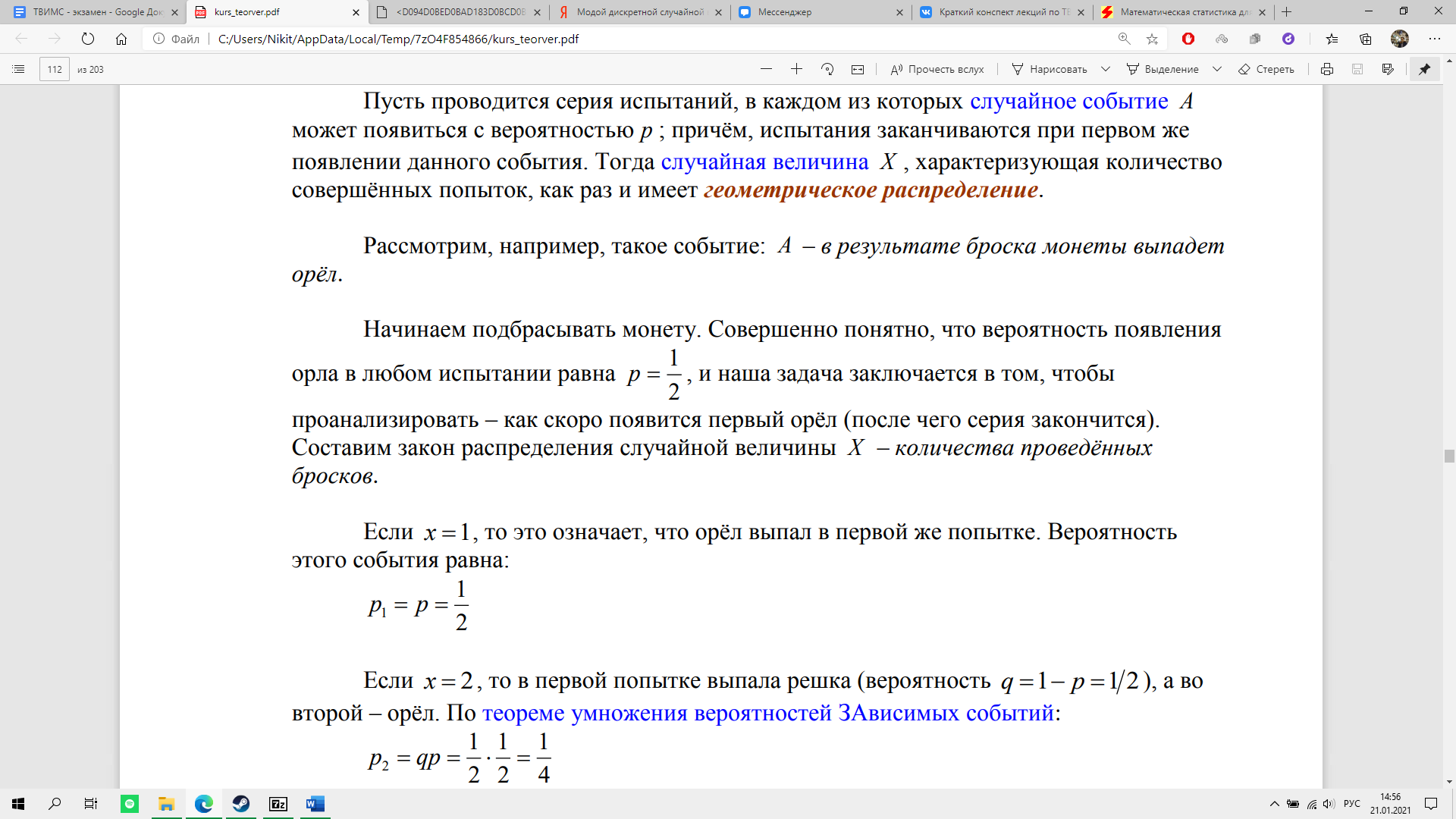
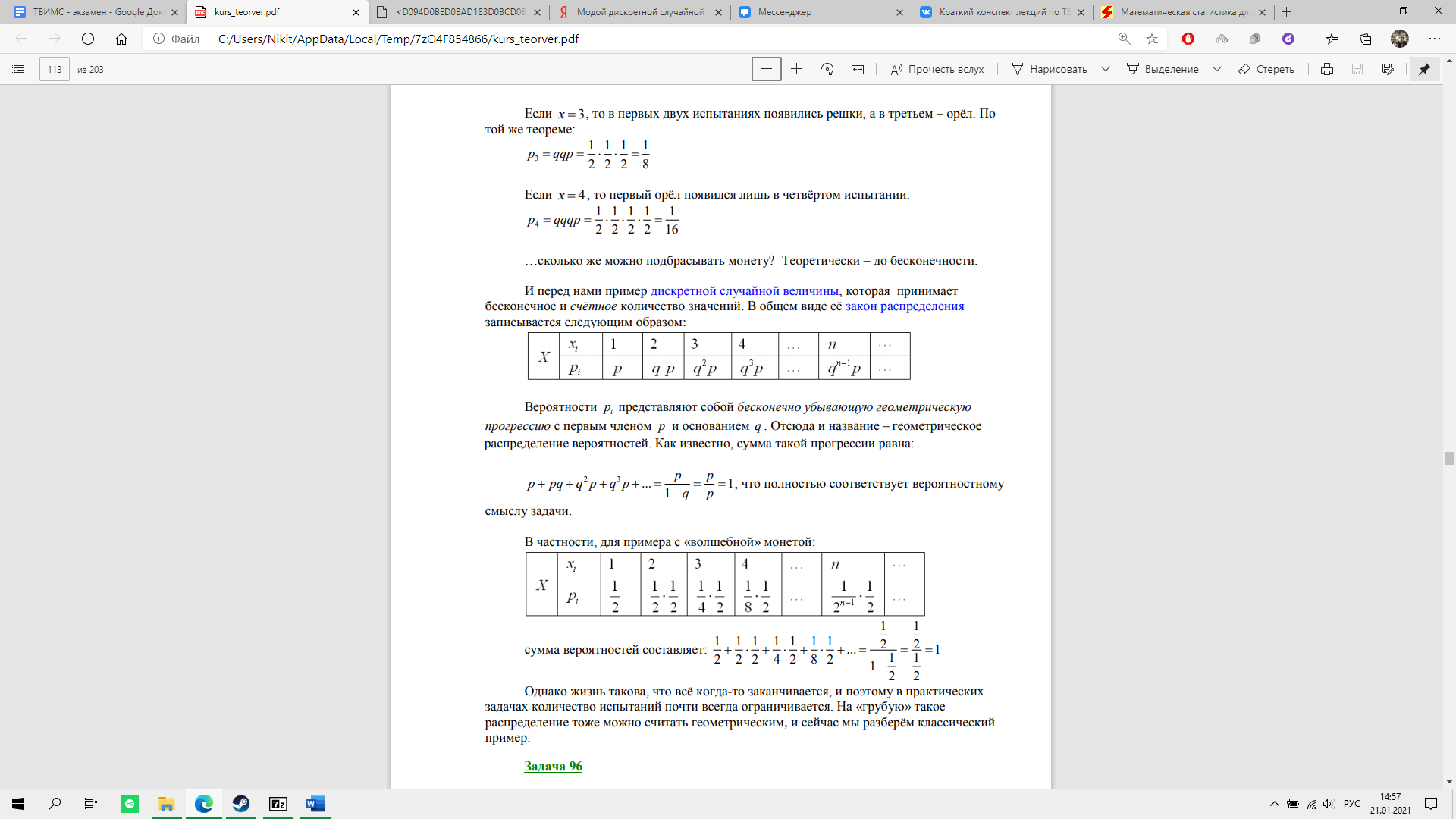
Пусть проводится серия испытаний, в каждом из которых случайное событие А может появиться с вероятностью р; причём, испытания заканчиваются при первом же появлении данного события. Тогда случайная величина Х, характеризующая количество совершённых попыток, как раз и имеет геометрическое распределение.
18. Непрерывные случайные величины. Плотность распределения. Функция распределения.
В отличие от дискретной случайной величины, НСВ может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы (т.к. действительных чисел несчётно много). В этой связи непрерывную случайную величину задают функциями двух типов:
Функцией распределения F(x);
Функцией плотности распределения f(x).
Как отмечалось ранее, функция распределения F(x) непрерывной случайной величины X определяется точно так же, как и в дискретном случае, повторим определение:
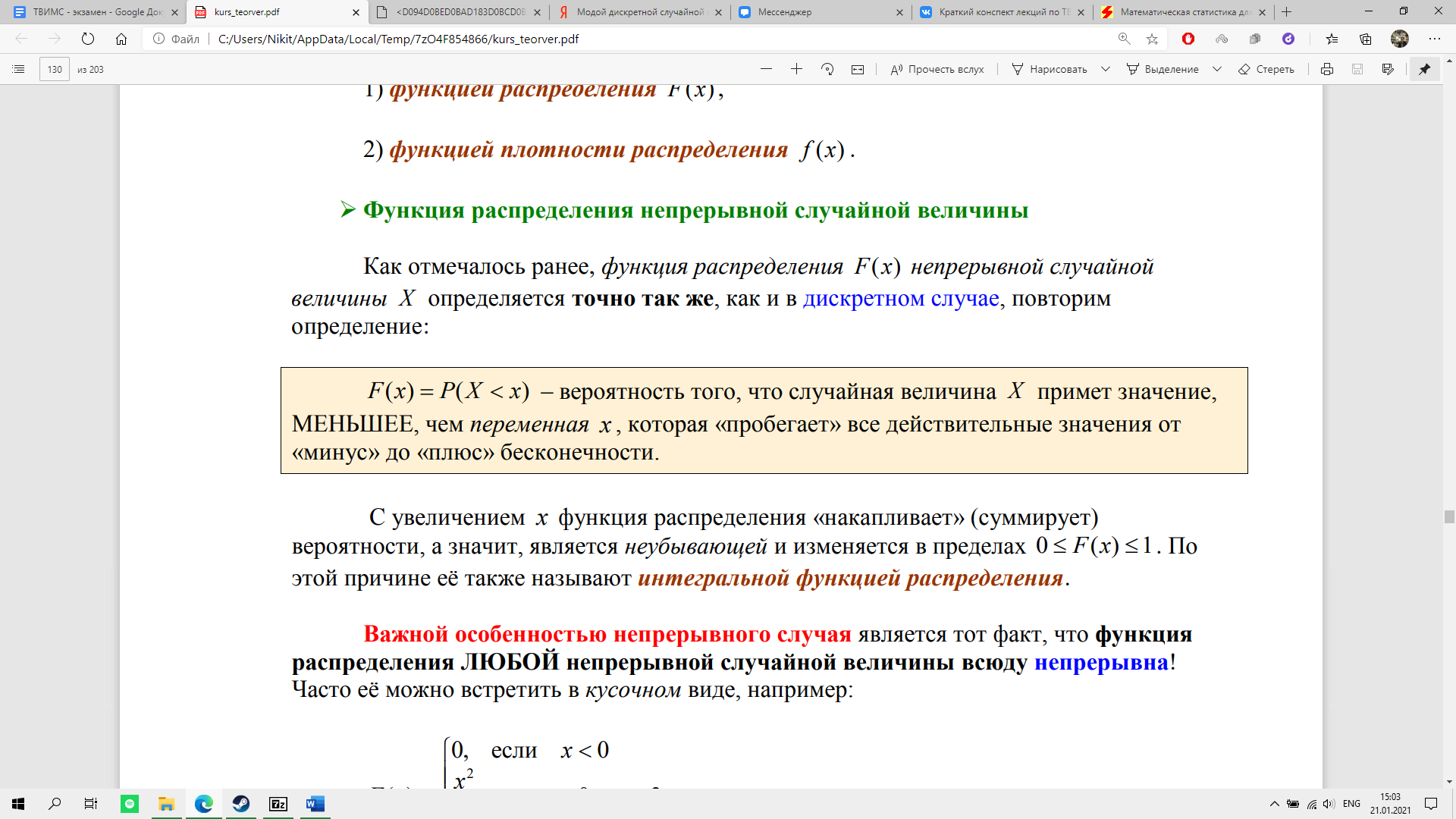
С увеличением x функция распределения
«накапливает» (суммирует) вероятности,
а значит, является неубывающей и
изменяется в пределах:
.
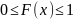По этой причине её также называют
интегральной функцией распределения.
Важной особенностью непрерывного случая является тот факт, что функция распределения ЛЮБОЙ непрерывной случайной величины всюду непрерывна.
Функция плотности распределения вероятностей или дифференциальная функция распределения. Она представляет собой производную функции распределения F’(x) = f(x).
Примечание: для дискретной случайной величины такой функции не существует
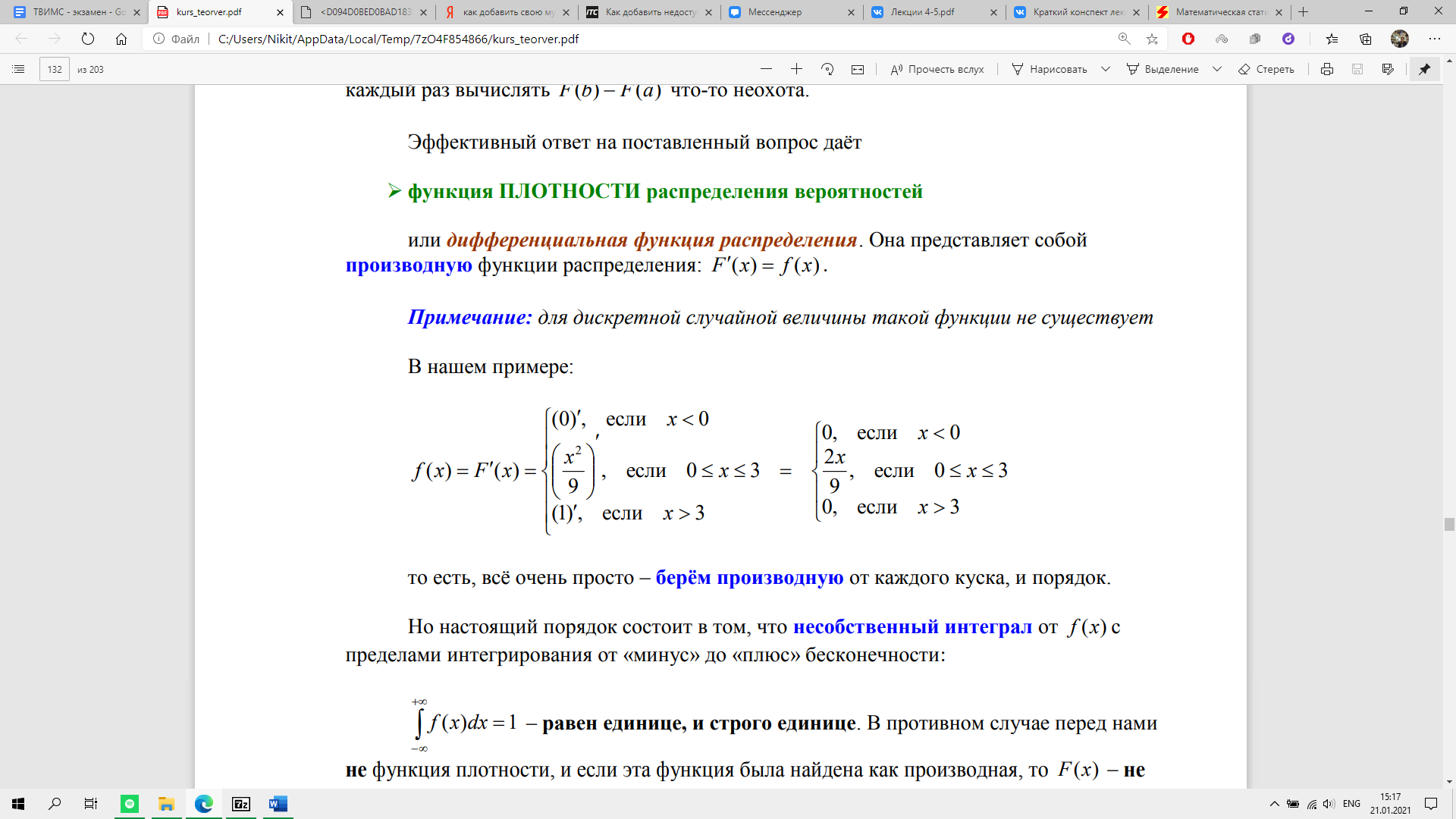
То есть, всё очень просто – берём производную от каждого куска, и порядок.
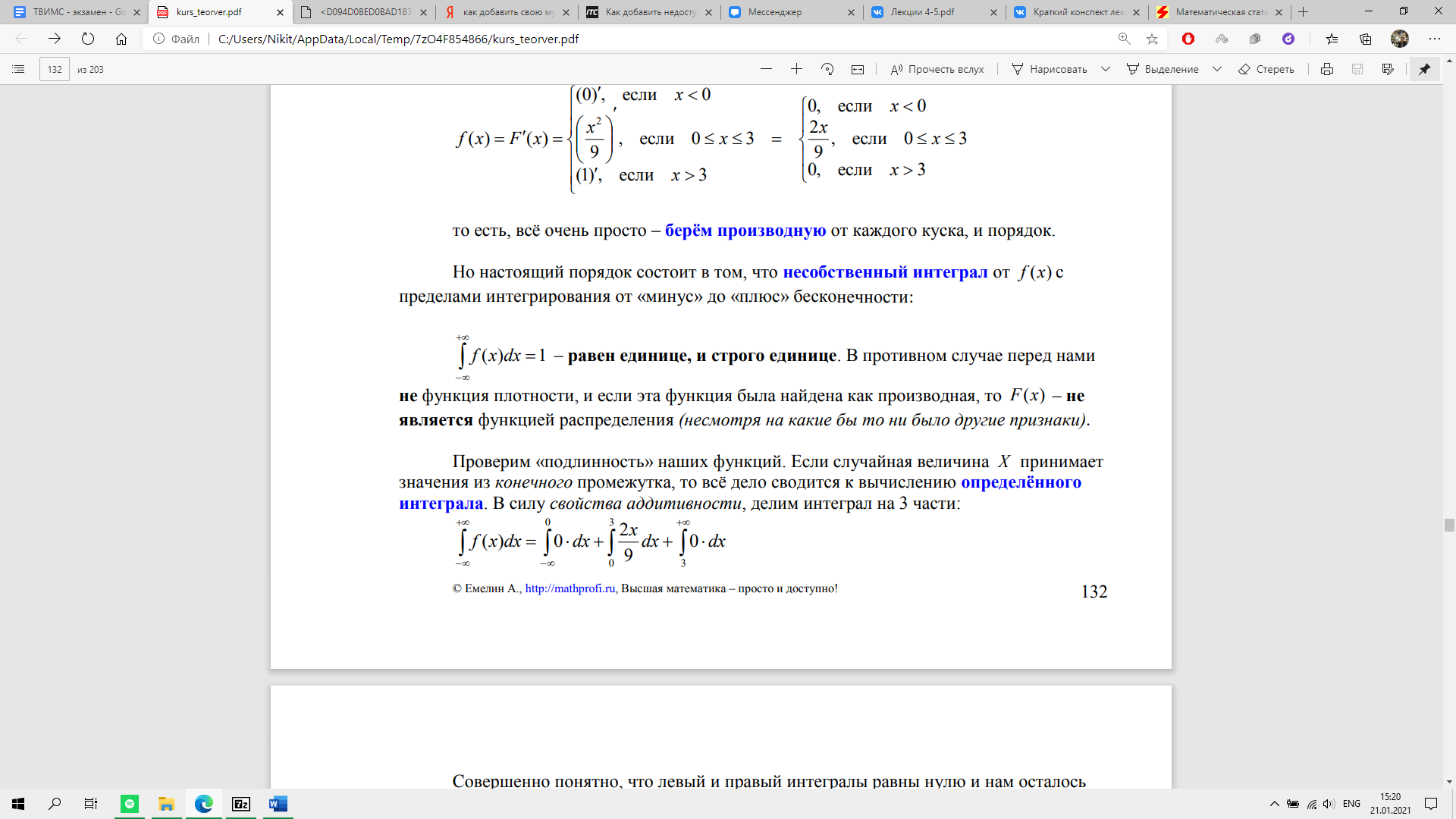
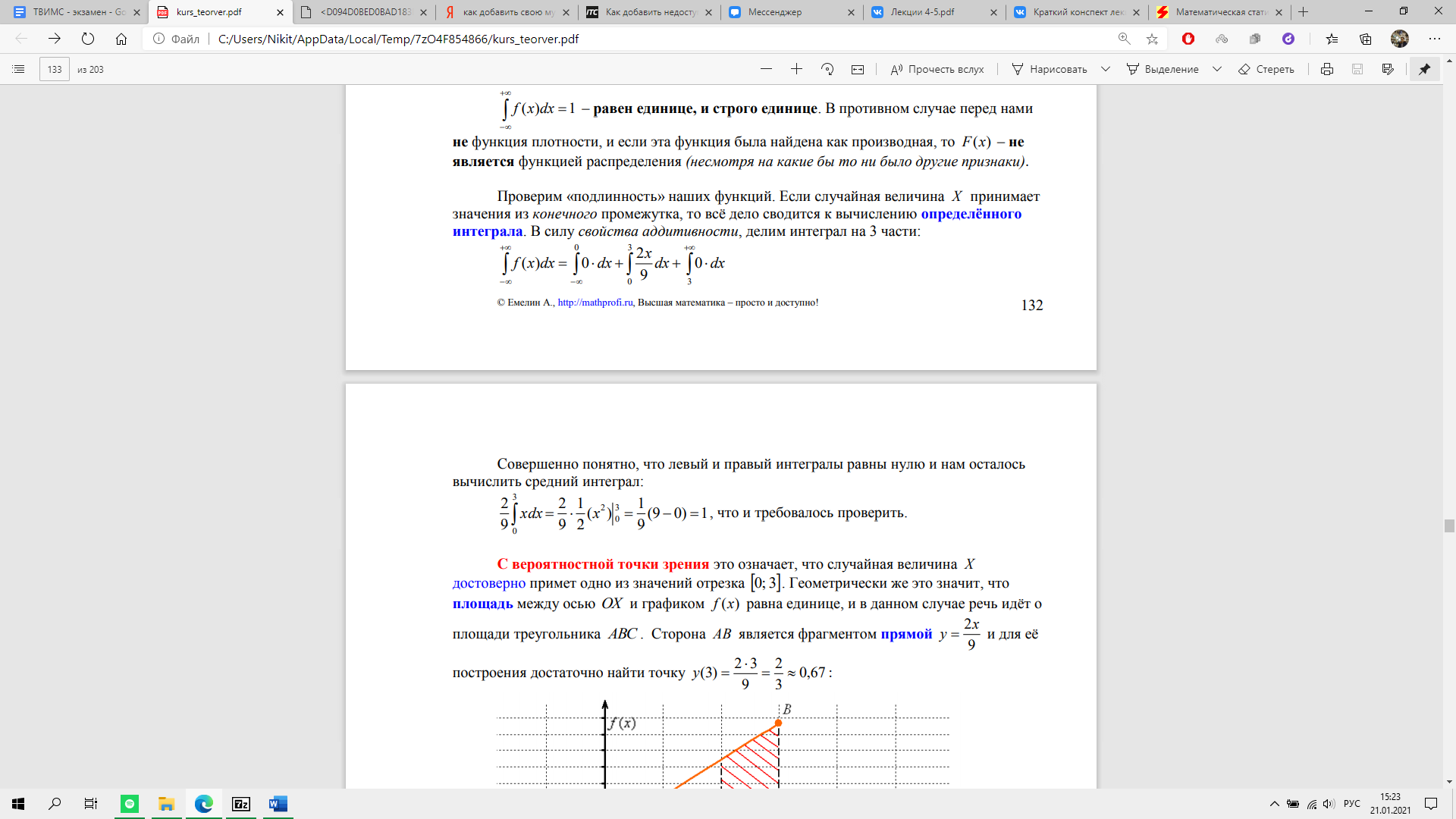
Пример:
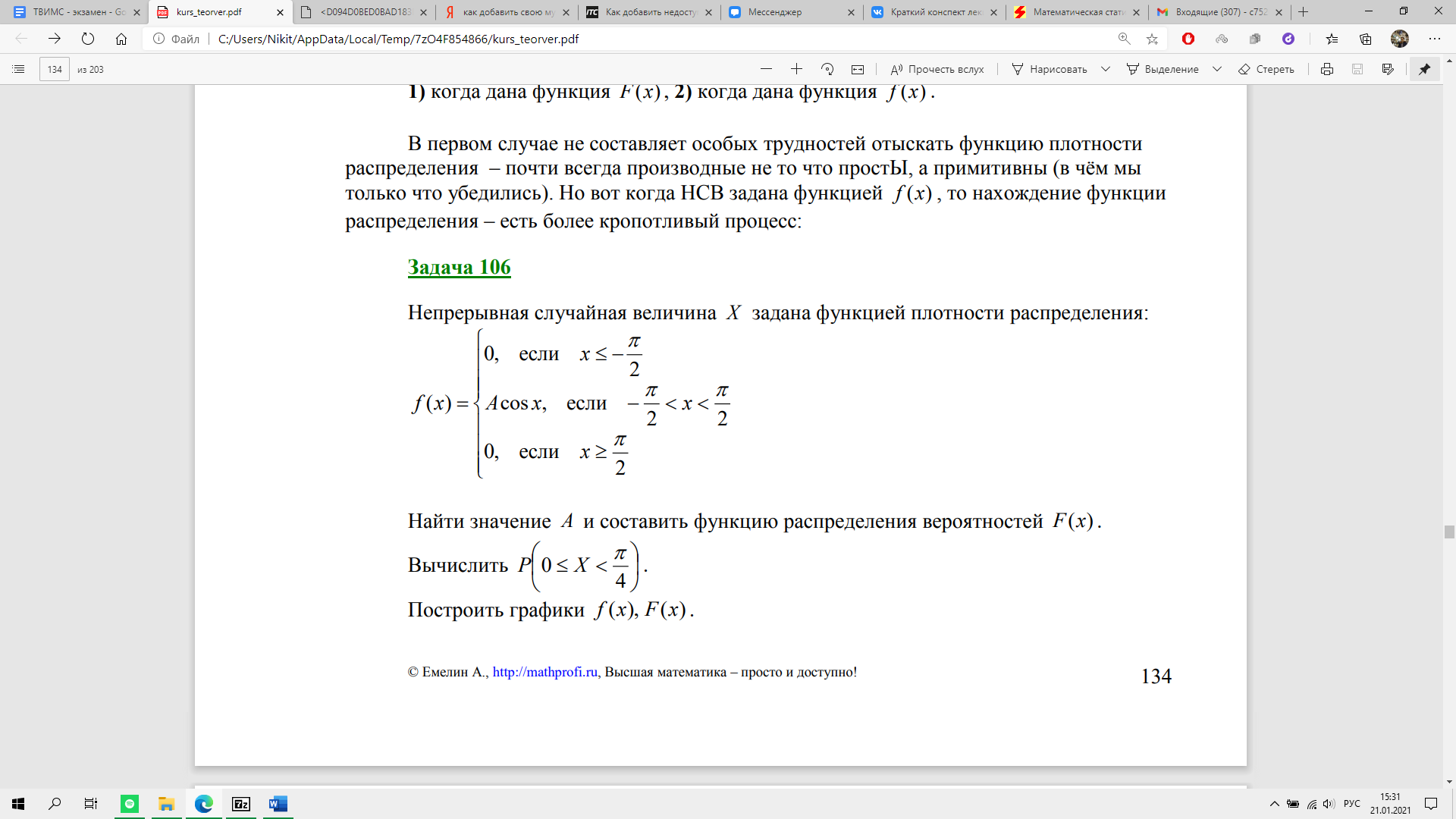
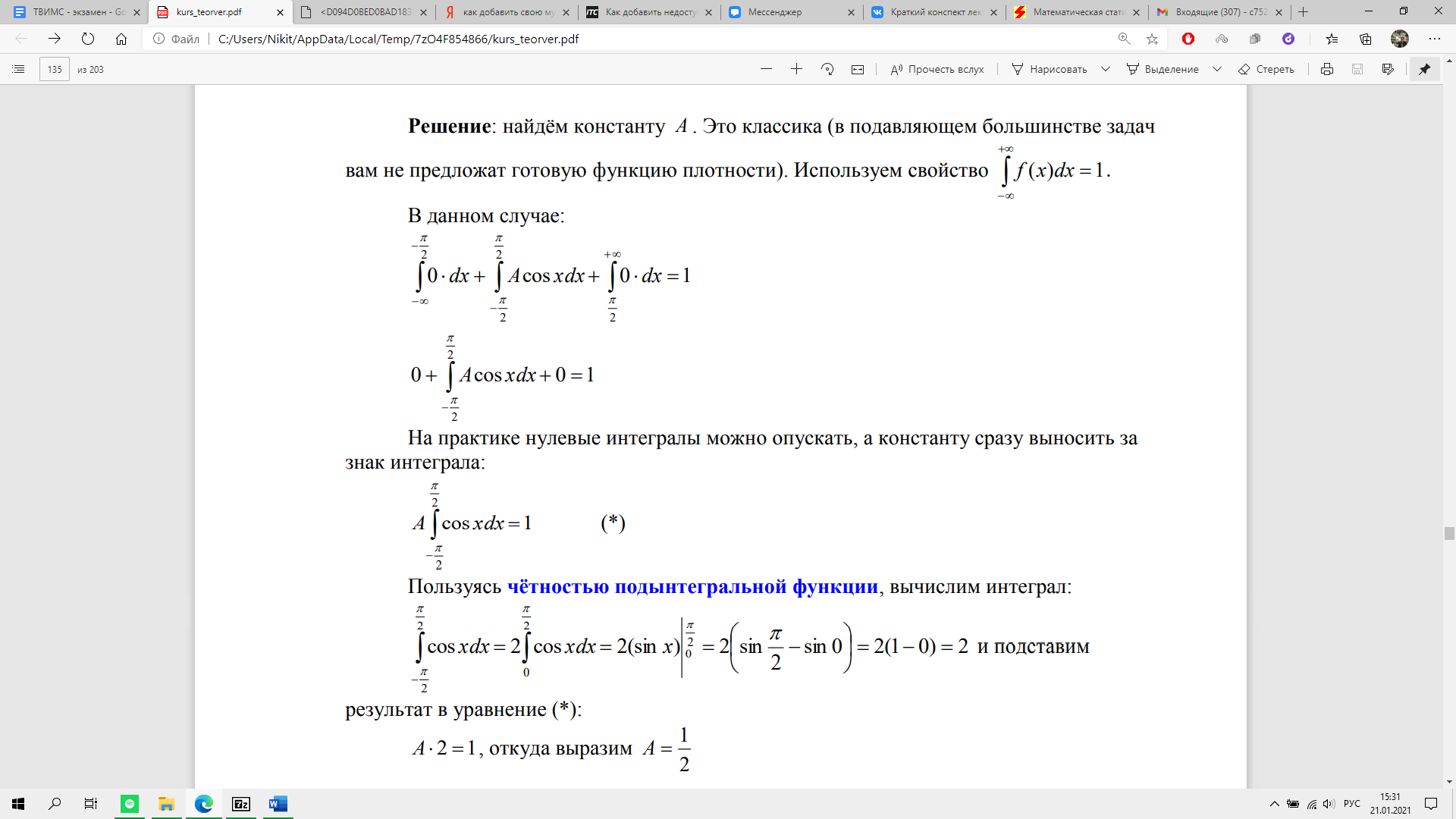
19. Числовые характеристики непрерывной случайной величины. Математическое ожидание
Дискретная случайная величина полностью характеризуется своим законом распределения, заданным в виде таблицы или с помощью функции распределения. Однако, в некоторых случаях закон распределения полностью не известен и приходится довольствоваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают некоторые свойства случайной величины. Такие числа будем называть числовыми характеристиками случайной величины.
Одной из таких характеристик является математическое ожидание.
Математическим ожиданием дискретной случайной величины X называют сумму произведений всех ее возможных значений на их вероятности. По определению, математическое ожидание случайной величины есть величина неслучайная, т.е. постоянная.
Вероятностный смысл математического ожидания - математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины, т.е. оно характеризует среднее значение случайной величины.
Дисперсия
Дисперсией (рассеянием) случайной величины - называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: .
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
https://3dstroyproekt.ru/teorija-verojatnosti/chislovye-harakteristiki-nepreryvnoj-sluchajnoj-velichiny
20. Коэффициент асимметрии. Эксцесс.
Вычисление
асимметрии и эксцесса позволяет
установить симметричность распределения
случайной величины
относительно
Для этого находят третий центральный
момент, характеризующий асимметрию
закона распределения случайной величины.
Если он равен нулю
,
то случайная величина
симметрично распределена относительно
математического ожидания
Поскольку
имеет размерность случайной величины
в кубе, то вводят безразмерную величину
— коэффициент асимметрии:
Центральный
момент четвертого порядка используется
для определения эксцесса, характеризует
плосковершиннисть или гостровершиннисть
плотности вероятности
Эксцесс вычисляется по формуле
Число 3 вычитается для сравнения отклонения от центрального закона распределения (нормального закона), для которого подтверждается равенство:
Итак,
для нормального закона распределения.
Если эксцесс положительный
то на графике функция распределения
остро вершину и для отрицательных
значений
более пологую. Таким образом можно
установить отклонения заданного закона
от нормального. Для наглядности при
различных значениях асимметрии и
эксцесса
графики плотности вероятностей
изображены на рисунках ниже
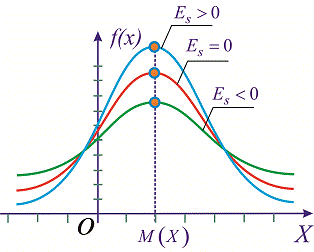
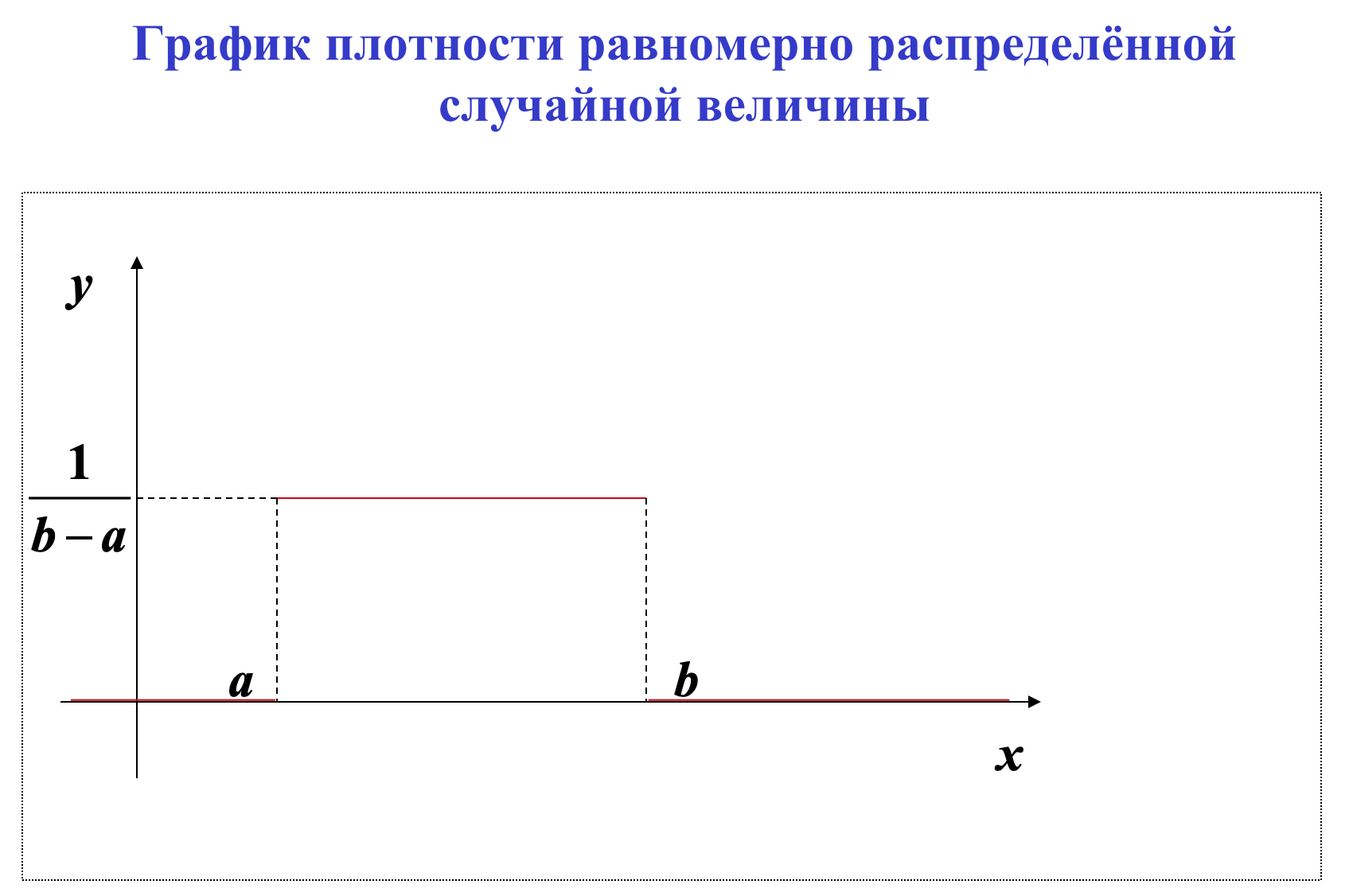
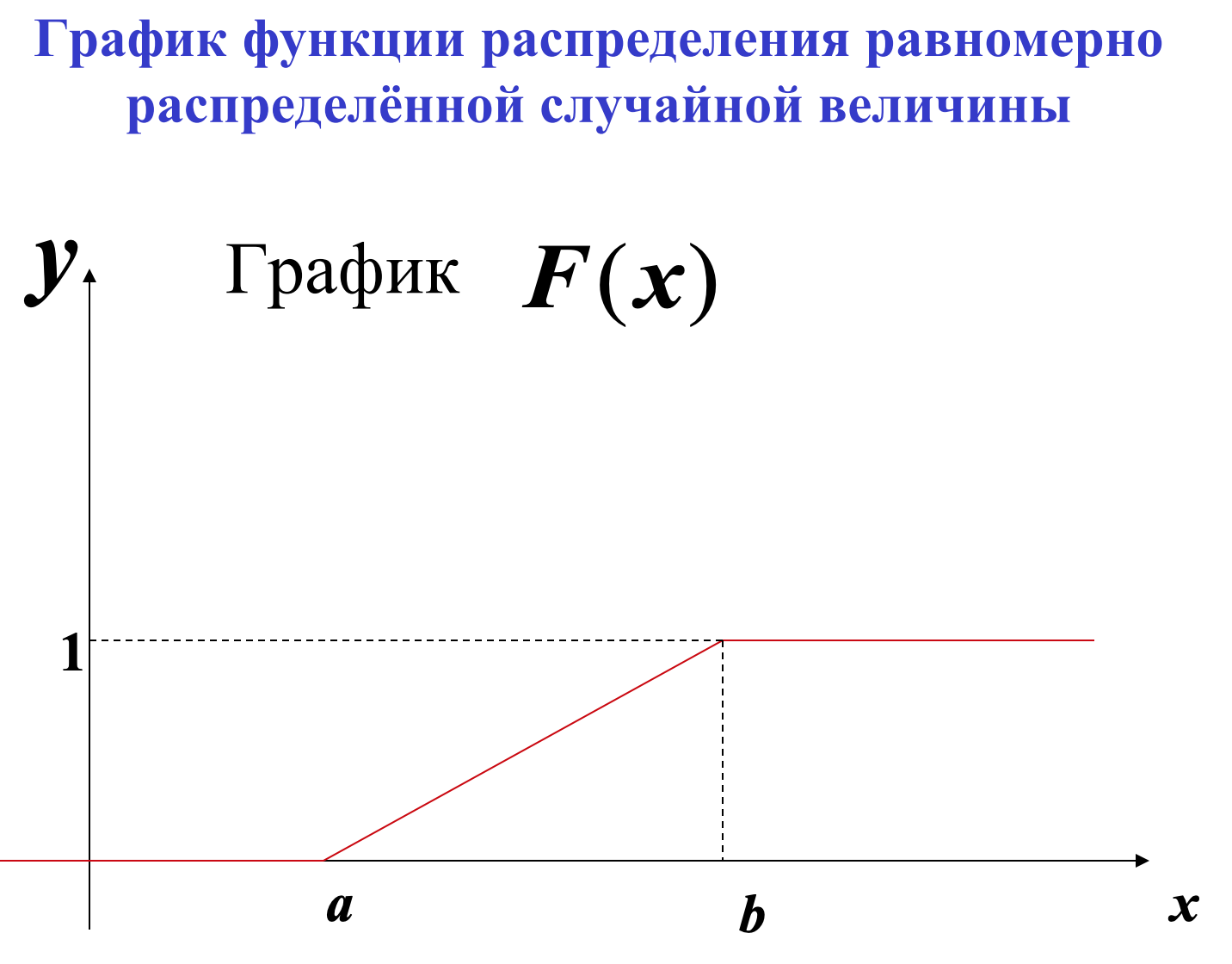
21. Равномерное распределение.
Равномерное распределение вероятностей (mathprofi.ru)
22. Показательное распределение.
Показательное распределение вероятностей (mathprofi.ru)
23. Нормальное распределение.
Нормальное распределение вероятностей (mathprofi.ru)
24. Правило трех сигм.
Нормальное распределение вероятностей (mathprofi.ru)
Суть правила
Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
Вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения равно 0,9973
На практике: если распределение случайной величины неизвестно, но условие, указанное в данном правиле выполняется, то есть основание предполагать, что случайная величина распределена нормально.
Таким образом, значениями случайной величины, которые отклоняются от математического ожидания больше, чем на часто пренебрегают, как маловероятными
