13. Дисперсия и ее свойства. Среднеквадратическое отклонение. Дисперсия

Дисперсией (рассеянием) случайной величины - называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: .

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю:

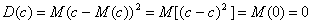
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:

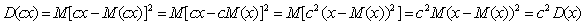
3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:

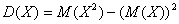
4. Дисперсия алгебраической суммы и разности конечного числа независимых случайных величин равна сумме их дисперсий:

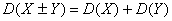
5. Дисперсия суммы случайной величины и константы равна дисперсии этой случайной величины (т.е. дисперсия не зависит от сдвига значений случайной величины): 𝐷(𝐶 + 𝑋) = 𝐷(𝑋).

Среднеквадратическое отклонение

Средним квадратичным отклонением случайной величины называется корень квадратный из дисперсии

.

Среднее квадратичное отклонение случайной величины, как и дисперсия, характеризует меру рассеяния значений случайной величины около ее математического ожидания.

Пример дисперсии

Вероятность изготовления бракованной детали на первом станке составляет 3%, на втором станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей. Найти математическое ожидание и дисперсию числа бракованных деталей.

Математическое ожидание биномиального распределения: Дисперсия:

Математическое ожидание величины – числа бракованных деталей на 1-м станке: Дисперсия:

Математическое ожидание величины – числа бракованных деталей на 2-м станке: Дисперсия:

Математическое ожидание числа бракованных деталей:

Дисперсия числа бракованных деталей:

Ответ: ;

14. Мода. Медиана, начальные и центральные моменты. Мода

Модой дискретной случайной величины 𝑋 называют ее значение, которое принимается с наибольшей вероятностью по сравнению с двумя соседними значениями. Обозначают моду случайной величины 𝑋: 𝑀О𝑋, или строчной 𝑚О𝑋 и: max 𝑖 𝑃(𝑋 = 𝑥𝑖) = 𝑃(𝑋 = 𝑀О).

Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки:

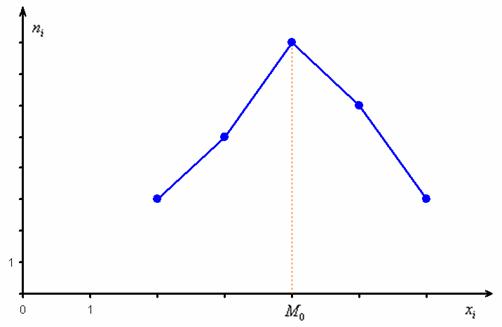
Распределения могут быть унимодальными (имеющими одну моду), бимодальными (две моды), мультимодальными (имеющими несколько мод). Если же в распределении посередине не максимум, а минимум, то такое распределение называется антимодальным.

Чаще всего мода случайной величины встречается в результате проведения серии эксперимента, описываемого случайной величиной, например, используется в экономических расчетах, при выявлении наибольшего спроса на какой-либо товар и т.д.

Медиана

Медианой дискретной случайной величины 𝑋 (обозначают 𝑀е𝑋) называют такое ее значение, для которого справедливо равенство: 𝑃(𝑋 < 𝑀𝑒 ) = 𝑃(𝑋 > 𝑀𝑒), т.е., вероятность того, что случайная величина окажется меньше или больше медианы равна 0,5. Графически, медианой является абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам. Заметим, что так как вся площадь должна быть равна единице, то функция распределения в этой точке: 𝐹(𝑀𝑒 )=0,5. Если даны первичные данные, то сортируем их по возрастанию либо убыванию и находим середину ранжированного ряда.