10. Функция распределения вероятностей и ее свойства. Функция распределения вероятностей

Функцией распределения случайной величины называют функцию, значение которой в точке x равно вероятности того, что значение случайной величины строго меньше x.

По определению, 𝐹𝑋(𝑥) = 𝑃(𝑋 < 𝑥). Для дискретной случайной величины график функции распределения является ступенчатой функцией со скачками 𝑝𝑖 в точках 𝑥𝑖 и представляет собой набор отрезков, параллельных оси OX, напоминает «лесенку», т.е. функция распределения – сумма вероятностей тех значений, которые расположены левее 𝑥:

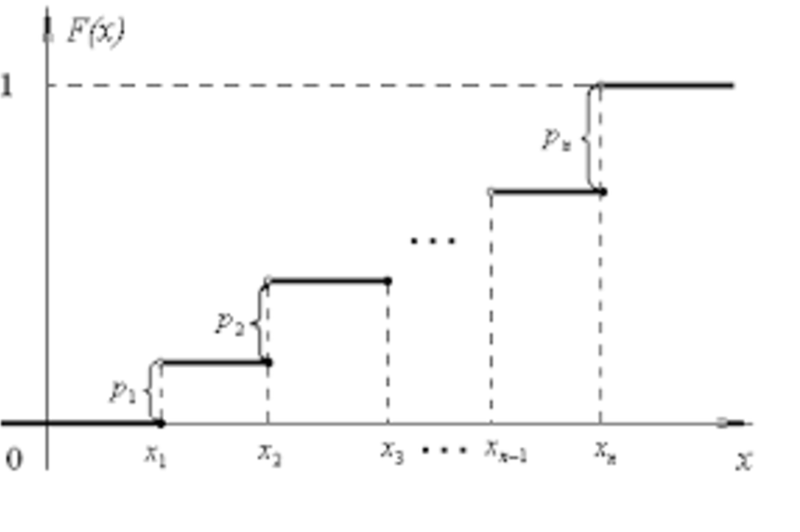
Свойства функции

1. Функция распределения от минус бесконечности равна 0:

𝐹(−∞) = lim 𝑥→−∞ 𝐹𝑋(𝑥) = lim 𝑥→−∞ 𝑃(𝑋 < 𝑥) = 𝑃(𝑋 < −∞) = 0.

2. Функция распределения от плюс бесконечности равна 1:

𝐹(+∞) = lim 𝑥→+∞ 𝐹𝑋(𝑥) = 1.

3. Функция 𝐹𝑋(𝑥) неубывающая.

4. 𝑃(𝑋 ≥ 𝑥) = 1 − 𝑃(𝑋 < 𝑥) = 1 − 𝐹𝑋(𝑥).

5. Вероятность попадания случайной величины в интервал [х1, x2] равна приращению её функции распределения на этом интервале

𝑃(𝑥1 ≤ 𝑋 ≤ 𝑥2) = 𝐹(𝑥2) − 𝐹(𝑥1).

6. 𝐹𝑋(𝑥) непрерывна слева, т.е. lim 𝑥→𝑥0−0 𝐹𝑋 (𝑥) = 𝐹𝑋(𝑥0).

11. Плотность распределения вероятностей и ее свойства.

Плотность распределения вероятностей непрерывной случайной величины Х есть функция f(x) – первая производная от функции распределения F(x).

Плотность распределения вероятностей может быть представлена графиком кривой.

Эта кривая обладает следующими свойствами:

а) лежит не ниже горизонтальной оси,

б) площадь между кривой и горизонтальной осью равна единице.

Вероятности события соответствует площадь под кривой (выше горизонтальной оси) между точками

12. Математическое ожидание и его свойства. Математическое ожидание

Дискретная случайная величина полностью характеризуется своим законом распределения, заданным в виде таблицы или с помощью функции распределения. Однако, в некоторых случаях закон распределения полностью неизвестен и приходится довольствоваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают некоторые свойства случайной величины. Такие числа будем называть числовыми характеристиками случайной величины.

Одной из таких характеристик является математическое ожидание.

Математическим ожиданием дискретной случайной величины X называют сумму произведений всех ее возможных значений на их вероятности. Обозначают его M(X), иногда 𝑚𝑋.

𝑀(𝑋) = 𝑥1𝑝1 + 𝑥2𝑝2 + ⋯ + 𝑥𝑛𝑝𝑛 = .

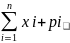По определению, математическое ожидание случайной величины есть величина неслучайная, т.е. постоянная.

Вероятностный смысл математического ожидания - математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины, т.е. оно характеризует среднее значение случайной величины.

Пример. найти математическое ожидание случайной величины X, равной числу выпавших очков при бросании симметричной игральной кости.

Решение. Запишем закон распределения случайной величины:

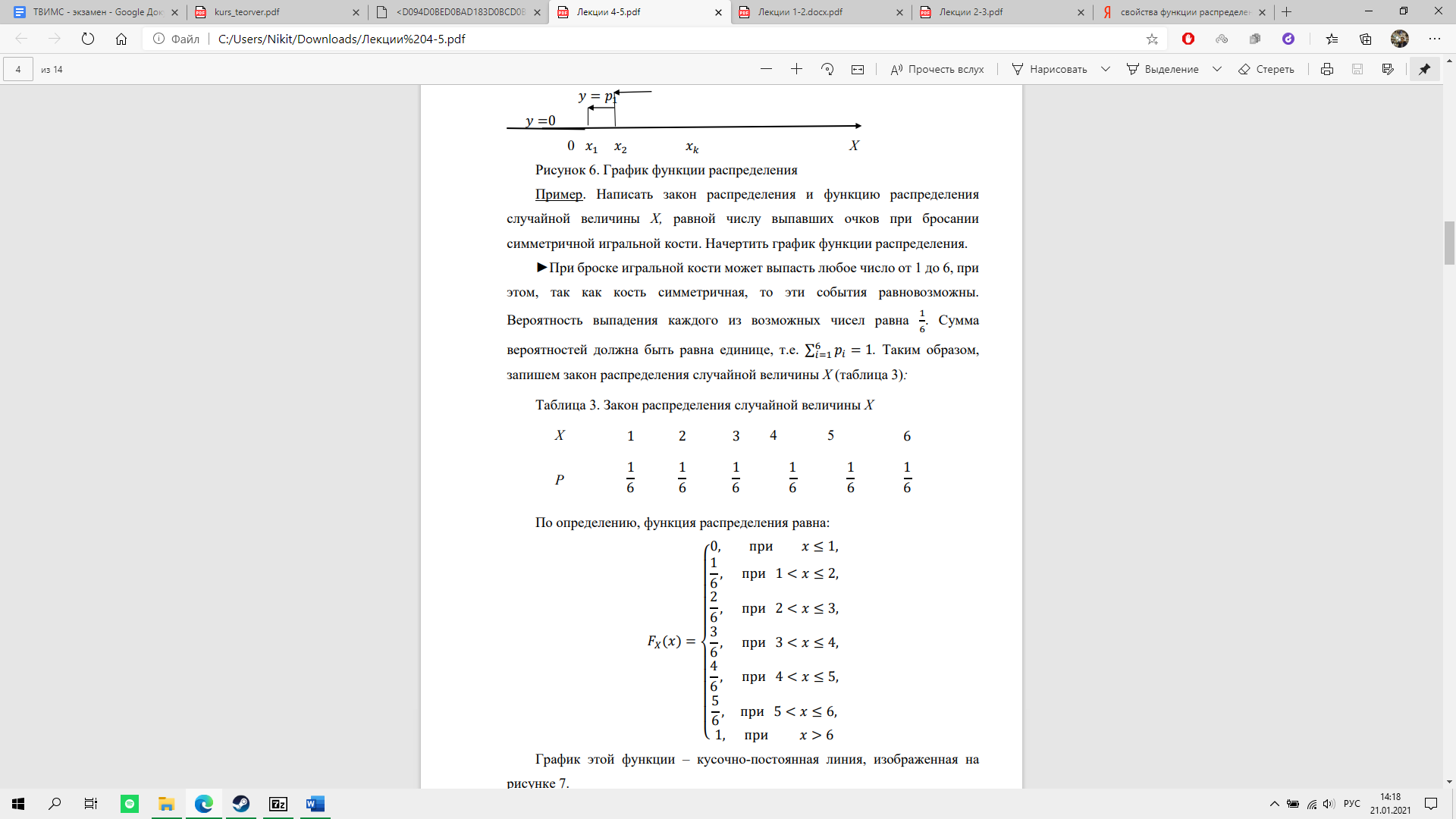
По формуле мат. ожидания имеем:

𝑀(𝑋) = 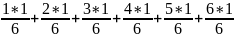= = 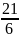3,5.

Свойства математического ожидания

1. Математическое ожидание постоянной величины равно этой самой постоянной:

𝑀(𝐶) = 𝐶.

2. Постоянный множитель можно выносить за знак математического ожидания:

𝑀(𝐶𝑋) = 𝐶 ∙ 𝑀(𝑋).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

𝑀(𝑋𝑌) = 𝑀(𝑋) ∙ 𝑀(𝑌).

4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

𝑀(𝑋 + 𝑌) = 𝑀(𝑋) + 𝑀(𝑌).