8. Интегральная теорема Лапласа. Отклонение относительной частоты от постоянной вероятности. Интегральная теорема Лапласа

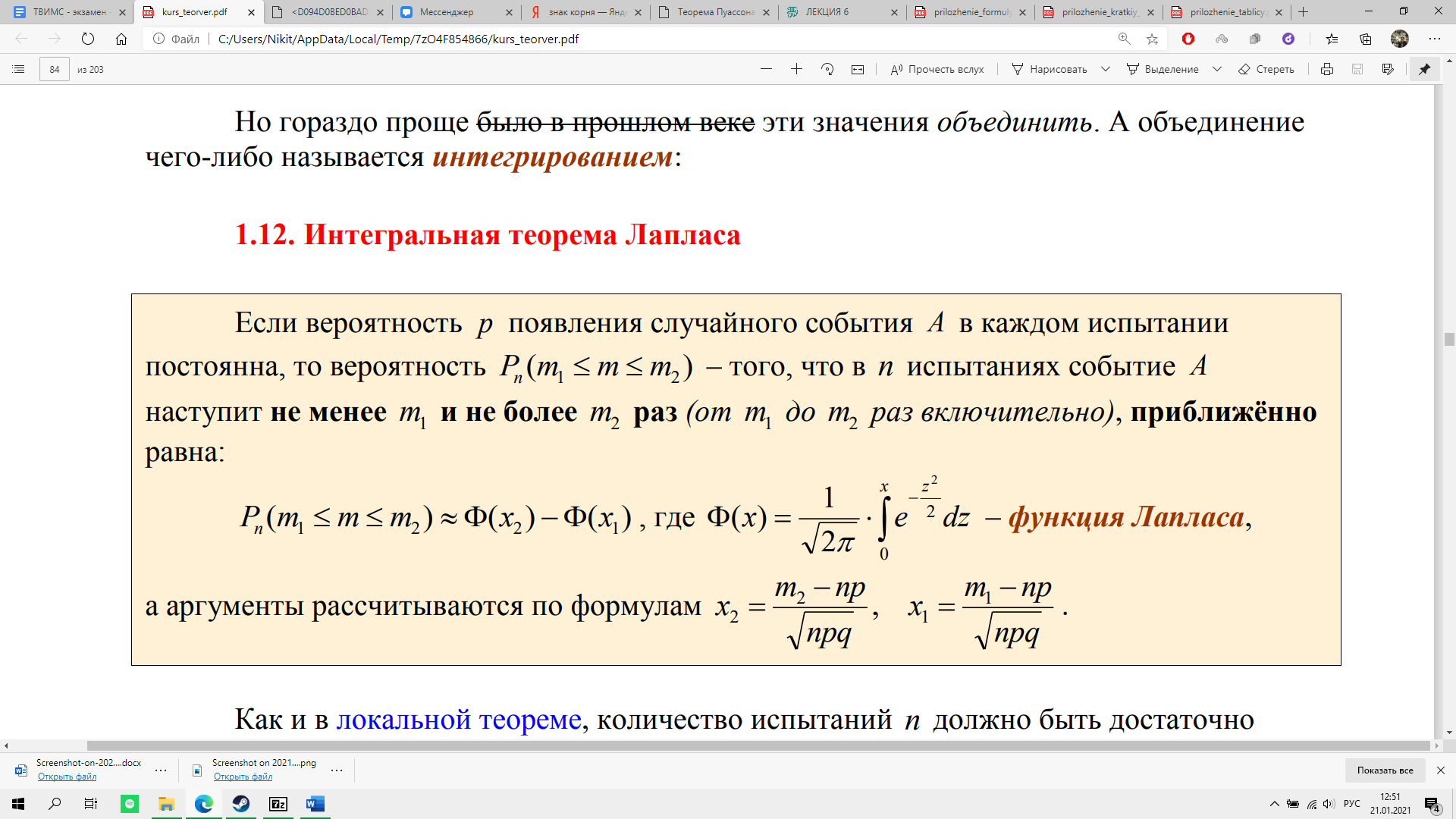
Как и в локальной теореме, количество испытаний n должно быть достаточно большим и вероятность p не слишком мала, и на практике следует ориентироваться на выполнение того же неравенства npq > 10 , в противном случае приближение к точному результату, полученному по Бернулли будет плохим.

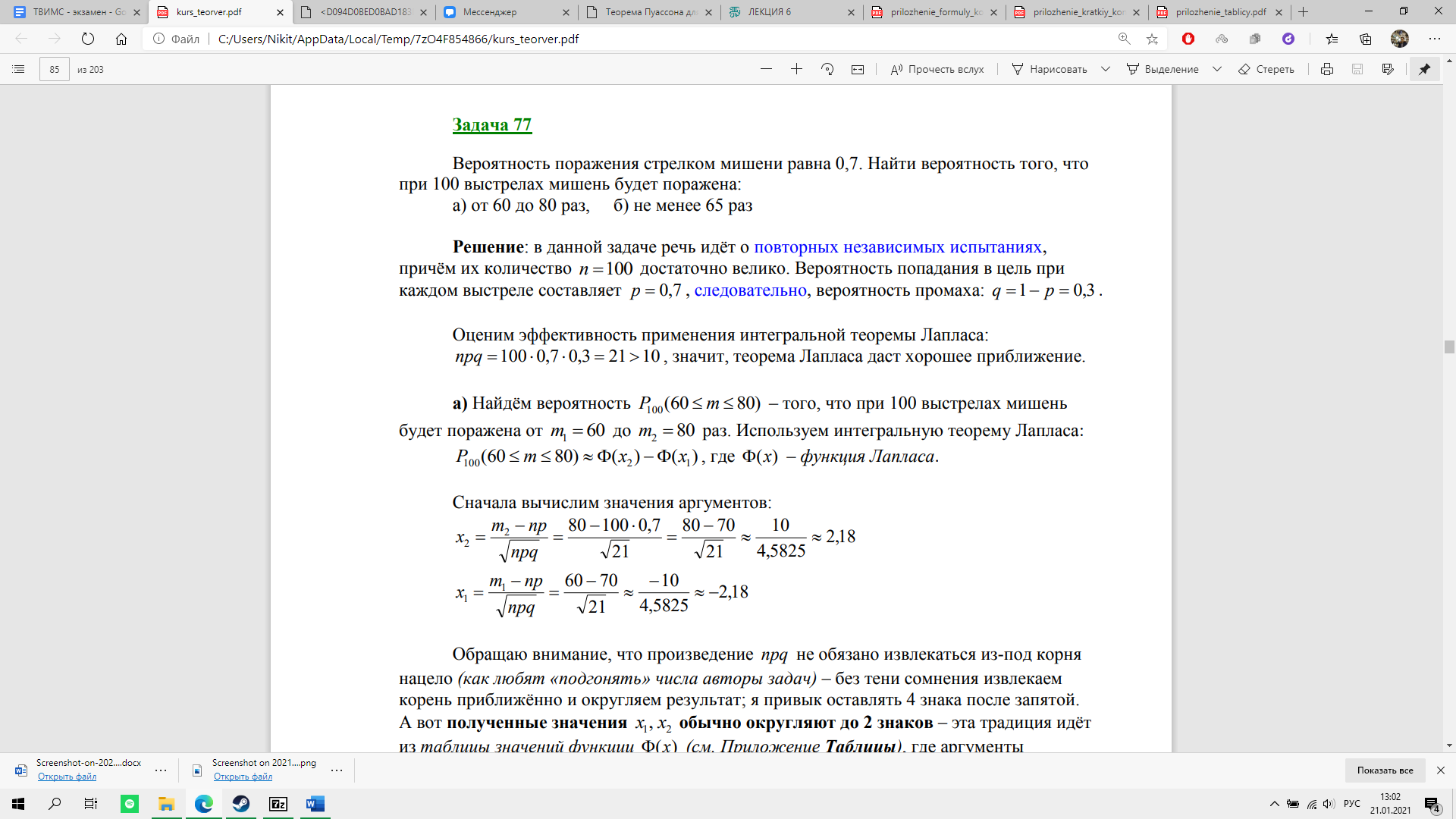
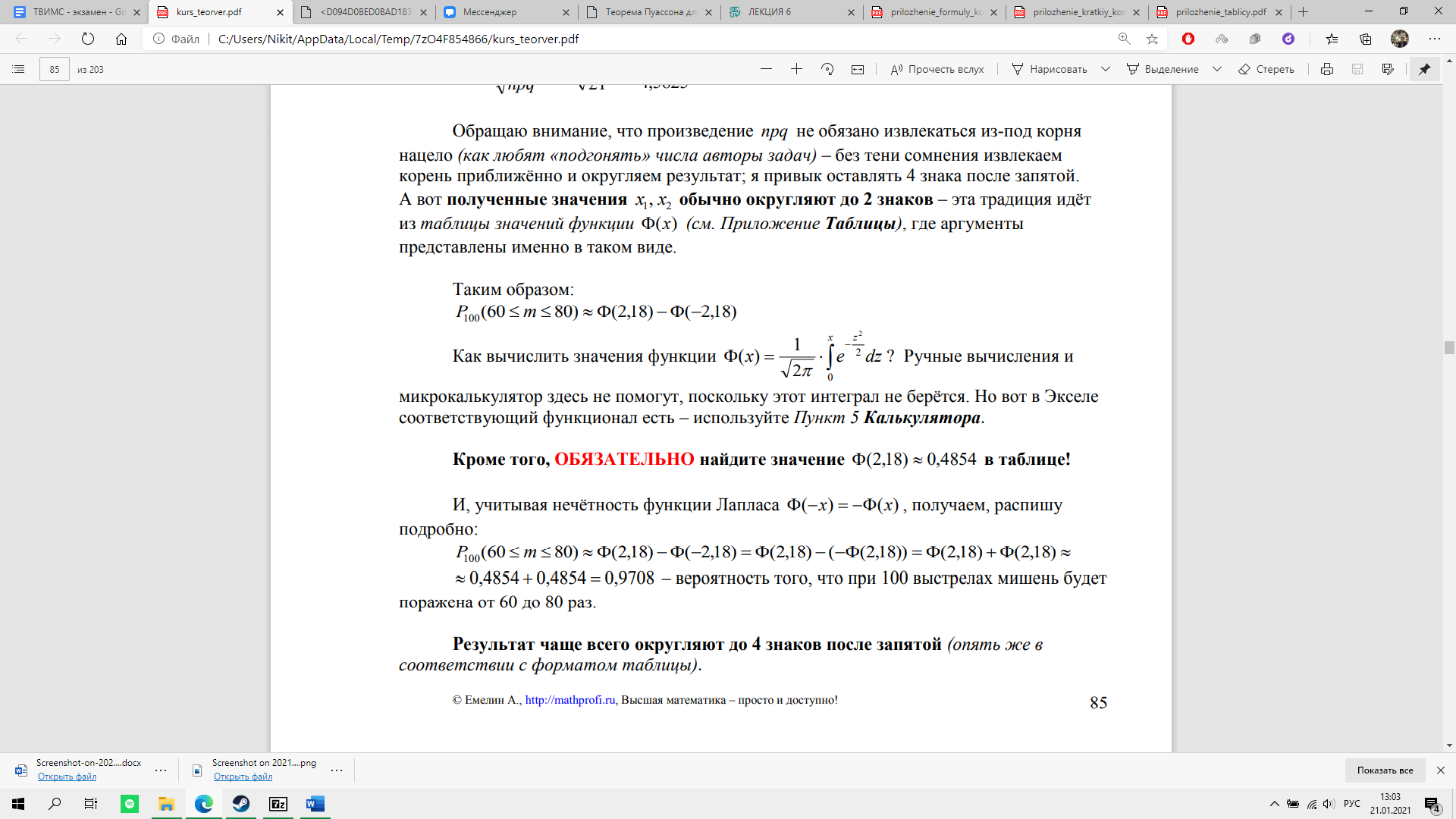
Пример. Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена:

а) от 60 до 80 раз, б) не менее 65 раз.

Решение: В данной задаче речь идёт о повторных независимых испытаниях, причём их количество (n = 100) достаточно велико. Вероятность попадания в цель при каждом выстреле составляет p = 0,7, следовательно, вероятность промаха: q = 1 - p = 0,3.

Оценим эффективность применения интегральной теоремы Лапласа: npq = 100*0,7*0,3 = 21 > 10, значит, теорема Лапласа даст хорошее приближение.

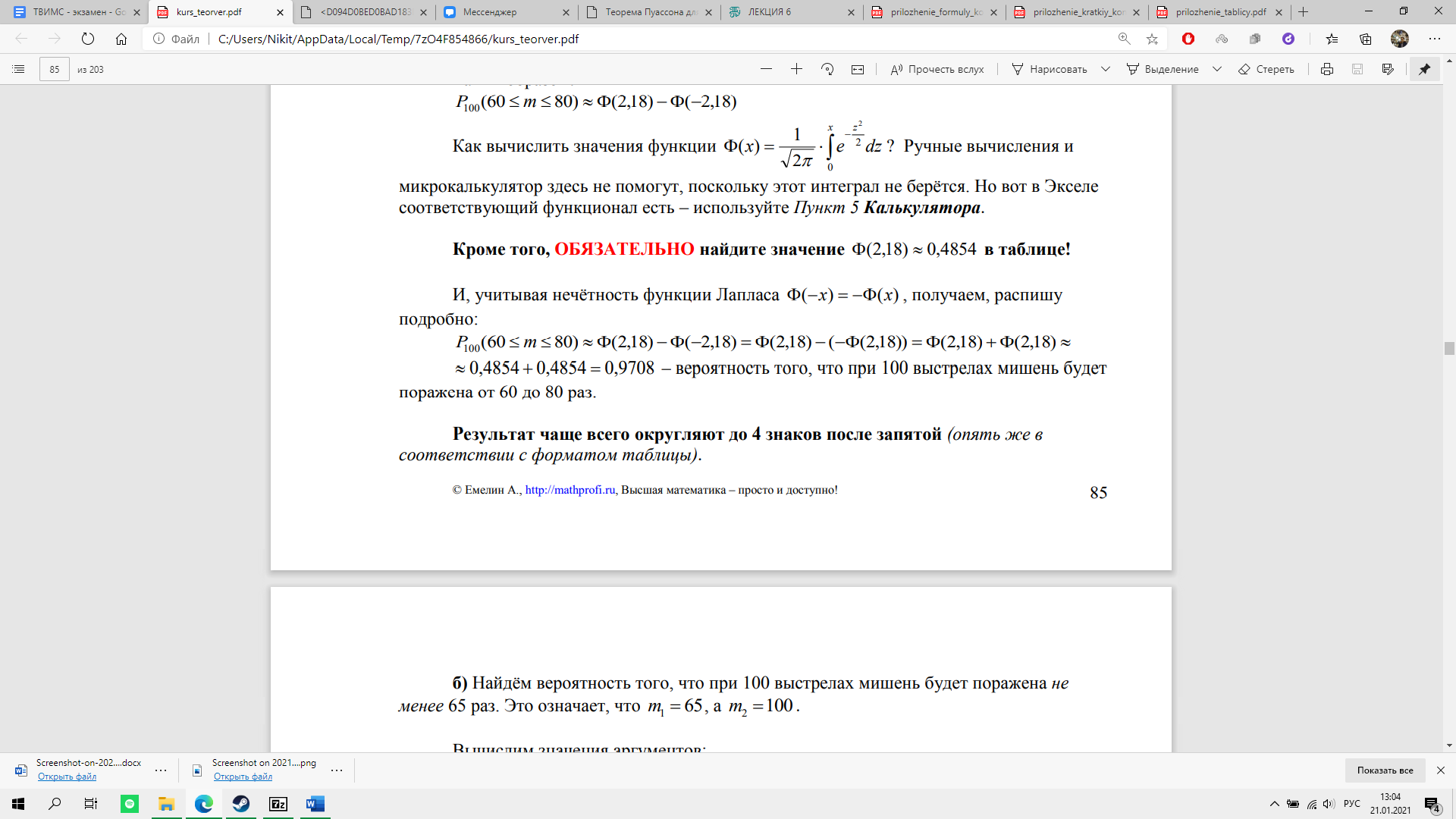
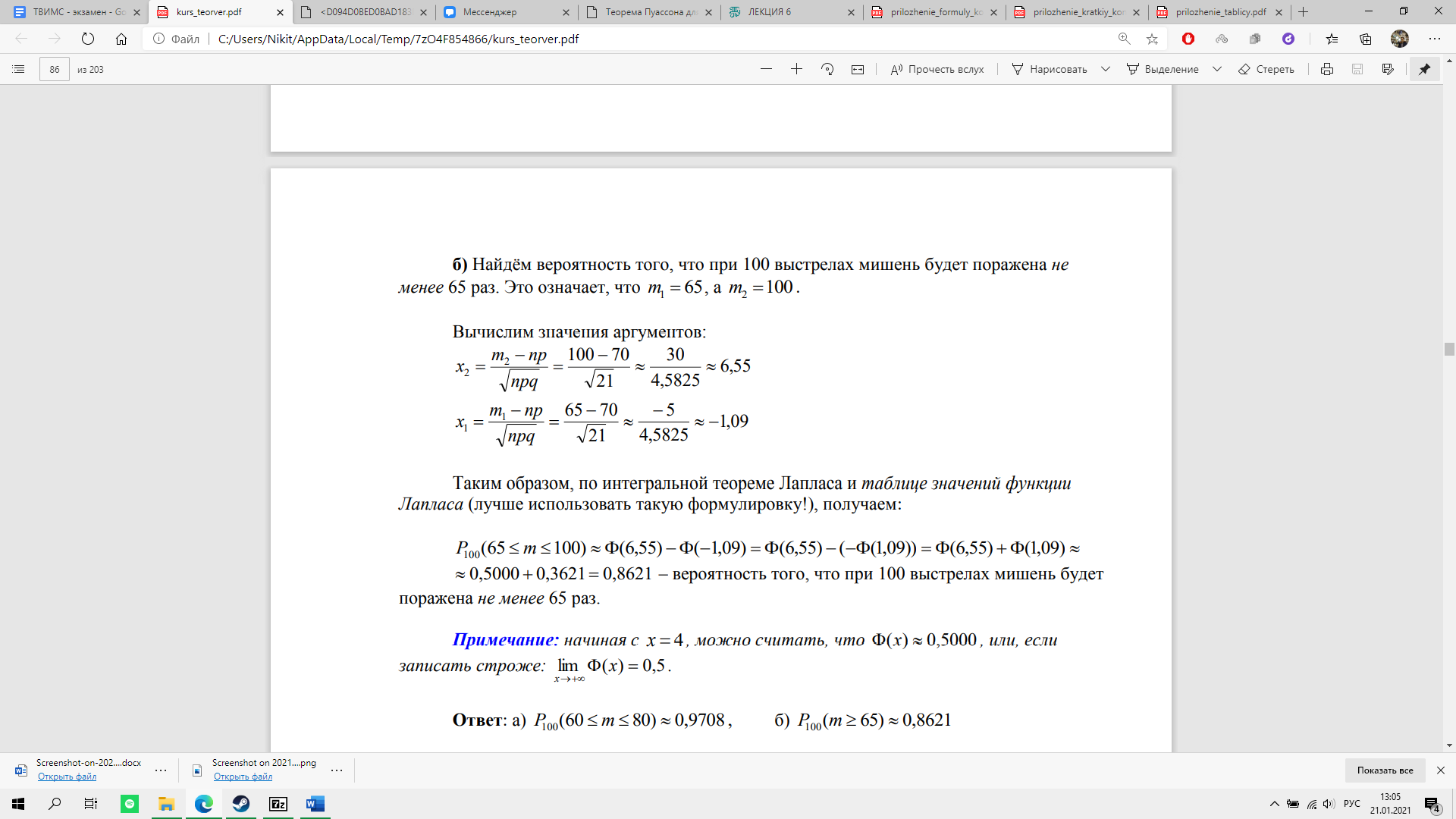
Отклонение относительной частоты от постоянной вероятности

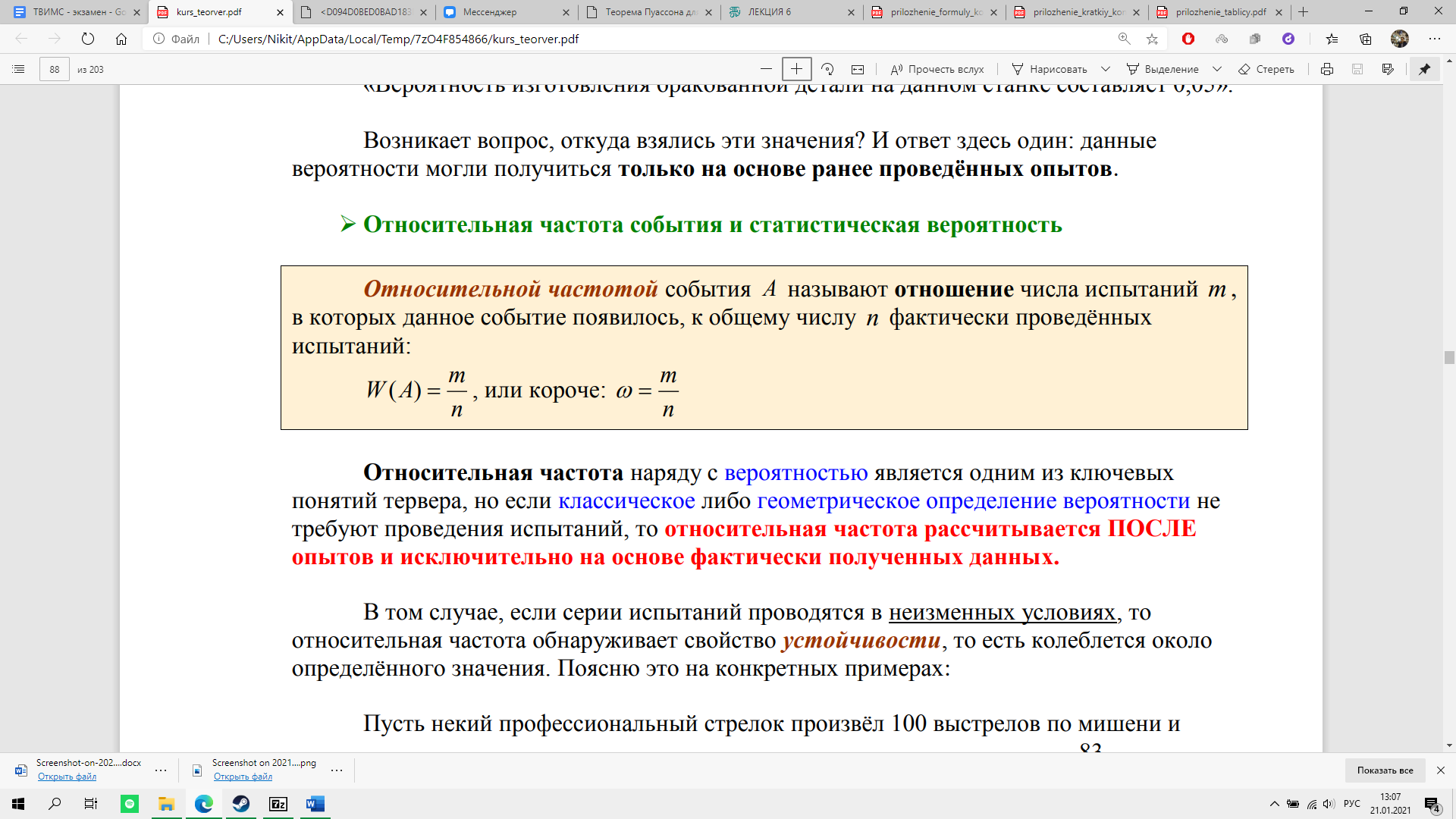
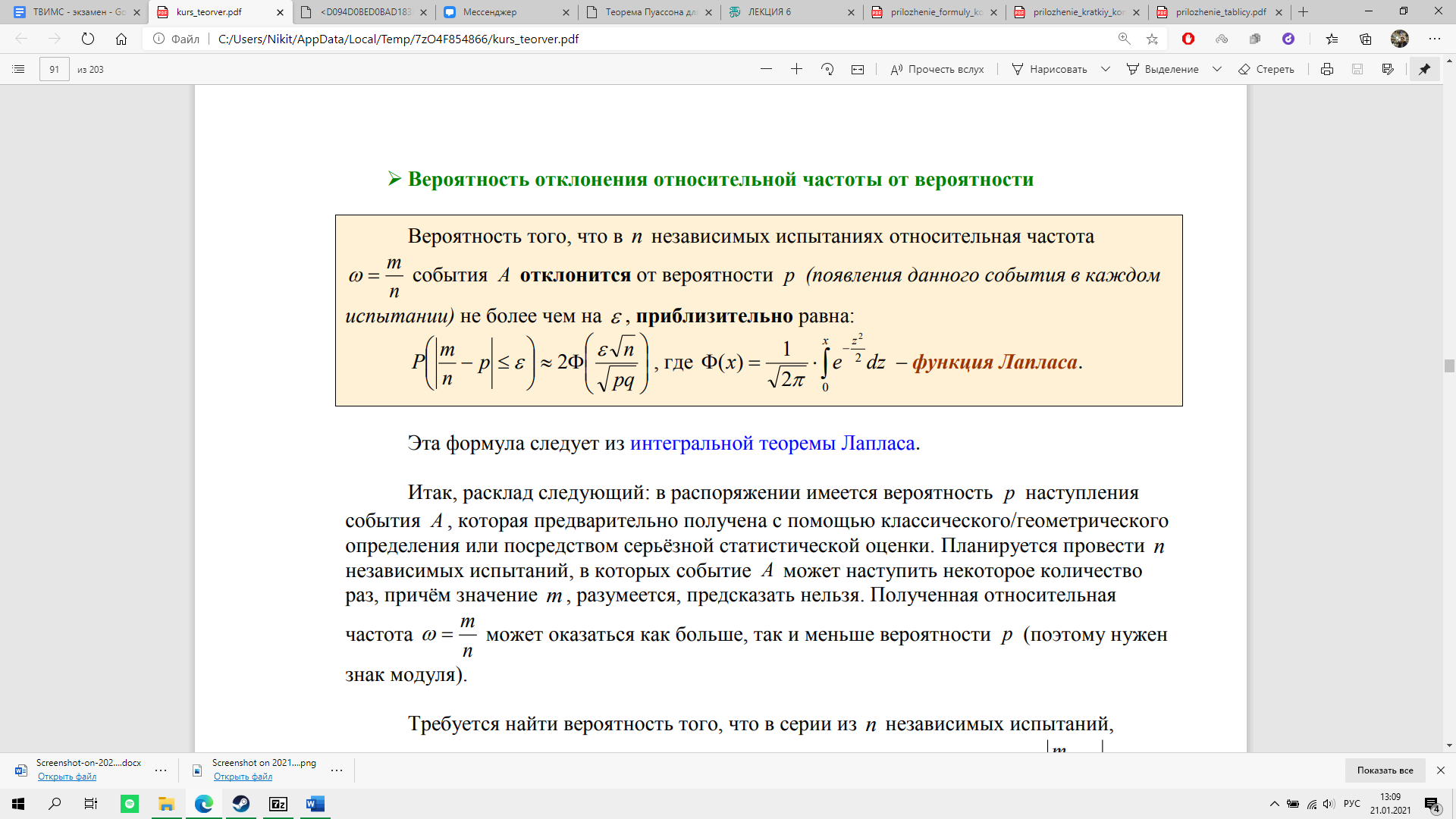
Эта формула следует из интегральной теоремы Лапласа.

Имеется вероятность p наступления события A , которая предварительно получена с помощью классического/геометрического определения или посредством серьёзной статистической оценки. Планируется провести n независимых испытаний, в которых событие A может наступить некоторое количество раз, причём значение m , разумеется, предсказать нельзя. Полученная относительная частота 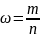может оказаться как больше, так и меньше вероятности p (поэтому нужен знак модуля).

Требуется найти вероятность того, что в серии из n независимых испытаний, расхождение между относительной частотой и теоретической вероятностью , будет не больше, чем заранее заданное число, например, не больше, чем .

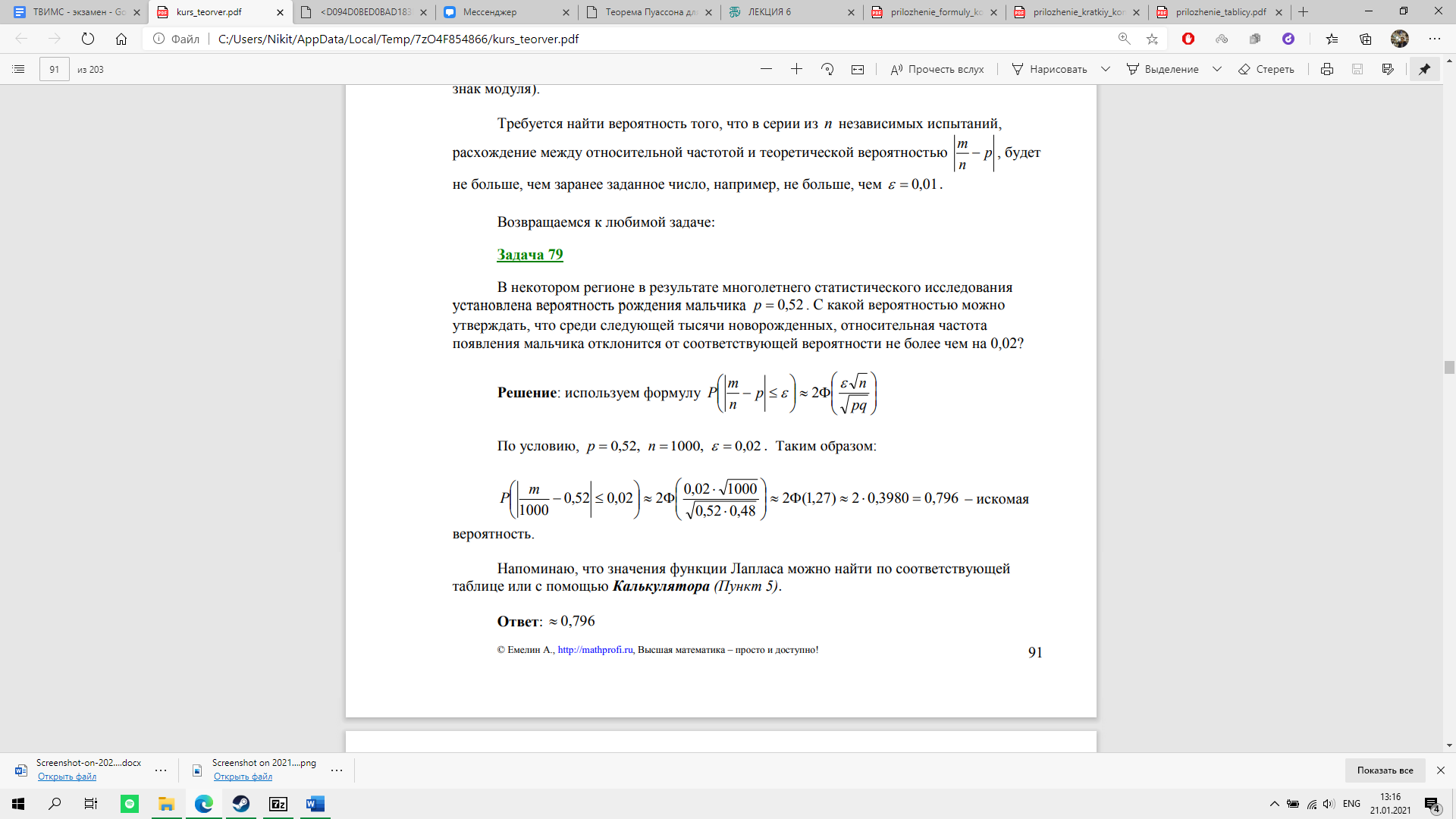
Пример. В некотором регионе в результате многолетнего статистического исследования установлена вероятность рождения мальчика p = 0,52 . С какой вероятностью можно утверждать, что среди следующей тысячи новорожденных, относительная частота появления мальчика отклонится от соответствующей вероятности не более чем на 0,02?

9. Дискретные случайные величины. Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения).

Случайной называют величину, которая может принимать одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретные случайные величины

Случайные величины делятся на дискретные и непрерывные.

Дискретная в данном случае означает, что случайная величина может принимать только лишь некоторые изолированные друг от друга значения.

Примерами дискретных случайных величин могут служить:

а) число успехов в серии испытаний Бернулли;

б) суммарное число очков, выпавшее на трех игральных костях;

в) количество пассажиров, прошедших через турникет станции метро за 1 минуту;

г) число попыток, необходимых студенту для успешной сдачи экзамена по теории вероятностей.

Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения)

Для того чтобы задать дискретную случайную величину, необходимо задать множество значений, которые она может принимать и соответствующие вероятности, с которыми она принимает эти значения, т.е. закон распределения дискретной случайной величины. Иными словами, законом распределения дискретной случайной величины называется соответствие между возможными значениями случайной величины и их вероятностями. Его можно задать таблично, аналитически и графически. Последовательность пар (𝑥1, 𝑝1), (𝑥2, 𝑝2), ⋯ , (𝑥𝑛, 𝑝𝑛) образует ряд распределения. В случаях, когда случайная величина может принимать конечное число значений, будем описывать закон распределения с помощью таблицы, которая будет рядом распределения дискретной случайной величины.

Ряд распределения:

X	x1	x2	x3	...	xn
P	p1	p2	p3	...	pn

Такая таблица означает, что случайная величина X принимает значение 𝑥1 с вероятностью 𝑝1, 𝑥2 с вероятностью 𝑝2 и т.д., 𝑥𝑛 с вероятностью 𝑝𝑛.

Другими словами, вероятность того, что случайная величина X принимает значение 𝑥𝑖 обозначается: 𝑃(𝑋 = 𝑥𝑖 ) = 𝑝𝑖 . Значения 𝑥1, 𝑥2, ⋯ , 𝑥𝑛 могут быть любыми числами, а на вероятности 𝑝1, 𝑝2, ⋯ , 𝑝𝑛, следует наложить естественные ограничения. Во-первых, как любая вероятность, они должны быть неотрицательными и не превышающими единицы: 0 ≤ 𝑝𝑖 ≤ 1. А во-вторых, их 3 сумма должна быть равна 1: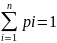 , поскольку случайная величина X достоверно принимает какое-то одно из своих возможных значений.

Таблицу распределения можно представить в виде полигона (многоугольника) распределения. Для этого просто соединяем отрезками точки (𝑥𝑖 , 𝑝𝑖) плоскости XOY:

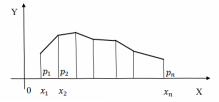
Пример: