5. Схема испытаний Бернулли.

Если производится несколько испытаний, при­чем вероятность события А в каждом испытании не за­висит от исходов других испытаний, то такие испытания называют независимыми относительно события А. В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность.

Ниже воспользуемся понятием сложного события, по­нимая под ним совмещение нескольких отдельных собы­тий, которые называют простыми.

Пусть производится n независимых испытаний, в каж­дом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность собы­тия A в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления со­бытия А в каждом испытании также постоянна и равна q =1 - р.

Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.

Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:

1. A — появление события A с вероятностью p;

2. «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.

Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.

Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:

Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:

где C_n^k — число сочетаний, q = 1 − p.

6. Теорема Пуассона.

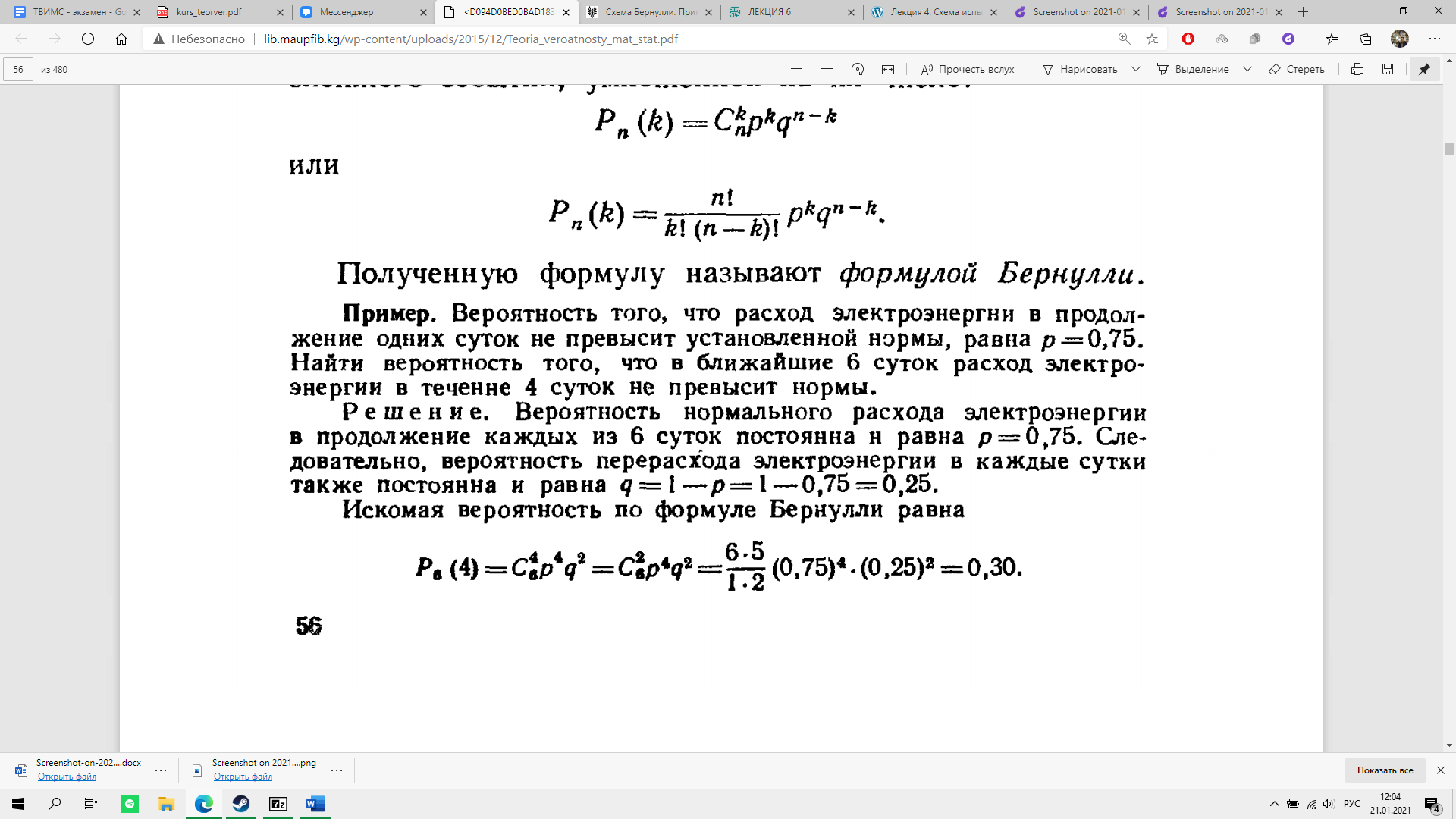
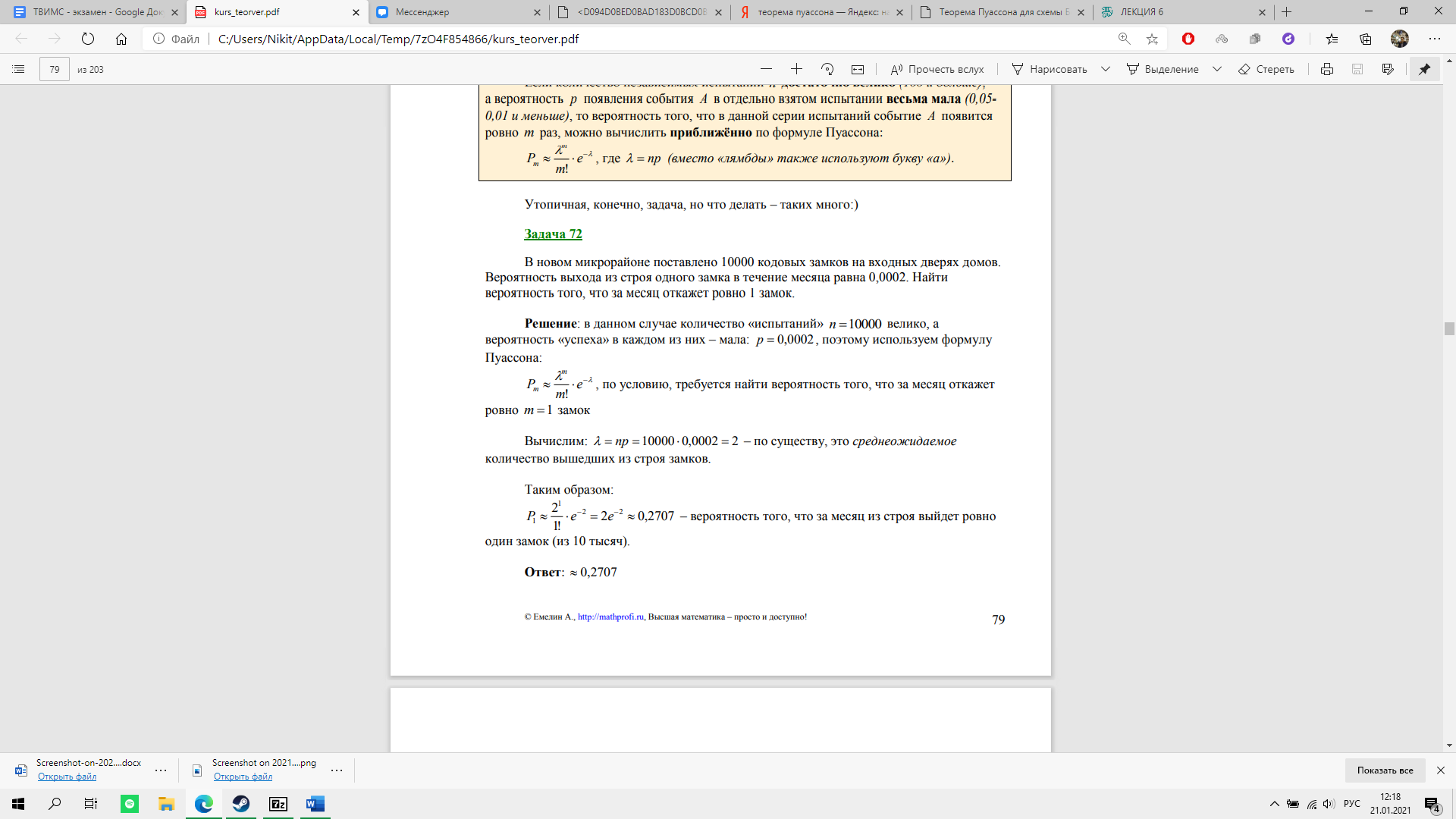
Если количество независимых испытаний n достаточно велико (100 и больше), а вероятность p появления события A в отдельно взятом испытании весьма мала (0,05- 0,01 и меньше), то вероятность того, что в данной серии испытаний событие A появится ровно m раз, можно вычислить приближённо по формуле Пуассона:

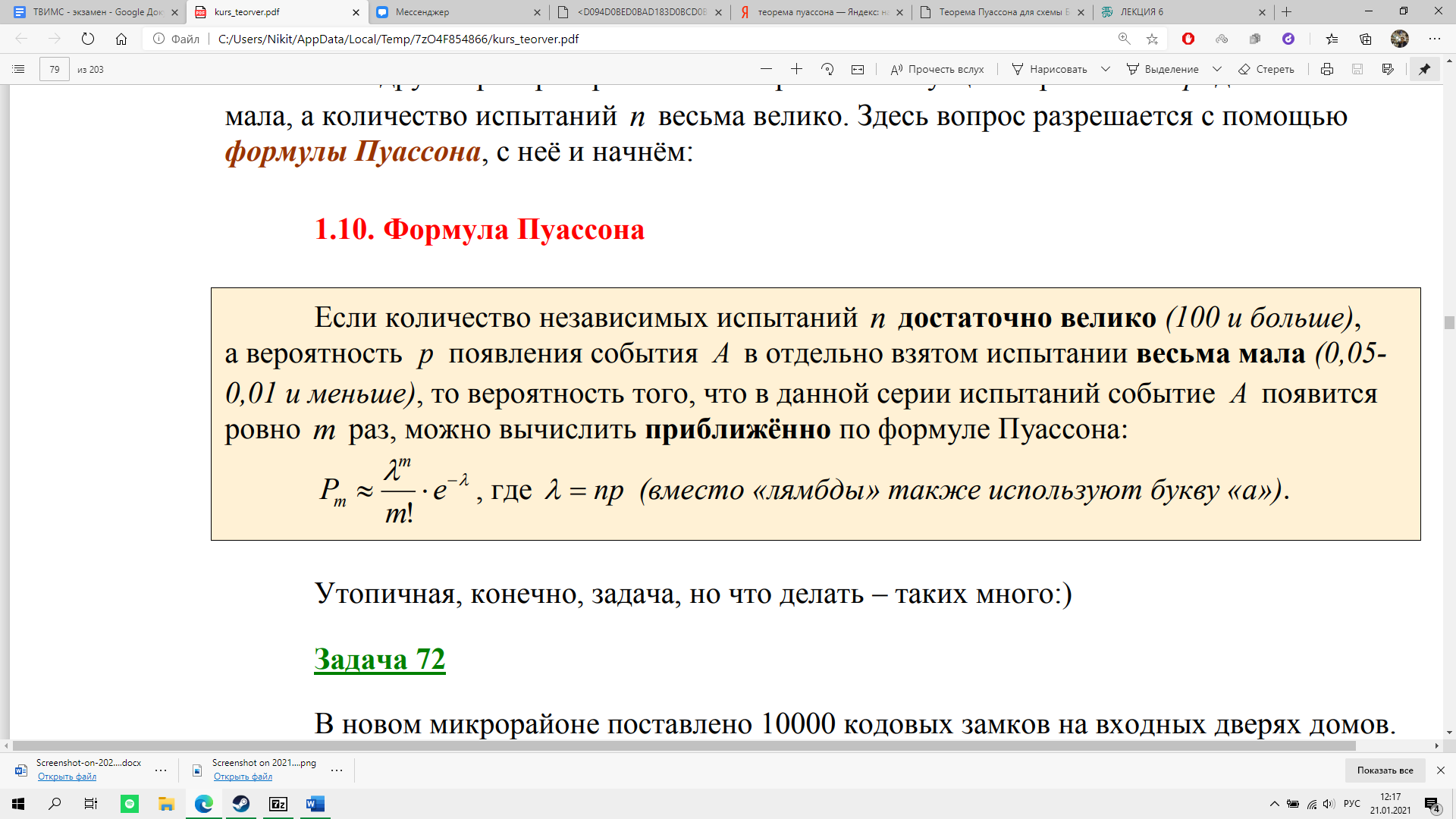
Пример:

http://old.exponenta.ru/educat/class/courses/tv/theme0/6.asp

7. Локальная теорема Лапласа.

Локальная теорема Лапласа и дает асимптотическую¹ формулу, которая позволяет приближенно найти вероятность появления события ровно к раз в п испытаниях, если число испытаний достаточно велико.

Заметим, что для частного случая, а именно для р = 1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра — Лапласа.

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции:

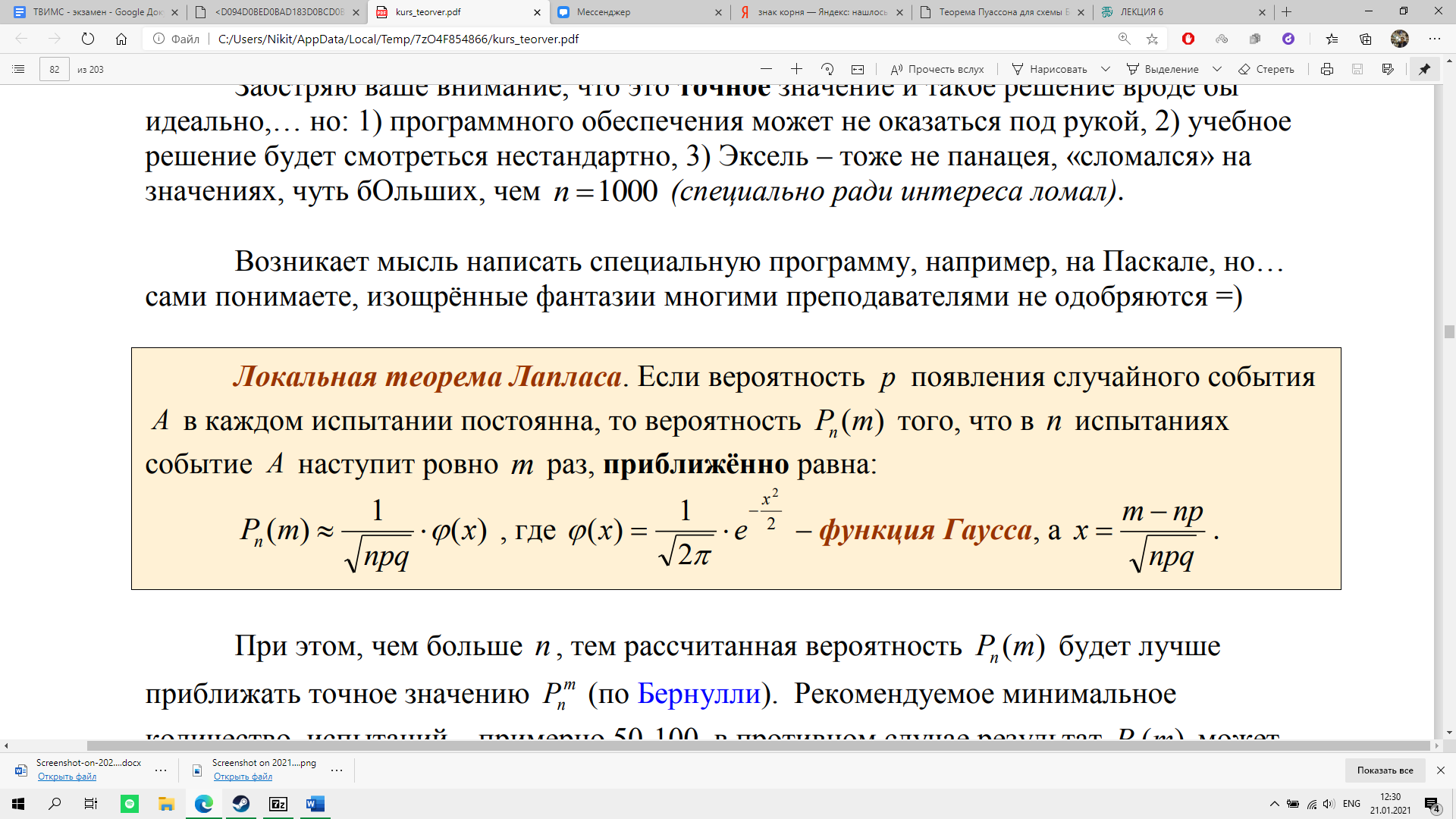
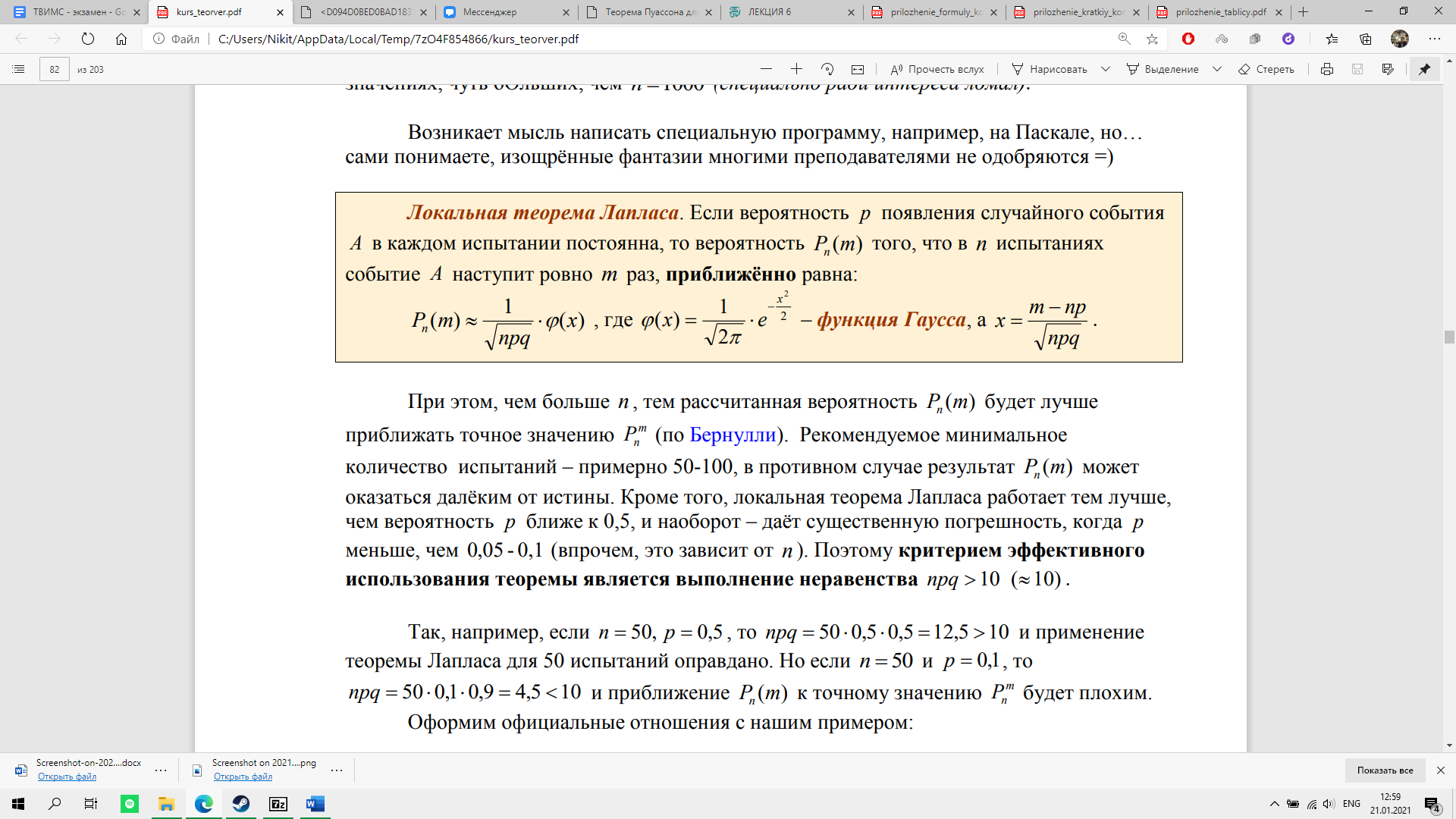
Пример. Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно: а) 200 раз, б) 225 раз.

Сначала распишем известные величины, чтобы они были перед глазами:

n = 400 – общее количество независимых испытаний;

p = 0,5 – вероятность выпадения орла в каждом броске;

q = 1 - p = 0,5 – вероятность выпадения решки.

а) Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно m 200 раз. Ввиду большого количества испытаний используем локальную теорему Лапласа:

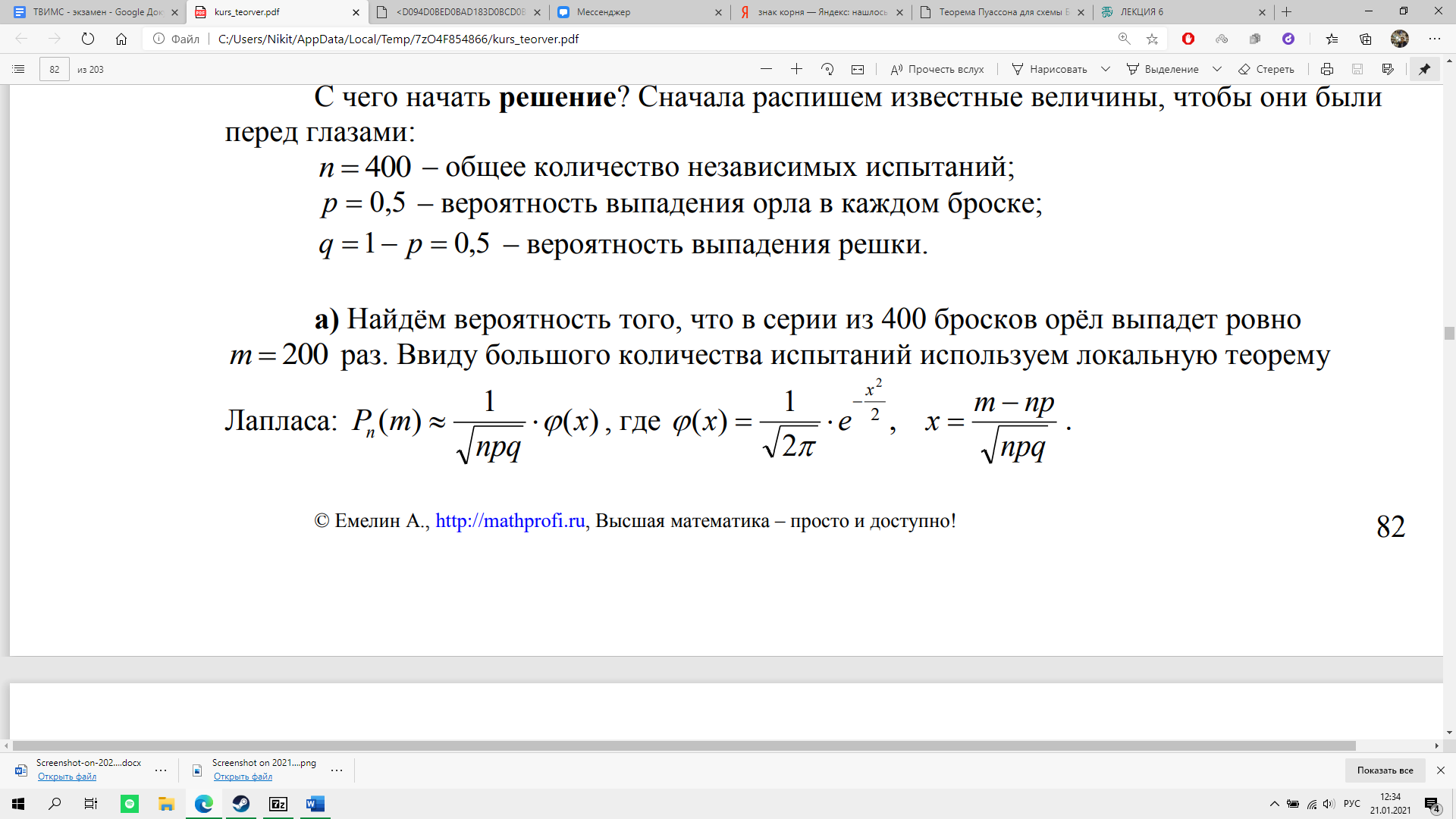
На первом шаге вычислим значение аргумента:

.

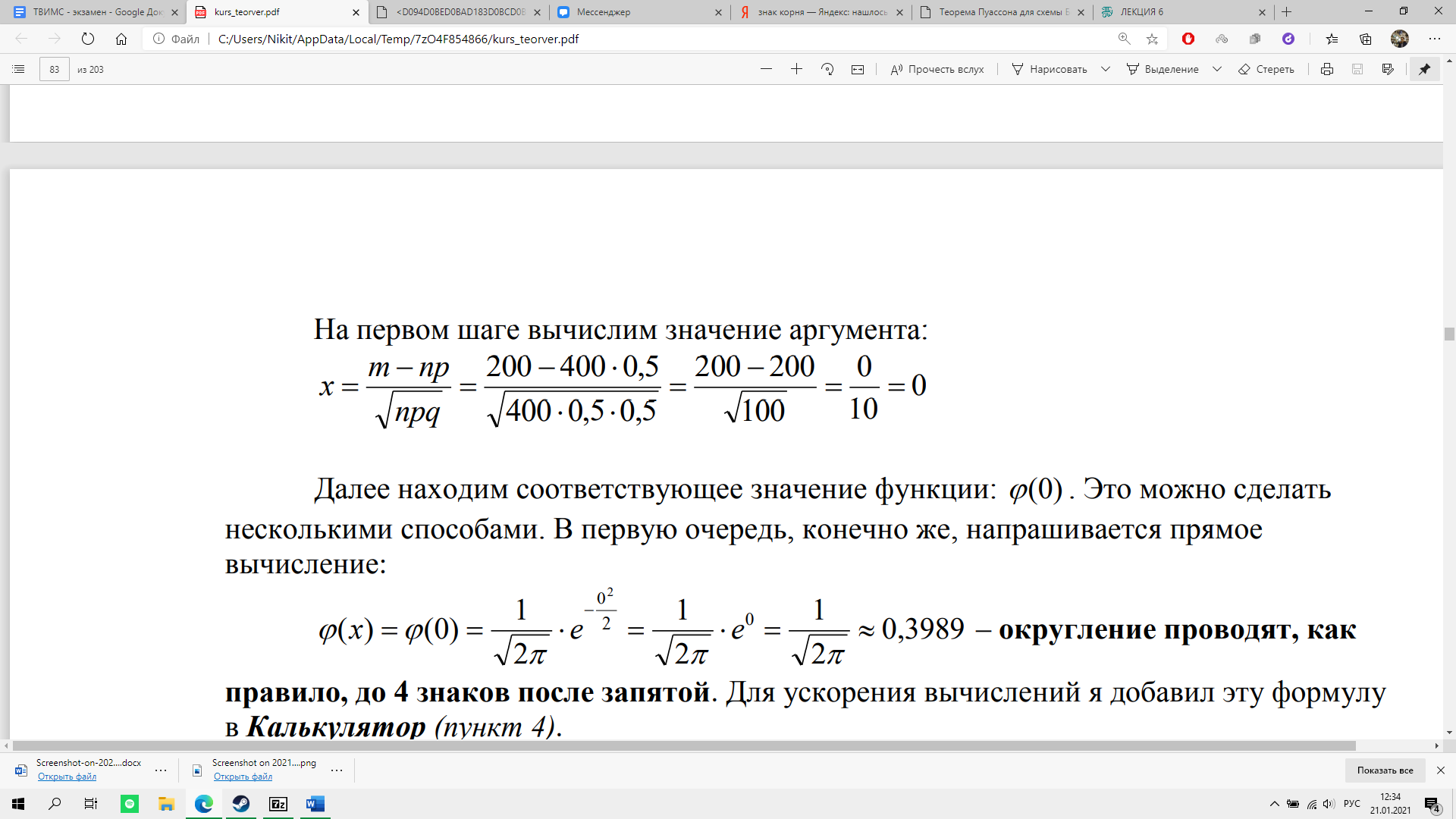Далее находим соответствующее значение функции: 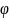(0) . Прямое вычисление:

.

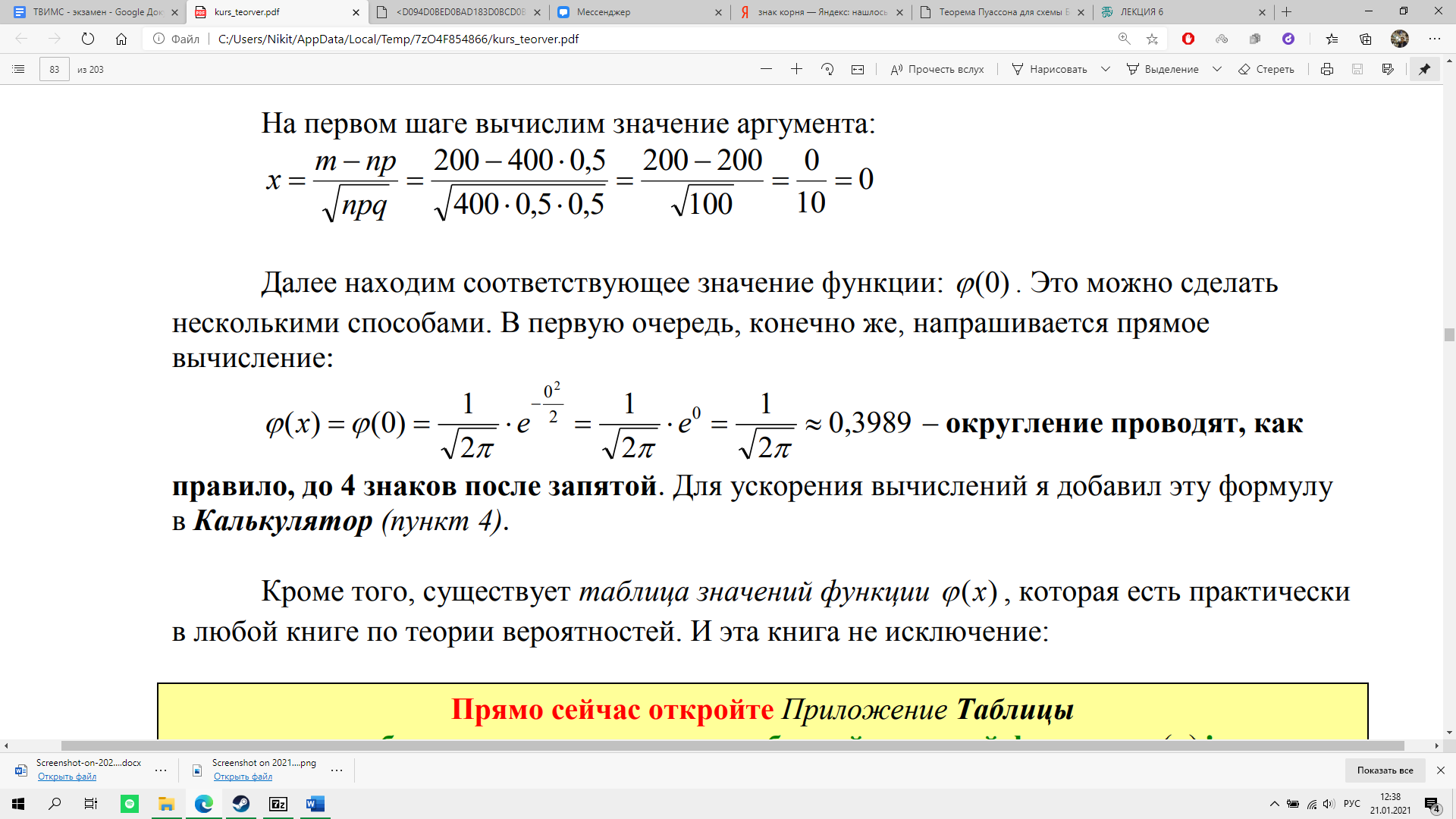На заключительном этапе применим формулу

- вероятность того, что при 400 бросках орёл выпадет ровно 200 раз.

Поиск 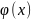осуществляется по таблице значений функции Гаусса.