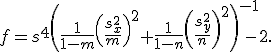- •2. События. Сумма событий, произведение, разность
- •Сумма событий, произведение, разность
- •3. Условная вероятность.
- •4. Формула полной вероятности, формула Байеса. Формула полной вероятности
- •Формула Байеса
- •5. Схема испытаний Бернулли.
- •6. Теорема Пуассона.
- •7. Локальная теорема Лапласа.
- •8. Интегральная теорема Лапласа. Отклонение относительной частоты от постоянной вероятности. Интегральная теорема Лапласа
- •Отклонение относительной частоты от постоянной вероятности
- •9. Дискретные случайные величины. Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения).
- •Дискретные случайные величины
- •Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения)
- •10. Функция распределения вероятностей и ее свойства. Функция распределения вероятностей
- •Свойства функции
- •11. Плотность распределения вероятностей и ее свойства.
- •12. Математическое ожидание и его свойства. Математическое ожидание
- •Свойства математического ожидания
- •13. Дисперсия и ее свойства. Среднеквадратическое отклонение. Дисперсия
- •Свойства дисперсии
- •Среднеквадратическое отклонение
- •Пример дисперсии
- •14. Мода. Медиана, начальные и центральные моменты. Мода
- •Медиана
- •Начальные и центральные моменты
- •15. Биномиальное распределение.
- •16. Распределение Пуассона.
- •17. Геометрическое распределение.
- •18. Непрерывные случайные величины. Плотность распределения. Функция распределения.
- •19. Числовые характеристики непрерывной случайной величины. Математическое ожидание
- •Дисперсия
- •20. Коэффициент асимметрии. Эксцесс.
- •25. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева.
- •26. Усиленный закон больших чисел, теорема Бернулли. Теорема Пуассона.
- •27. Центральная предельная теорема.
- •28. Многомерные случайные величины. Функция распределения и плотность распределения.
- •33. Задачи математической статистики.
- •34. Выборка. Типы выбора. Виды выбора. Свойства выбора.
- •35. Вариационный ряд и его свойства. Гистограмма
- •36. Эмпирическая функция распределения.
- •37. Выборочные числовые характеристики: выборочная средняя, выборочная дисперсия, исправленная выборочная дисперсия.
- •38. Точечное оценивание неизвестного параметра. Свойства оценок: состоятельность, несмещенность, эффективность.
- •39. Интервальные оценки. Доверительный интервал. Доверительный интервал для оценки математического ожидания нормально распределенной случайной величины.
- •40. Метод моментов.
- •41. Метод максимального правдоподобия.
- •42. Метод наименьших квадратов.
- •43. Проверка статистических гипотез. Ошибки первого и второго рода.
- •44. Критерий согласия Пирсона 𝜒2.
- •45. Критерий Стьюдента.
- •Сравнение выборочного среднего с заданным значением
- •Сравнение двух выборочных средних при известных дисперсиях
- •Сравнение двух выборочных средних при неизвестных равных дисперсиях
- •Сравнение двух выборочных средних при неизвестных неравных дисперсиях
- •Сравнение двух выборочных средних в связанных выборках
- •Сравнение разности средних с заданным значением
- •46. Точный критерий Фишера.
- •47. Непараметрический критерий Вилкоксона.
Сравнение двух выборочных средних при известных дисперсиях
Заданы
две выборки
![]() .
.
Дополнительные предположения:
обе выборки простые и нормальные;
значения дисперсий
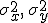 известны априори; это означает, что
дисперсии были оценены заранее не по
этим выборкам, а исходя из какой-то
другой информации; случай «неизвестных
дисперсий», когда такого источника
информации нет и дисперсии приходится
оценивать по самим выборкам, описан
ниже.
известны априори; это означает, что
дисперсии были оценены заранее не по
этим выборкам, а исходя из какой-то
другой информации; случай «неизвестных
дисперсий», когда такого источника
информации нет и дисперсии приходится
оценивать по самим выборкам, описан
ниже.
Нулевая
гипотеза
![]() (средние в двух выборках равны).
(средние в двух выборках равны).
Статистика критерия:
![]()
имеет
стандартное Нормальное
распределение
![]() ,
где
,
где
![]() — выборочные
средние.
— выборочные
средние.
Критерий (при уровне значимости ):
против альтернативы
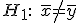
если
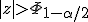 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
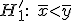
если
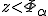 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
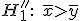
если
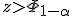 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
где
![]() есть
-квантиль
стандартного нормального распределения.
есть
-квантиль
стандартного нормального распределения.
Сравнение двух выборочных средних при неизвестных равных дисперсиях
Заданы две выборки .
Дополнительные предположения:
обе выборки простые и нормальные;
значения дисперсий равны:
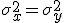 ,
но априори не известны.
,
но априори не известны.
Нулевая гипотеза (средние в двух выборках равны).
Статистика критерия:
![]()
имеет
распределение
Стьюдента
с
![]() степенями свободы, где
степенями свободы, где
![]() — выборочные
дисперсии;
— выборочные
дисперсии;
— выборочные средние.
Критерий (при уровне значимости ):
против альтернативы
если
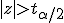 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
если
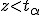 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
если
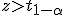 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
где есть -квантиль распределения Стьюдента с степенями свободы.
Сравнение двух выборочных средних при неизвестных неравных дисперсиях
Задача сравнения средних двух нормально распределённых выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. Точного решения этой задачи до настоящего времени нет. На практике используются различные приближения.
Заданы две выборки .
Дополнительное предположение: обе выборки простые и нормальные.
Нулевая гипотеза (средние в двух выборках равны).
Статистика критерия:
![]()
где
![]() — выборочные
дисперсии;
— выборочные
дисперсии;
— выборочные средние.
Критерий (при уровне значимости ):
против альтернативы
если
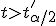 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
если
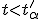 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
если
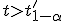 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
где
квантили
![]() определяются по-разному в различных
приближениях:
определяются по-разному в различных
приближениях:
Критерий Кохрена-Кокса:
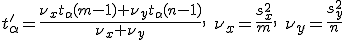 ,
где
,
где
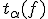 есть
-квантиль
распределения Стьюдента с
есть
-квантиль
распределения Стьюдента с
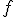 степенями свободы;
степенями свободы;Критерий Сатервайта:
есть -квантиль распределения Стьюдента с числом степеней свободы
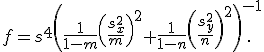
Критерий Крамера-Уэлча:
есть -квантиль распределения Стьюдента с числом степеней свободы