
- •2. События. Сумма событий, произведение, разность
- •Сумма событий, произведение, разность
- •3. Условная вероятность.
- •4. Формула полной вероятности, формула Байеса. Формула полной вероятности
- •Формула Байеса
- •5. Схема испытаний Бернулли.
- •6. Теорема Пуассона.
- •7. Локальная теорема Лапласа.
- •8. Интегральная теорема Лапласа. Отклонение относительной частоты от постоянной вероятности. Интегральная теорема Лапласа
- •Отклонение относительной частоты от постоянной вероятности
- •9. Дискретные случайные величины. Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения).
- •Дискретные случайные величины
- •Закон распределения дискретной случайной величины (ряд распределения, многоугольник распределения)
- •10. Функция распределения вероятностей и ее свойства. Функция распределения вероятностей
- •Свойства функции
- •11. Плотность распределения вероятностей и ее свойства.
- •12. Математическое ожидание и его свойства. Математическое ожидание
- •Свойства математического ожидания
- •13. Дисперсия и ее свойства. Среднеквадратическое отклонение. Дисперсия
- •Свойства дисперсии
- •Среднеквадратическое отклонение
- •Пример дисперсии
- •14. Мода. Медиана, начальные и центральные моменты. Мода
- •Медиана
- •Начальные и центральные моменты
- •15. Биномиальное распределение.
- •16. Распределение Пуассона.
- •17. Геометрическое распределение.
- •18. Непрерывные случайные величины. Плотность распределения. Функция распределения.
- •19. Числовые характеристики непрерывной случайной величины. Математическое ожидание
- •Дисперсия
- •20. Коэффициент асимметрии. Эксцесс.
- •25. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева.
- •26. Усиленный закон больших чисел, теорема Бернулли. Теорема Пуассона.
- •27. Центральная предельная теорема.
- •28. Многомерные случайные величины. Функция распределения и плотность распределения.
- •33. Задачи математической статистики.
- •34. Выборка. Типы выбора. Виды выбора. Свойства выбора.
- •35. Вариационный ряд и его свойства. Гистограмма
- •36. Эмпирическая функция распределения.
- •37. Выборочные числовые характеристики: выборочная средняя, выборочная дисперсия, исправленная выборочная дисперсия.
- •38. Точечное оценивание неизвестного параметра. Свойства оценок: состоятельность, несмещенность, эффективность.
- •39. Интервальные оценки. Доверительный интервал. Доверительный интервал для оценки математического ожидания нормально распределенной случайной величины.
- •40. Метод моментов.
- •41. Метод максимального правдоподобия.
- •42. Метод наименьших квадратов.
- •43. Проверка статистических гипотез. Ошибки первого и второго рода.
- •44. Критерий согласия Пирсона 𝜒2.
- •45. Критерий Стьюдента.
- •Сравнение выборочного среднего с заданным значением
- •Сравнение двух выборочных средних при известных дисперсиях
- •Сравнение двух выборочных средних при неизвестных равных дисперсиях
- •Сравнение двух выборочных средних при неизвестных неравных дисперсиях
- •Сравнение двух выборочных средних в связанных выборках
- •Сравнение разности средних с заданным значением
- •46. Точный критерий Фишера.
- •47. Непараметрический критерий Вилкоксона.
44. Критерий согласия Пирсона 𝜒2.
Критерий Пирсона, или критерий χ2(Хи-квадрат) - применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) для каждого из интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Число интервалов зависит от объема выборки.
Недостатком критерия согласия Пирсона является потеря части первоначальной информации, связанная с необходимостью группировки результатов наблюдений в интервалы и объединения отдельных интервалов с малым числом наблюдений. В связи с этим рекомендуется дополнять проверку соответствия распределений по критерию χ2 другими критериями. Особенно это необходимо при сравнительно малом объеме выборки (n ≈ 100).
Для проверки критерия вводится статистика:
![]()
Где:
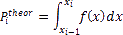 .
Предполагаемая вероятность попадания
в i-й
интервал;
.
Предполагаемая вероятность попадания
в i-й
интервал;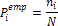 .
Соответствующее эмпирическое значение;
.
Соответствующее эмпирическое значение;ni. Число элементов выборки из i-го интервала.
Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ2.
Если полученная статистика превосходит квантиль закона распределения χ2 заданного уровня значимости α с (k - 1) или с (k - p - 1) степенями свободы, где k - число наблюдений или число интервалов (для случая интервального вариационного ряда), а p — число оцениваемых параметров закона распределения, то гипотеза H0 отвергается. В противном случае гипотеза принимается на заданном уровне значимости α.
45. Критерий Стьюдента.
t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называют гипотезой сдвига).
Все разновидности критерия Стьюдента являются параметрическими и основаны на дополнительном предположении о нормальности выборки данных. Поэтому перед применением критерия Стьюдента рекомендуется выполнить проверку нормальности. Если гипотеза нормальности отвергается, можно проверить другие распределения, если и они не подходят, то следует воспользоваться непараметрическими статистическими тестами.
Сравнение выборочного среднего с заданным значением
Задана
выборка
![]() .
.
Дополнительное предположение: выборка простая и нормальная.
Нулевая
гипотеза
![]() (выборочное среднее равно заданному
числу
(выборочное среднее равно заданному
числу
![]() ).
).
Статистика критерия:
![]()
имеет
распределение
Стьюдента
с
![]() степенями свободы, где
степенями свободы, где
![]() — выборочное
среднее,
— выборочное
среднее,
![]() — выборочная
дисперсия.
— выборочная
дисперсия.
Критерий
(при уровне
значимости
![]() ):
):
против альтернативы
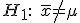
если
 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы
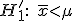
если
 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
против альтернативы

если
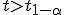 ,
то нулевая гипотеза отвергается;
,
то нулевая гипотеза отвергается;
где
![]() есть
есть
![]() -квантиль
распределения Стьюдента с
степенями свободы.
-квантиль
распределения Стьюдента с
степенями свободы.
