1.2. Законы алгебры Буля. Дистрибутивный, коммутативный, ассоциативный.

Переместительный (коммутативный) закон. Закон справедлив как для конъюнкции, так и для дизъюнкции.

х₁ + х₂ + х₃ + х_{4 .}= х₄ + х₃ + х₂+ х₁ - от перемены мест логических слагаемых сумма не меняется.

х₁ х₂ х₃ х_{4 .}= х₄ х₃ х₂ х₁ - от перемены мест логических сомножителей их произведение не меняется.

Этот закон справедлив для любого количества логических операндов.

Распределительный (дистрибутивный) закон.

(х₁ + х₂) х₃ = х₁ х₃ + х₂ х₃.

(х₁ + х₂) (х₁ + х₃) = х₁ + х₂ х₃.

Сочетательный (ассоциативный) закон. Закон справедлив как для конъюнкции, так и для дизъюнкции.

х₁ + х₂ + х₃ + х_4.= (х₂ + х₃)+ х₁ + х_4.=(х₁ + х₄ )+ (х₂ + х₃) - при логическом сложения отдельные слагаемые можно заменить их суммой.

х₁ х₂ х₃ х_4.= (х₂ х₃) х₁х₄=(х₁ х₄) (х₂ х₃) - при логическом умножении отдельные логические сомножители можно заменить их произведением.

1.3. Законы алгебры Буля. Поглощения, двойного отрицания, исключения.

Поглощения:

Двойного отрицания:

Исключения:

1.4. Законы алгебры Буля. Де Моргана, идемпотентности.

Закон Де Моргана

Используя законы де Моргана, можно выразить конъюнкцию через дизъюнкцию и три отрицания. Аналогично можно выразить дизъюнкцию:

Отрицание конъюнк­ции эквивалентно дизъюнкции отрицаний. Закон работает аналогично в обратном направлении.

Законы идемпотентности

Законы идемпотентности говорят о том, что в алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых "сомножителей" равносильна одному из них. Дизъюнкция одинаковых "слагаемых" равносильна одному из них.

1.5. Условное графическое обозначение логических элементов (стандарты).

1.6. Способы минимизации логических функций. Правило составления карты Карно.

Если хотите уверенно разбираться в этом вопросе советую посмотреть ролик на 50 мин. https://www.youtube.com/watch?v=wIEiX9R0SoE (вся важная информация до 35-40 мин.), но если времени не много вот небольшая инструкция по тому как пользоваться картой Карно.

1. Карта Карно для:

2 переменных

3 переменных

4 переменных

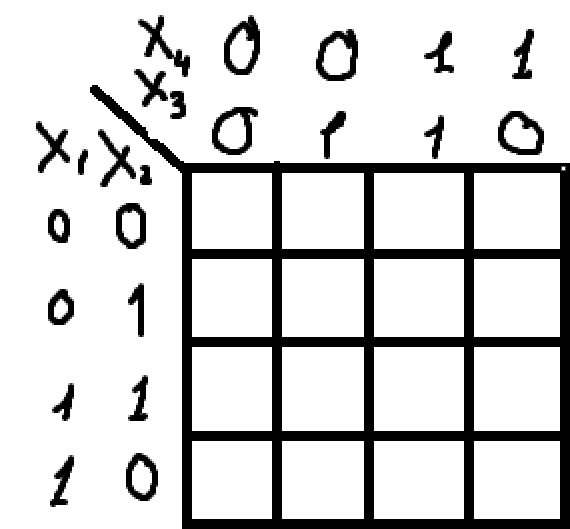
2. Определяем формат минимизации функции:

ДНФ (дизъюнктивная нормальная форма) использовать 1 для обводки контура

или

КНФ (конъюнктивная нормальная форма) использовать 0 для обводки контура

3. Выделяем контуры (обводим клетки количество которых равно 2⁰ или 2¹ или 2² или …) на карте Кано

Пример для ДНФ:

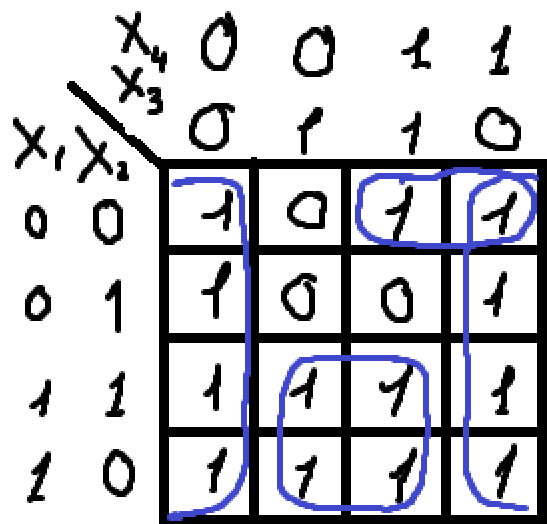
4. Для каждого контура выделяем области:

5. Смотрим на значения каждого х, на выбранной области, и записываем х, если значения равны только 1 и ¬х если значения равны только 0, а если значения равны 0 и 1, то данный х не записываем. (для ДНФ)

Между х в одном контуре ставиться ⋅ (умножение или И)

Между контурами ставиться + (сложение или ИЛИ)

Смотрим на значения каждого х, на выбранной области, и записываем х, если значения равны только 0 и ¬х если значения равны только 1, а если значения равны 0 и 1, то данный х не записываем. (для КНФ)

Между х в одном контуре ставиться + (сложение или ИЛИ)

Между контурами ставиться ⋅ (умножение или И)

Для примера из 3) была бы СДНФ (совершенная дизъюнктивная нормальная форма) такая:

F = ¬х1⋅¬х2⋅х4 + ¬х3 + х1⋅х3