1.30. Команды переходов в программе, особенности.
Эти команды занимают в оперативной памяти 3 байта и выполняются за 3 машинных цикла (10 тактов). Во всех этих командах применяется прямая адресация.
При выполнении команды перехода изменяется содержимое счетчика команд PC. Содержимое второго и третьего байтов команды перехода пересылается автоматически в счетчик команд во время фазы выполнения. Тогда при очередном цикле выборки МП извлекает команду из области памяти, на которую указывает 2-й и 3-й байты команды перехода. Таким образом, происходит переход в другую точку программы. Теперь выполняются одна за другой команды новой последовательности. Это продолжается до тех пор, пока не будет опять выполнена команда перехода.
а) Переход безусловный
JMP Адрес <PC> <B3><B2>B1
B2 мл. байт адреса
B3 ст. байт адреса
После этой команды выполнение программы продолжается с новой исходной точки, т.е. с адреса, содержащегося в байтах В2 и ВЗ команды перехода.
б) Переходы условные
(PC) <B3><B2>, если проверяемое условие выполняется; в противном случае PC (PC )+3, т.е. выполняется следующая команда после команды условного перехода
В1 ССС
B2 мл. байт адреса
B3 ст. байт адреса
Значение разрядов ССС команда выбирается в зависимости от проверяемого условия. В МП К580 имеется возможность делать переходы в зависимости от результата проверки следующих условий:
Команда перехода Проверяемое условие Значение ССС
JNZ Адрес (Tz) = 0
JZ Адрес (Tz) = 1
JNC Адрес (Tc) = 0
JC Адрес (Tc) = 1
JPO Адрес (Tp) = 0
JPE Адрес (Tp) = 1
JP Адрес (Ts) = 0
JM Адрес (Ts) = 1
Часть II.
2.1. Доказать следующие законы: дистрибутивный, поглощения.
Закон дистрибутивности:
(1)
(2)
Док-во: (1)
Если
И
И
ИЛИ
ИЛИ
При этом смотрите на диаграмму, визуально легче.
Док-во: (2)
Если x∈А∪(В∩С) → x∈ A или (х∈В и х∈С) → (x∈A или х∈В) и (x∈A или x∈С) → x∈(A ∪ В) ∩ (A ∪ С)
На диаграмме хз как представить x∈(A ∪ В) ∩ (A ∪ С)
Закон поглощения:
(Доказывается проще всего таблицей истинности)
A v (A & B)=A
Док-во:
A & (AvB)=A
Док-во:
2.2. Доказать следующие законы: идемпотентности, двойного отрицания.
Закон идемпотентности:
Док-во:
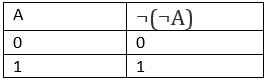
Двойное отрицание
Док-во:
2.3. Доказать следующий законы: исключения, коммутативный.
Закон исключения третьего:
Пусть А = “Сократ смертен”, тогда ¬А = “Сократ бессмертен”. Третьего не дано(это и есть этот закон и его доказательство)
Закон коммутативности:
A
В=В
A;
A&B=B&A.
Док-во:
2.4. Доказать следующий законы: Де Моргана, ассоциативный.
2.5. Произвольной функции используя законы алгебры Буля изменить базис на И-НЕ.
2.6. Произвольной функции ййиспользуя законы алгебры Буля изменить базис на ИЛИ-НЕ.
см 2.5
2.7. Преобразовать произвольную функцию в схему по УГО.
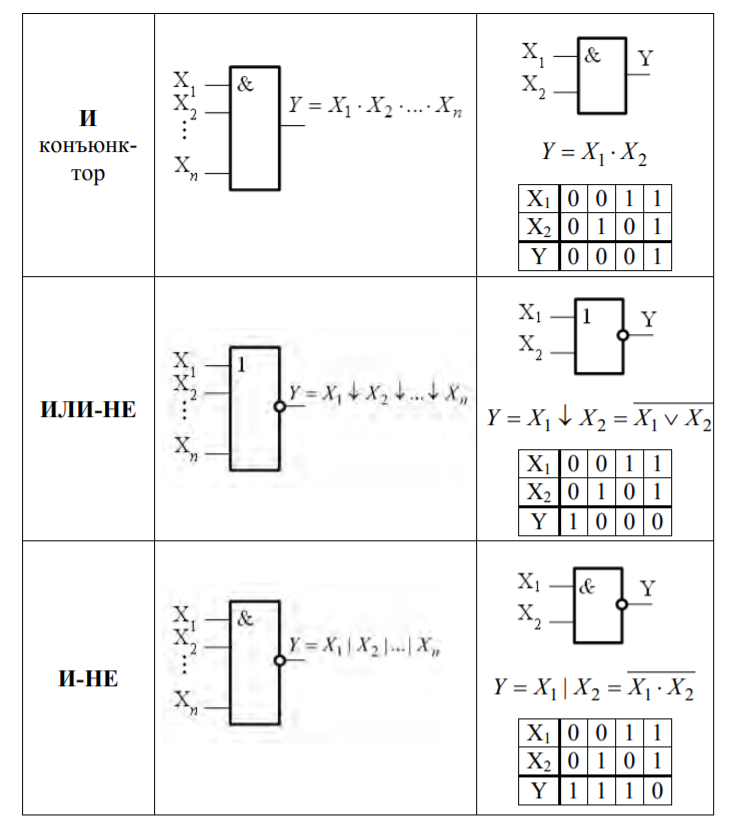
2.8. Преобразовать произвольную схему по УГО в функцию.
СМ. 2.7
2.9. Минимизировать произвольную логическую функцию с помощью карты Карно.
Правило составления карты Карно было описано в пункте 1.6, также можно посмотреть короткую(10 минут) лекцию https://www.youtube.com/watch?v=a37anDvo0bs
Рассмотрим построение карты Карно на примере следующей функции:
Построим таблицу истинности.
Запишем данные из таблицы истинности в карту Карно и выделяем области, содержащие единицы. Количество единиц должно равняться степени двойки.
В первой(синей) области X1 меняет своё значение, а X2 И X3 остаются неизменными, поэтому из первой области получаем выражение X2X3
Во второй области(красной) X1 и X3 сохраняют свои значения, а X2 меняется, поэтому получаем выражение X1X3
В третьей(зеленой) области значения сохраняют X1 и X2, X3 меняется, поэтому получаем выражение X1X2
После этого складываем полученные три выражения:
Если составить таблицу истинности для получившегося выражения, то она будет совпадать с той, что была построена для исходного выражения. Таким образом, эквивалентно
2.10. Минимизировать произвольную логическую функцию с помощью диаграмм Вейча.
2.11. Каскадное подключение дешифраторов, увеличение разряда дешифратора на n.
http://cifra.studentmiv.ru/wp-content/uploads/2013/07/E%60SA_Tema-5_Kaskad-deshifratorov.pdf
2.12. Каскадное подключение демультиплексора, увеличение разряда демультиплексора на n.
2.13. Реализовать RS триггер на элементах ИЛИ-НЕ.
(/
- отрицание)
Режим S=0, R=0 называют режимом хранения информации, так как информация на выходе остается неизменной.
При S=R=1 состояние триггера будет неопределенным, так как во время действия информационных сигналов логические уровни на выходах триггера одинаковы (Qn+1=/Qn+1=0), а после окончания их действия триггер может равновероятно принять любое из двух устойчивых состояний. Поэтому такая комбинация S=R=1 является запрещенной .