Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4613 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Московский технический университет связи и информатики
Предмет:
Математическая логика и теория алгоритмов
Файл:

КарКарФунСхемМнЖег (1)

.pdf
Скачиваний:
1
Добавлен:
01.04.2022
Размер:
458.8 Кб
Скачать
☆

Дискретная математика

Тема: Бинарные (булевы) функции

(Под)тема 2: Минимизация бинарной функции методом карты Карно

•Карта Карно – способ минимизации бинарной функции, заданной СДНФ или таблицей истинности.

•Минимизация функции – это её представление с возможно меньшим числом термов.

•Терм – значение переменной в аналитическом задании функции.

•Например 1.

f(x,y,z)=

x

 

У этой функции

y z x

7 термов:

y x z

 

x, y , z, x ,

y,x, z

•Сложность данного представления функции равна 7 (числу термов в представлении функции).

•Задача минимизации - уменьшение сложности функции.

•Карта Карно таблица, заголовки которой по горизонтали и вертикали – все возможные варианты максимальных конъюнкций термов.

•ВАЖНО! Соседние элементы заголовков должны иметь только одно отличие.

•Заполняется карта 1-цами или + или любым др. знаком на пересечении

конъюнкций, соответствующих слагаемому СДНФ функции.

•

• Пример 2.

Минимизируйте логическую функцию f()=V(0, 1, 4, 5) .

Решение.

СДНФ данной функции –

f ( x, y,z )=x y z x y z x y z x y z

 

 

 

 

 

 

 

x y z x y z x y z x y z =

 

 

 

 

 

z xyz .

 

xy

z xyz xy

Сложность данного представления функции равна 12.

Заполним для неё карту Карно.

=

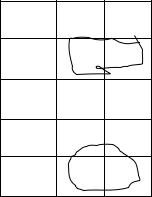
x y

x y

x y x y

z z

1 1

1 1

Заполненные единицами ячейки 1-й и последней строки, а также 1-го и последнего столбца являются соседними. Поэтому они по свойству дистрибутивности логического умножения относительно логического сложения объединяются следующим образом:

Элементы 1-ой строки

x y z x y z x y ( z z ) x y T x y .

Аналогично объединяются элементы последней строки x y z x y z x y

Полученные результаты объединяются x y x y y , как элементы соседних строк 1-й и последней.

Таким образом, функция сложности 12 превратилась в функцию сложности 1.

Ответ. Минимальная форма функции

f ( x, y,z )=x y z x y z x y z x y z

есть

f

 

x, y,z

 

 

 

 

 

 

 

 

 

 

 

• Пример 3.

 

 

 

 

 

 

y

.

Найдите минимальную форму логической функции:

fx1 ,x2 ,x3 ,x4 x1x2 x3 x4 x1x2 x3 x4 x1x2 x3 x4

x1x2 x3 x4 x1x2 x3 x4 x1x2 x3 x4 x1x2 x3x4

.

Решение.

Сложность функции равна 7∙4=28.

Функция задана в СДНФ. Заполним для неё карту Карно.

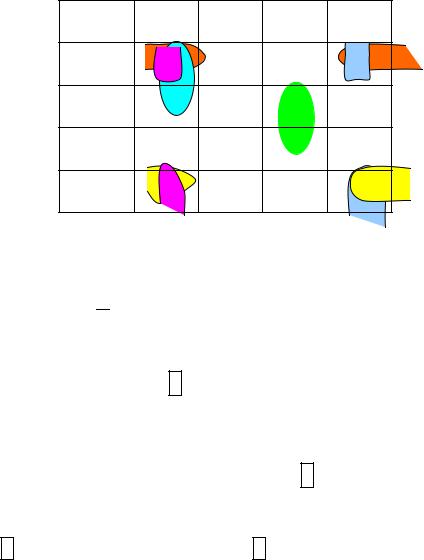
x

x

1

2

x

x

1

2

x

x

1

2

x

x

1

2

x

x

x

x

x

x

x

x

3

4

3

4

3

4

3

4

1

 

 

 

 

1

1

 

 

1

 

 

 

 

 

 

1

 

 

1

 

 

 

 

1

Пары соседних ячеек, заполненных 1-цами, выделены овалами одного цвета.

Соседним клеткам цвета соответствуют 2 логических слагаемых СДНФ

x x

x x

x x x

x

, которые по свойству дистрибутивности объединяются в конъюнкцию

1 2

3 4

1 2 3

4

x x x

. Или соседним клеткам цвета

 

соответствуют фиксированные значения

x x x

, что

1 3 4

 

1 3 4

 

и является результатом объединения.

 

 

 

 

Результат объединения соседних клеток цвета

 

является конъюнкция

x x x

, а

 

 

2 3 4

клеток цвета

 

- x1x2 x4 и клеток цвета

 

- x1x2 x4 .

 

 

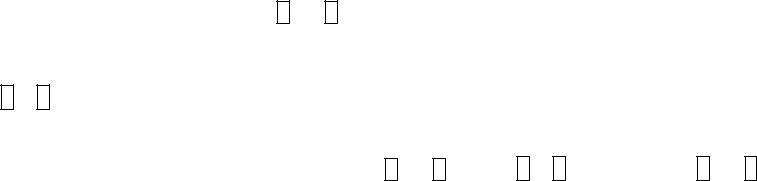
Две пары соседних клеток цвета

 

и

 

 

объединяются в результате чего получается

 

конъюнкция

x x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 4 . Этот же результат мог быть получен объединением 2-х пар соседних

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

клеток

 

и

 

. Таким образом, 4 соседние клетки объединяются в минимальную форму,

 

состоящую из 2-х термов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Результат минимизации – объединение 4-х (

 

и

 

 

или

 

 

и

 

) и 2-х пар (

 

и

 

 

)

соседних клеток – функция

f x

, x

, x

, x

x x

x x x

 

x x x

сложности 8, первые 2

 

1

2

3

4

2 4

1 3 4

 

2 3 4

 

слагаемые которой по свойству дистрибутивности объединяются в скобочную форму:

f x

, x

, x

, x

x

x x

x

x x x

1

2

3

4

2

1

3

4

2

3

4

.

Сложность полученной минимальной формы равна 7.

(Под)тема 3: Функциональная схема бинарной функции

Для построения функциональной схемы используют минимальную форму функции и следующие обозначения логических операций:

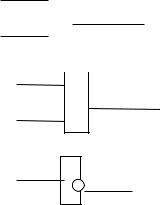
a b

a ba

-

-

a

a

 

 

 

 

 

 

 

 

 

1

 

 

a b

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

&

a b

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

 

 

-

a 1 a

Пример 1. Необходимо построить функциональную схему для функции примера 3 предыдущего параграфа.

Решение.

Минимальная форма логической функции

f x1 ,x2 ,x3 ,x4 x1x2 x3 x4 x1x2 x3 x4 x1x2 x3 x4

x1x2 x3 x4 x1x2 x3 x4 x1x2 x3 x4 x1x2 x3x4 ,

найденная методом карты Карно, -

f x

, x

, x

, x

x

x x

x

1

2

3

4

2

1

3

4

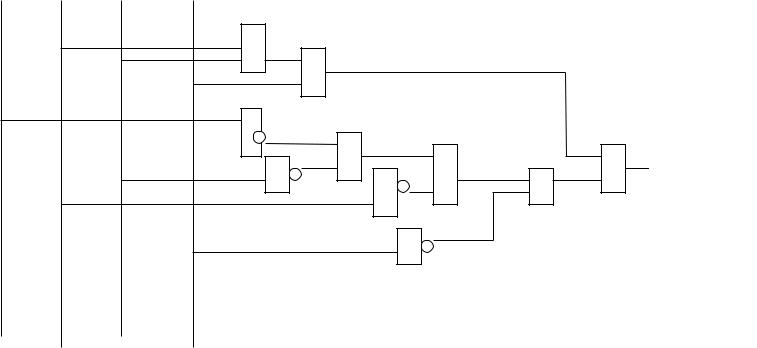
Её функциональная схема –

x x x

2

3

4

.

&

&

1

 

&

1

 

1

 

1

 

 

f(x1,x2,x3,x4)

 

1

&

 

 

 

 

 

 

 

1

 

 

 

X1

 

 

 

x3

 

 

X2

 

x4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(Под)тема 4: Представление булевой функции многочленом Жегалкина

• Многочлен (полином) Жегалкина булевой функции – её представление в следующем виде

 

 

f x1 ,x2 ,...xn a0

a1x1 a2 x2 a3 x3

... an xn

 

 

a

x x

a

x x

 

... a

 

 

x

x

a

x x x ... a

x x

x

 

12

1 2

 

13 1 3

 

 

 

 

n 1 n

123 1 2

3

12K n

1 2

n ,

 

 

 

 

 

n 1 n

 

где коэффициенты

a

, a

 

,a

 

, ...,a

 

 

{ 0,1}

i, j,k

- булевы константы, а

 

i

 

ij

 

 

ijk

 

 

12 K n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-

логическая операция сложения по модулю 2.

• Пример 1. Если функция в формате многочлена Жегалкина имеет вид

f x ,x ,x ,x

1 x x

x x

x x

x

x x

,

1

2

3

4

1

4

1

2

1

3

2

3

4

то, сравнивая её с определением общего вида многочлена Жегалкина, это означает,

что

а

а

а

а

а

а

1

,

 

 

 

0

1

 

4

12

13

234

 

 

 

 

а2 а3 а14

а23 а24 а34 а123 а124

а134

а1234

0 .

• Теорема 1. Любая бинарная функция представима многочленом Жегалкина единственным

образом.

Доказательство.

Так как любая бинарная функция представима СДНФ единственным образом, то

для доказательства единственной представимости функции многочленом Жегалкина

достаточно выразить операции логического сложения

 

,

умножения

 

и отрицания

 

 

 

через операцию сложения по модулю 2

 

и логического умножения

 

. Операция

 

 

 

 

 

 

 

 

является элементом многочлена Жегалкина и не требует доказательства. Выражение

 

операции −

p 1 p

, а − p q p q p q , что и доказывает единственную

 

представимость.

•Методы приведения бинарной функции к форме многочлена Жегалкина:

1.тождественные преобразования,

2.решение системы линейных уравнений относительно неизвестных коэффициентов

а) методом последовательного исключения неизвестных.

б) методом Гаусса.

Соседние файлы в предмете Математическая логика и теория алгоритмов
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности