Федеральное агенство связи

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

“Московский технический университет связи и информатики”

Кафедра “Информатика”

Лабораторная работа 4 по дисциплине “Минимизация логических выражений”

Выполнил студент

Вариант №1

Проверил Сёмин В.Г.

г. Москва, 2020

Содержание

1 Ход выполнения лабораторной работы 3

.1 Задание №1 3

.2 Задание №2 5

Для заданного логического выражения написать каноническую сумму минтермов и нарисовать минимальную логическую схему. (Таблица 4,5,6) 5

5

8

10

10

.3 Задание №3 13

1. Ход выполнения лабораторной работы

1. Задание №1

Написать минимальное выражение для заданной таблицы истинности и нарисовать по нему логическую схему по таблице 1

Таблица 1 –Таблица логической функции

Решение задачи №1

Чтобы решить поставленную задачу, нужно найти МДНФ, поэтому беру в таблице 1 строчки с ответом равному 1

a	b	c	d	F
0	0	0	0	1
0	1	0	1	1
1	0	1	0	1

Таблица 2

Рассматривая таблицу 2 составляю каноническая сумма минтермов. В таблице 2 беру за единицу обычную переменную, а с нулем инверсионное значение данной переменной. Например, в 3 строке, в столбце с переменной «а», я беру «а», а в столбце с «b» я беру « », так как у «b» значение нулевое, поэтому ставлю инверсию.

Основываясь на этом я составляю функцию F.

	d	0	0	1	1
a	b c	0	1	1	0
0	0	1	0	0	0
0	1	0	1	0	0
1	1	0	0	0	0
1	0	0	0	0	1

Таблица 3-Минимизация методом карт Карно

Данную функцию минимизировать нельзя, значит выражение F является минимальным

Основываясь на функции F составляю логическую схему. Составление логической схемы начинаю сначала, а именно с инверсий и умножений, а в дальнейшем все складываю

Рисунок 1 – Логическая схема

1. Задание №2

Для заданного логического выражения написать каноническую сумму минтермов и нарисовать минимальную логическую схему. (Таблица 4,5,6)

Таблица 4 – Начальные значения

Решение задачи №2

Чтобы решить поставленную задачу, нужно найти МДНФ, поэтому в таблице 3 беру строчки с ответом равному + и составляю таблицу истинности, где + это функция F с ответом равному единице, а значение над + перевожу в двоичную систему исчисления.

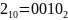
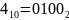
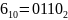
a	b	c	d	F
0	0	0	0	1
0	0	0	1	0
0	0	1	0	1
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

Таблица 5-Таблица истинности для всех значений функции

a	b	c	d	F
0	0	0	0	1
0	0	1	0	1
0	1	0	0	1
0	1	1	0	1
1	0	0	0	1

Таблица 6

Аналогичным способом, как в предыдущем задании, составляю функцию F

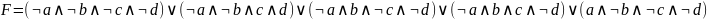
	d	0	0	1	1
a	b c	0	1	1	0
0	0	1	1	0	0
0	1	1	1	0	0
1	1	0	0	0	0
1	0	1	0	0	0

Таблица 7-Минимизация методом карт Карно

Рассматриваю оранжевые ячейки. По оси a и b, b не меняется и b =0 => b По оси c и d ничего не меняется, и c, и d равны 0 => => итоговое выражение

Рассматриваю синие ячейки. По оси a и b, a не меняется и a =0 => a По оси c и d, d не меняется и d =0 => d => итоговое выражение

МДНФ имеет вид:

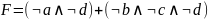
Основываясь на функции F составляю логическую схему. Составление логической схемы начинаю сначала, а именно с инверсий и умножений, а в дальнейшем все складываю

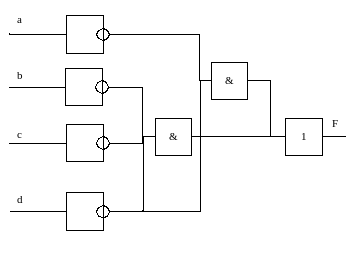
Рисунок 2 – Логическая схема

Таблица 4 – Начальные значения

Составляю таблицу истинности:

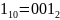
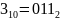
b	c	d	F
0	0	1	1
1	1	0	1

Таблица 5

a	b	d	F
0	1	1	1

Таблица 6

a	b	F
1	1	1

Таблица 7

Общая таблица истинности:

a	b	c	d	F
0	0	0	0	0
0	0	0	1	1
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	1
0	1	1	0	1
0	1	1	1	0
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

Таблица 5-Таблица истинности для всех значений функции

Аналогичным способом, как в предыдущем задании, составляю функцию F

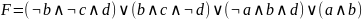
	d	0	0	1	1
a	b c	0	1	1	0
0	0	0	0	0	1
0	1	0	1	0	1
1	1	1	1	1	1
1	0	0	0	0	1

Таблица 7-Минимизация методом карт Карно

Рассматриваю оранжевые ячейки. По оси a и b, все значения меняются => ничего не пишу. По оси c и d ничего не меняется, с=0 d =1 =>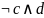 => итоговое выражение

Рассматриваю синие ячейки. По оси a и b, ничего не меняется и a, и b =1 => 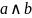По оси c и d, все меняется => 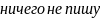=> итоговое выражение

Рассматриваю красные ячейки. По оси a и b, b не меняется и равно 1 => 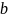. По оси c и d, ничего не меняется c=1 d=0 => => итоговое выражение

МДНФ имеет вид:

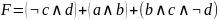
Основываясь на функции F составляю логическую схему. Составление логической схемы начинаю сначала, а именно с инверсий и умножений, а в дальнейшем все складываю

Рисунок 3 – Логическая схема

Таблица 8 – Начальные значения

Составляю таблицу истинности:

a	b	c	F
0	0	0	1
0	1	1	1
1	1	0	1

Таблица 9

a	c	d	F
0	1	0	1
1	0	1	1

Таблица 10

Общая таблица истинности:

a	b	c	d	F
0	0	0	0	1
0	0	0	1	1
0	0	1	0	1
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0
1	0	0	1	1
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

Аналогичным способом, как в предыдущем задании, составляю функцию F

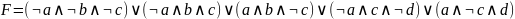
	d	0	0	1	1
a	b c	0	1	1	0
0	0	1	1	0	1
0	1	0	1	1	0
1	1	1	0	0	1
1	0	0	0	0	1

Таблица 7-Минимизация методом карт Карно

Рассматриваю желтые ячейки. По оси a и b, a не меняется и равно 1 => a. По оси c и d ничего не меняется, с=0 d =1 => => итоговое выражение

Рассматриваю синие ячейки. По оси a и b, ничего не меняется a=0, b =1 => 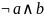По оси c и d, c не меняется c=1 => => итоговое выражение

Рассматриваю красные ячейки. По оси a и b, a не меняется и равно 0 => 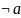. По оси c и d, ничего не меняется c=1 d=0 => => итоговое выражение

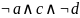
Рассматриваю зеленые ячейки. По оси a и b, ничего не меняется a=1, b =1 => По оси c и d, c не меняется c=0 => => итоговое выражение

Рассматриваю фиолетовые ячейки. По оси a и b, ничего не меняется a=0, b =0 => 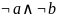По оси c и d, c не меняется c=0 => => итоговое выражение

МДНФ имеет вид:

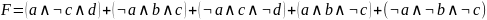
Основываясь на функции F составляю логическую схему. Составление логической схемы начинаю сначала, а именно с инверсий и умножений, а в дальнейшем все складываю

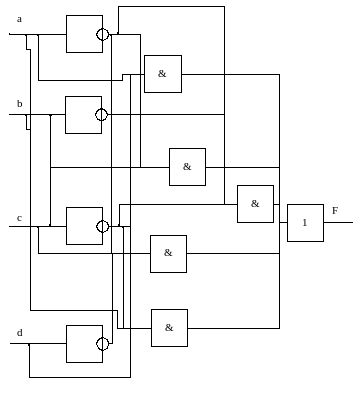
Рисунок 3 – Логическая схема