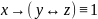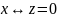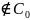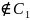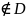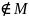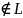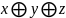КР 2 вар 3
.docx

Задание №1
|
|
|
|
|
|
1 |
0 |
0 |
|
|
|
1 |
0 |
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
Для синего
:
В столбце с х и у беру только те
ячейки, которые не изменяются, то есть
беру
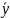 В столбце с z и t
беру
В столбце с z и t
беру
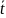 =>
Итоговое выражение
=>
Итоговое выражение
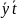
Для
оранжевого: беру целиком

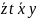
МДНФ:
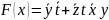
Скобочная форма: в скобочной форме представить невозможно.
Логическая схема:
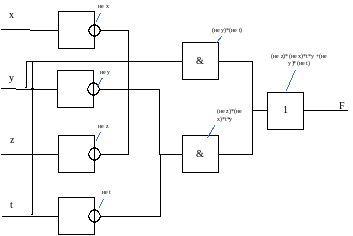
x |
y |
z |
t |
Треугольник |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
t |
0 |
0 |
1 |
0 |
00110110001000 |
|
0 |
0 |
1 |
1 |
0101101001100 |
|
0 |
1 |
0 |
0 |
|
y |
0 |
1 |
0 |
1 |
00110011111 |
|
0 |
1 |
1 |
0 |
0101010000 |
|
0 |
1 |
1 |
1 |
111111000 |
yzt |
1 |
0 |
0 |
0 |
00000100 |
|
1 |
0 |
0 |
1 |
0000110 |
|
1 |
0 |
1 |
0 |
000101 |
|
1 |
0 |
1 |
1 |
00111 |
|
1 |
1 |
0 |
0 |
0100 |
|
1 |
1 |
0 |
1 |
110 |
xyt |
1 |
1 |
1 |
0 |
01 |
|
1 |
1 |
1 |
1 |
1 |
xyzt |
Получаем:
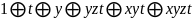
Задание №2
x |
y |
z |
(x∨y)⊕z≡1 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
|
Система имеет 2 решения: x=0, y=0, z=1 и x=0,y=1,z=0
Задание №3
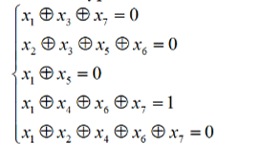
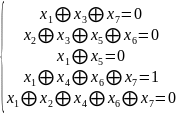
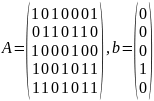

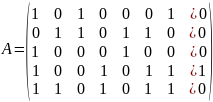
(5) –((2)+(1))
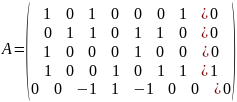
Меняю 3 и 5 строку местами
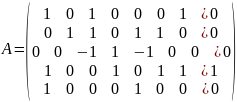
(4)+ (5)*(-1)
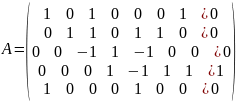
(5)+(1)*(-1)
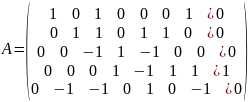
(5)+(2)
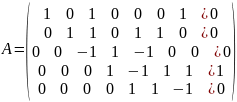
Делим каждую строку на ведущий элемент
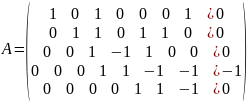
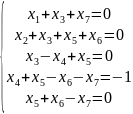
Базисные
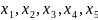 Свободные
Свободные
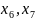
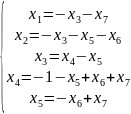
При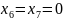
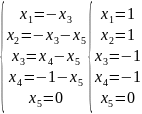
При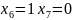
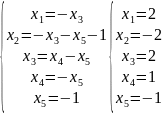
При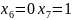
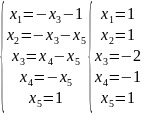

Где
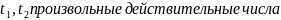
Задание №4
|
|
|
|
|
|
0 |
- |
+ |
+ |
- |
- |
1 |
+ |
- |
+ |
- |
- |
x |
+ |
+ |
+ |
+ |
+ |
x<-y |
+ |
- |
+ |
+ |
+ |
|
- |
- |
- |
+ |
- |
Проверим критерии для x<-y
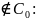 F(0,0)=1 => +
F(0,0)=1 => +
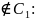 F(1,1)=1=> -
F(1,1)=1=> -
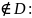
x |
y |
x<-y |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
Не самодвойственна=>+
Строю диаграмму хосе
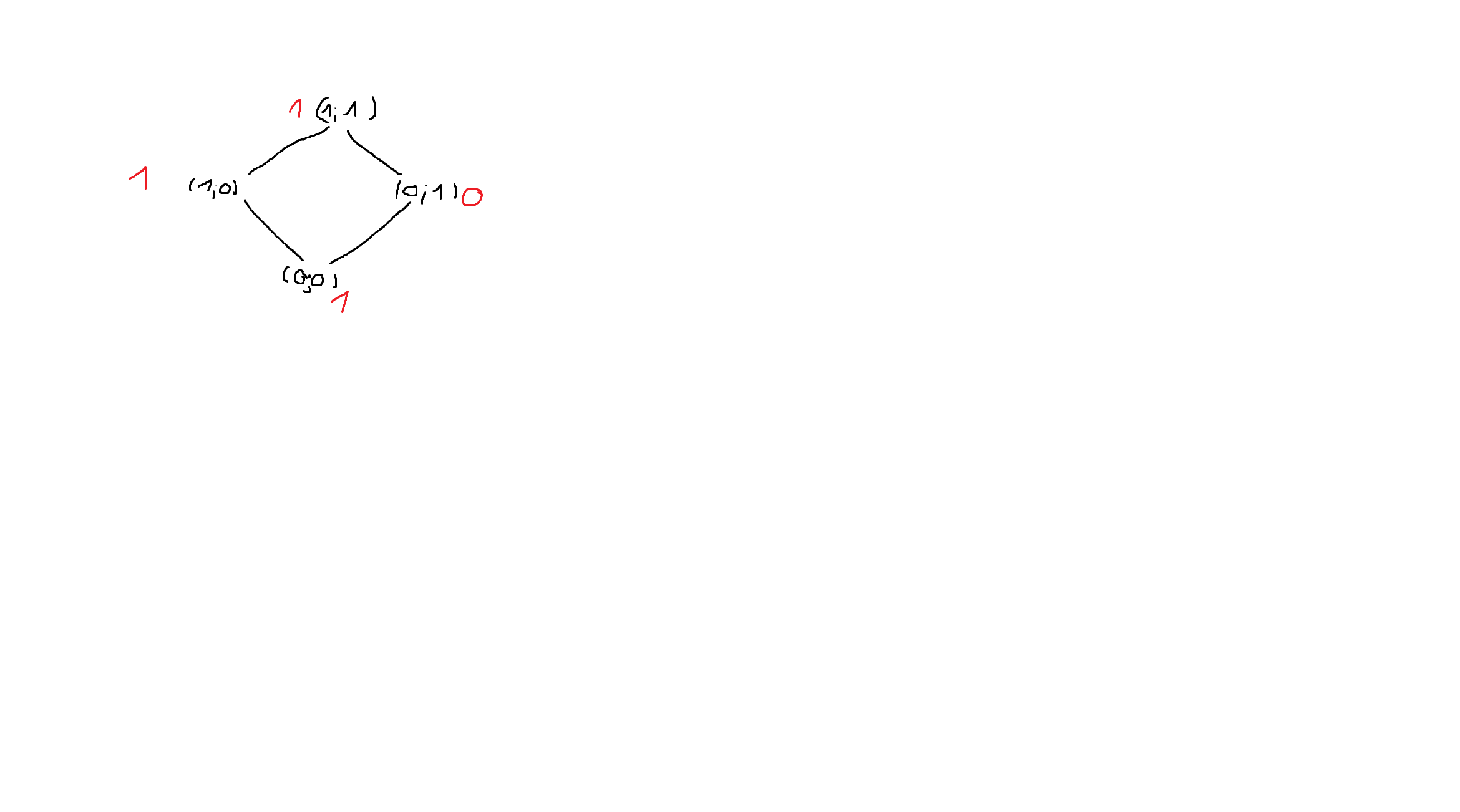
Функция не монотонна, так как по пути 0,0 ->0,1 ->1,1 функция меняет свое значение с 1 на 0 и с 0 на 1=>+
x |
y |
Треугольник |
|
0 |
0 |
11011 |
1 |
0 |
1 |
110 |
y |
1 |
0 |
01 |
|
1 |
1 |
1 |
xy |
Получаем:
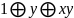 =>не линейная функция=>+
=>не линейная функция=>+
Проверим критерии для
F(0,0,0)=0 => -
F(1,1,1)=1=> -
x |
y |
z |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Cамодвойственна=>-
Строю диаграмму хосе
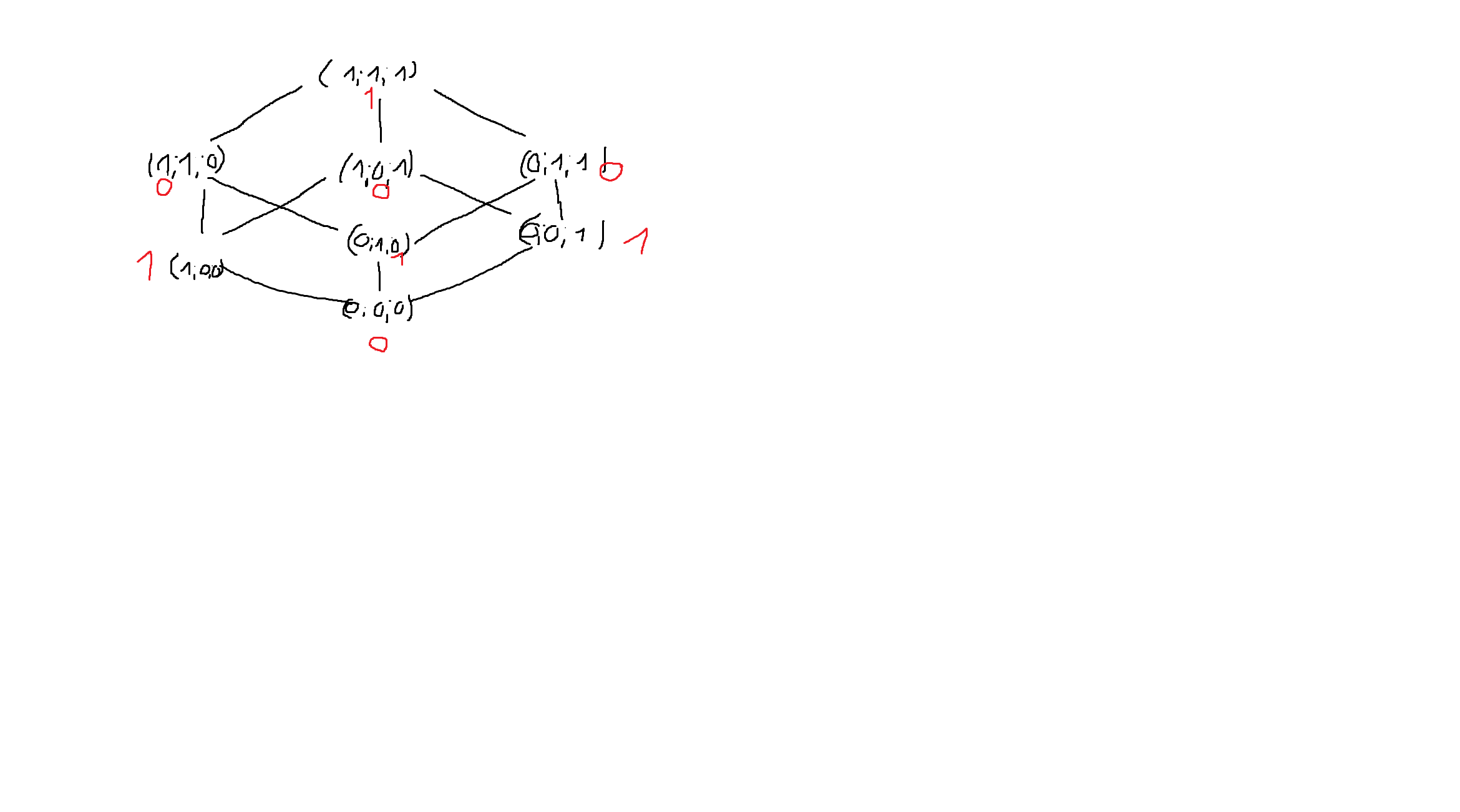
Функция не монотонна, так как по пути функция меняет свое значение с 1 на 0 и с 0 на 1=>+
x |
y |
z |
|
|
0 |
0 |
0 |
001101001 |
|
0 |
0 |
1 |
1011101 |
z |
0 |
1 |
0 |
110011 |
y |
0 |
1 |
1 |
01010 |
|
1 |
0 |
0 |
1111 |
x |
1 |
0 |
1 |
000 |
|
1 |
1 |
0 |
00 |
|
1 |
1 |
1 |
0 |
|
Получаем: =>линейная функция=>-
Заполнив всю таблицу, получаются следующие базисы {x},{0,<-}


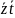
 1
1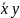
 0
0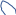 0
0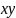
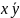
 1
1 11010010010100000
11010010010100000 111011011110000
111011011110000 111011101010
111011101010