Лекция 13. Аутентификация ПО
Цель аутентификации сообщений:
Обнаружить модификацию (изменение) сообщения M (обеспечить его
целостность).
Техника аутентификации («Основы криптографии») |
|
|||||
- симметричная ( E |
f (M ,K) (M ,E ) ), где E |
- аутентификатор, K |
- ключ |
|||
аутентификации; S |
~ |
~ |
S |
S |
|
|
~ ~ |
~ |
? ~ |
|
|
||
верификация : (M,ES) ES |
f (M |
,K),ES |
ES) |
|
|
|
- несимметричная на основе РША ( S hd modn, h h(M ) (M ,S) , гдеh(...) -
бесключевая хэш функция, d |
- секретный ключ РША, |
n - модуль РША, S - |
||||
цифровая подпись (ЦП); |
|
|
|
|
||
~ |
~ |
~ |
~ |
~ |
~ ~ ? ~ |
-открытый ключ РША. |
верификация: (M |
,S ) h h(M ),S emodn h,h h) , где e |
|||||
Особенность аутентификации в стеганографии: |
|
|||||
Аутентификатор ES или ЦП |
S |
должны быть погружены в ПО, а не |
||||
присоединены к нему в виде attachment (как обычно)! |
|
|||||
1
Два основных вида аутентификации в СГС:
1.Точная аутентификация (искажение даже одного бита в ПО должно обнаруживаться)
2.Селективная аутентификация (некоторые виды искажения ПО должны обнаруживаться, а другие искажения (например, добавление небольшого шума, преобразование формата и т.п.) не должны обнаруживаться).
«Парадокс» аутентификации в СГС:
при погружении аутентификатора как ЦВЗ в ПО оно неизбежно искажается, а, с другой стороны, искажение ПО приводит к невозможности его аутентификации…
Применение аутентификации в СГС:
-для медицинских изображений,
-в криминалистике (отпечатки пальцев и фотографии),
-в камерах видеонаблюдения,
-для обеспечения подлинности речевых сообщений,
-для обеспечения подлинности «бумажных подписей».
Замечание. Хотя ПО после правильного извлечения ЦВЗ может быть в точности восстановлено, но и после погружения ЦВЗ (до его извлечения) ПО не должно значительно искажаться.
2
Основная техника аутентификации в СГС:
1.Использование полей, которые не нуждаются в аутентификации (служебные поля изображений, паузы речи и т.п.)
2.Модульное погружение.
3.Обратимое погружение:
3.1.Обратимое погружение со сжатием.
3.2.Обратимое погружение с использованным естественной избыточности ПО.
Ввиду тривиальности 1-го метода, рассмотрим далее методы 2 и 3.
3
2. Модульное погружение ЦВЗ
Сw С(n) ( 1)b (n), n 1,2,..., N, (n) iid, (n) { 1}, b {0,1} {ES или S}. |
||||
|
|
|
|
|
b |
(n) , однако, если Cw (n) |
или Cw (n) L , где |
||
C(n) Cw (n) ( 1) |
|
|||
L - число уровней квантования, то возникают необратимые искажения. |
|||||||
Выход: использовать для вложения и извлечения модульные операции: |
|||||||
Сw С(n) |
|
|
b |
|
сложение по mod L, |
|
|
( 1) |
(n) |
|
(1) |
||||
~ |
|
|
|
b |
|
вычитаниепо mod L |
|
|
|
|
|
|
|||
C(n) Cw (n) ( 1) |
(n) |
|
|
||||
~ |
|
|
|
|
|
~ |
|
С(n) С(n), если |
b b(декодирование выполнено верно) |
||||||
. Обобщение техники УШПС на модульное погружение |
|
||||||
Сw С(n) ( ( 1)b x) (n), n 1,2,..., N, |
(2) |
||||||
|
|
|
N |
|
|
|
|
где x |
|
|
C(v) (v), […] – означает выбор ближайшего уровня квантования |
||||
|
N |
||||||
|
|
v 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Особенность модульного погружения:
Декодирование при модульном погружении (1) приводит к значительно
~
большим ошибкам p P{b b}, чем при обычном (линейном) погружении.
4
Декодеры (детекторы) ЦВЗ при модульном погружении
1.Центрированный корреляционный детектор
|
|
N |
|
~ |
|
0,если CD 0 |
|
(3) |
|
|
|
|||||
CD |
(Cw (n) Co) (n) b |
|
если CD 0 |
, |
|
|
|
|
|
|||||||
|
n 1 |
N |
|
|
1, |
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
где Со |
|
|
|
Cw (n) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
N n 1 |
|
|
|
|
|
|
|
|
|
|
||
2. Оптимальный модульный |
|
|
|
|
|
|
|
|
|
|||||||
детектор |
|
|
|
|
|
|
|
~ |
0,если MD 0 |
|
||||||
|
|
N |
|
((Cw (n) (n)) Co ) |
2 |
|
N |
|
|
2 |
(4) |
|||||
MD |
|
((Cw (n) (n)) Co ) |
|
b |
|
если MD 0 |
||||||||||
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
1, |
|
||||
. Разностный детектор (базируется на большой корреляции соседних отсчетов ПС):
N 1 |
|
|
~ |
0,если DD |
0 |
(5) |
|
|||
DD |
(Cw (n 1) Cw (n))( (n 1) (n)) |
b |
|
|
|
0 |
|
|||
n 0 |
|
|
|
|
1,если DD |
|
|
|||
4. Преобразование фильтром Винера: |
|
|
|
|
|
|
|
|||
~ |
~ |
~ |
|
|
|
(6) |
|
|
|
|
Сw Сw (n) |
С(n), |
где С(n) wiener(Cw (n)) |
|
|
|
|
|
|
||
Для изображенийCw (n) Cw (n1,n2) (см. Matlab): |
|
|
|
|
|
|||||
~ |
2 2 |
(Cw (n1,n2 ) ), |
|
|
|
|
|
|
|
|
C(n) |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
где |
(I) 1 (n ,n ) I Cw (n1,n2 ), 2 |
(I) 1 (n ,n ) I Cw2 |
(n1,n2 ) 2 , 2 2 |
, |
||||||
|
|
1 |
2 |
|
1 |
2 |
|
|
|
5 |
-I задаваемая область вокруг каждого пикселя. |
|
|
|
|
||||||
|
|
|
|
|
||||||
Расчеты вероятностей ошибок для различных методов погружения и извлечения ЦВЗ
Для всех элементов (в силу ЦПТ) справедливо выражение:
p Q( |
|
E( ) |
|
) |
(7) |
|
|
|
|||
' |
|||||
|
|
Var |
|
||
Однако, теоретический расчетE{ },Var{ }для различных (см. 3÷6)
оказывается весьма сложным и зависящим от распределения вероятностей ПО [
|
p |
|
p |
|
|
|
|
1 |
0.45 |
6 |
0.487 |
|
|
|
|
2 |
0.24 |
10 |
0.439 |
|
|
|
|
3 |
0.053 |
20 |
0.352 |
|
|
|
|
4 |
0.122 |
30 |
0.301 |
|
|
|
|
5 |
0.328 |
|
|
|
|
|
|
p |
|
Вероятности ошибокдля корреляционного детектора, типичного изображения и |
|
N 1000 |
|
Замечание. Для модульного погружения вероятность |
p не является |
ошибки |
|
монотонно-убывающей функцией «амплитуда сигнала» |
|
6
Расчет вероятностей ошибок методом моделирования для различных методо погружения и извлечения ЦВЗ с предобработкой фильтром Винера
N |
|
|
Изображения |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
||
|
|
|
|
|
|
|
|
CD |
|
DD |
CD |
|
DD |
|
|
|
|
|
|
|
50 |
0.0593 |
|
0.062 |
0.0105 |
|
0.0077 |
|
|
|
|
|
|
|
100 |
0.02 |
|
0.020 |
0.0044 |
|
0.0044 |
|
|
|
|
|
|
|
200 |
0.0035 |
|
0.0046 |
0.0015 |
|
0.0019 |
|
|
|
|
|
|
|
500 |
0 |
|
0 |
0.0007 |
|
0.0007 |
|
|
|
|
|
|
|
1000 |
0 |
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
1- изображение 1
2 - изображение 2
CD – корреляционный детектор DD – разностный детектор N-длина ШПС
Вывод: Для наилучших методов модульного погружения и извлечения, в типовые изображения с 256 градациями серого, можно погрузить около 100-300 бит аутентификатора или ЦП.
Замечания. Изображения после модульного погружения остаются визуально распознаваемыми, однако возникают искажения на черном и белом полях,
называемых «соль» и «перец». |
7 |
|
3. Обратимое погружение общего вида.
3.1. Обратимое погружение со сжатием
Факт. Невозможно выполнить обратимое погружение, если ПО не имеет избыточности.
Замечание. Непосредственное сжатие ПО (изображения или звука) приводит к полному их искажению для восприятия человеком.
Поэтому необходимо использовать более изощренные методы погружения со сжатием без потерь, которое не искажает заметно ПО сразу после погружения аутентификаторов.
8
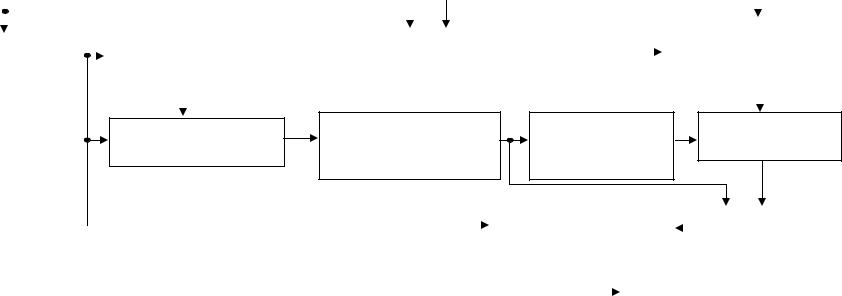
Алгоритм погружения ЦВЗ |
|
|
Ключ |
M |
|||||||||
|
C n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
аутентификации |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разбиение ПО |
|
|
Формирование |
|
Формирование |
|
|
Аутентификатор (ПО) |
||||
|
|
|
модифицированной |
|
|
|
и дополнительная |
||||||
|
на группы G |
|
|
|
ES (S) |
|
|
||||||
|
|
|
|
|
|
||||||||
|
|
|
группы G’ |
|
|
|
информация |
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Классификация |
Формирование |
Сжатие RS- |
Вложение ЦВЗ |
|
двоичного вектора |
вектора без |
(RSM – вектор) |
||
групп (R,S,U) |
||||
RS |
потерь |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразование |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Сравнение RS и |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
групп |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пояснения: |
|
|
|
|
|
|
|
|
RSM - векторов |
|
||||||||
|
|
|
|
|
(«Перескок уровней») |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||||||||
1. Разбиение C(n) на группы: G1,G2 ,...,GN / K |
|
|
|
|
|
|
|
|||||||||||
|
|
Cw (n) |
|
|
||||||||||||||
|
|
|
|
|||||||||||||||
2. Формирование модифицированной группы G' (C1' ,C2' ...Ck' ), где Сi' F(Ci ), G (C1,...,Ck ) |
||||||||||||||||||
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F(C) задает перестановку уровней квантования: |
|
|
|
|
|
|||||||||||||
Пример. 0 1,2 3,...,254 255(НЗБ);0 2,1 3,4 6,5 8,...и т.д. |
|
|
||||||||||||||||
A |
1 |
|
|
C F(C) |
|
, где I -множество уровней квантования, |
A - амплитуда |
|||||||||||
|
|
|||||||||||||||||
|
||||||||||||||||||
|
L C I |
|
|
|
|
перескоков. Свойство F(C) : F(F(C)) C |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
3. Классификация групп: |
|
|
|
|
|
|||||||||||||
|
|
|
|
G R, если f (F(G)) f (G) ( регулярные группы) |
|
|
|
|
|
|||||||||
|
|
|
|
G S, если f (F(G)) f (G) (сингулярные группы) |
|
|
|
|
|
|||||||||
|
|
|
|
G U, если f (F(G)) f (G) (неиспользуемые группы) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
||||||
|
|
|
|
где f (C) f (C1...CK ) |
Ci 1 Ci |
(дискриминантная функция) |
(8) 9 |
|
||||||||||
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
4. |
Формирование двоичногоRS-вектора: R 1, S 0,U Ø |
. |
|
||||||||||||
5. |
Сжатие RS-вектора без потерь: RS' Ф(RS), |
|
RS |
|
LRS , RS' |
|
LRS' , LRS ' LRS , |
||||||||
|
|
||||||||||||||
|
|
||||||||||||||
Ф 1(..) :Ф 1(RS' ) RS |
|
|
|
|
|
|
|
|
|
|
|||||
6.Вложение ЦВЗ: RSM (RS',C), |
|
C |
|
L |
L |
, где С (M,E (S)) |
|||||||||
|
|
||||||||||||||
|
|
|
|
|
|
RS |
RS' |
|
|
|
|
|
S |
|
|
7. |
Сравнение векторов RSM и RS: |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
xi |
xi' i 1, xi xi' i 0, где |
|
|
|
|
|
|
|
|
|
|
||||
xi |
i - ый символ вектора RS, xi' i - ый символ вектора RS'. |
|
|||||||||||||
8. Преобразование групп:
Gi' F(Gi ),i 1,2,..., N / k, если i 1, Gi' Gi , если i 0 или Gi 0
Свойство функции перескока:
F(R) S, F(S) R, F(U ) U
Замечание.
Можно выбрать любой алгоритм сжатия без потерь, но наиболее предпочтительным является использование адаптивных арифметических кодов . [ ]
10