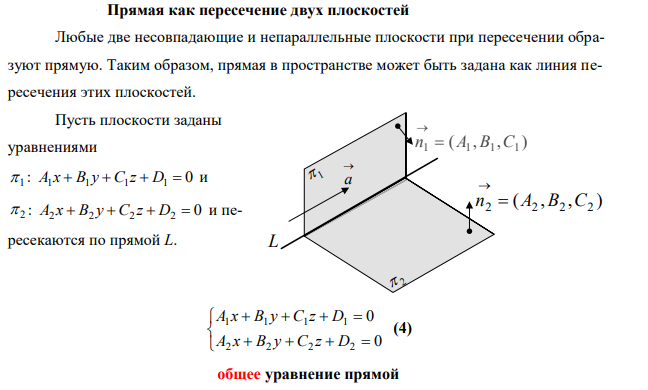
1 9. Прямая в пространстве. Канонические и параметрические уравнения прямой. Уравнение прямой, проходящей через две различные точки. Прямая как линия пересечения плоскостей.

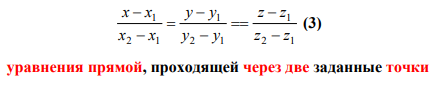
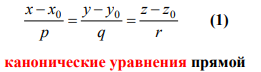
20. Взаимное расположение двух прямых. Нахождение угла между прямыми. Расстояние между параллельными и скрещивающимися прямыми.

Расстояние между скрещивающимися прямыми равно отношению модуля смешанного произведения векторов (r₂ − r₁), s₁ и s₂ к модулю векторного произведения векторов s₁ и s₂. Геометрический смысл формулы: расстояние — это длина высоты параллелепипеда (построенного на векторах (r₂ − r₁), s₁ и s₂), опущенной на основание в виде параллелограмма (построенного на векторах s₁ и s₂), равная отношению объёма параллелепипеда к площади параллелограмма

Р асстояние между параллельными прямыми равно отношению модуля векторного произведения векторов (r₂ − r₁) и s₁ к длине вектора s₁. Геометрический смысл формулы: расстояние — это длина высоты параллелограмма (построенного на векторах (r₂ − r₁) и s₁), опущенной на основание параллелограмма в виде вектора (s₁), равная отношению площади параллелограмма к длине основания

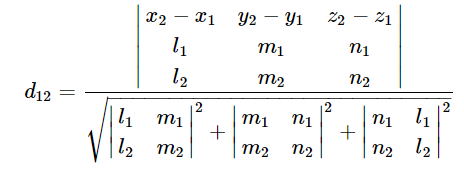
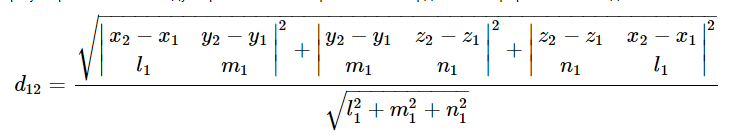Скрещивающиеся прямые: Параллельные прямые:

21. Прямая и плоскость в пространстве, их взаимное расположение. Расстояние от точки до плоскости. Нахождение угла между прямой и плоскостью.

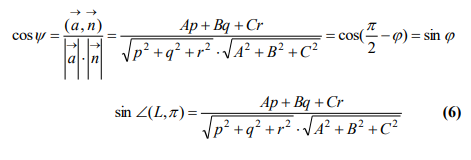
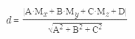Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(M_x, M_y, M_z) до плоскости можно найти, используя следующую формулу:

22. Пересечение прямой и плоскости, нахождение проекций точек на прямую и плоскость и симметричных точек. Нахождение расстояний: от точки до плоскости, от точки до прямой, между плоскостями.

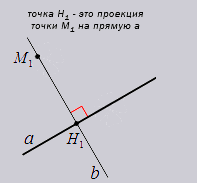На плоскости, чтобы построить проекцию точки М₁ на прямую a нужно провести прямую b, которая проходит через точку М₁ и перпендикулярна прямой a. Тогда точка пересечения прямых a и b является проекцией точки М₁ на прямую a.

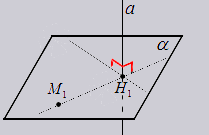В трехмерном пространстве проекцией точки М₁ на прямую a является точка пересечения прямой a и плоскости  , проходящей через точку М₁ перпендикулярно к прямой a.

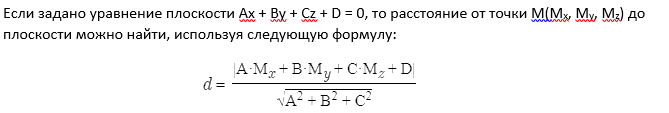
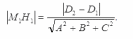
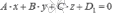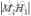В частности, если в прямоугольной системе координат Oxyz плоскости   соответствует общее уравнение плоскости  , а плоскости   - общее уравнение плоскости вида  , то расстояние   между параллельными плоскостями   и   вычисляется по формуле:

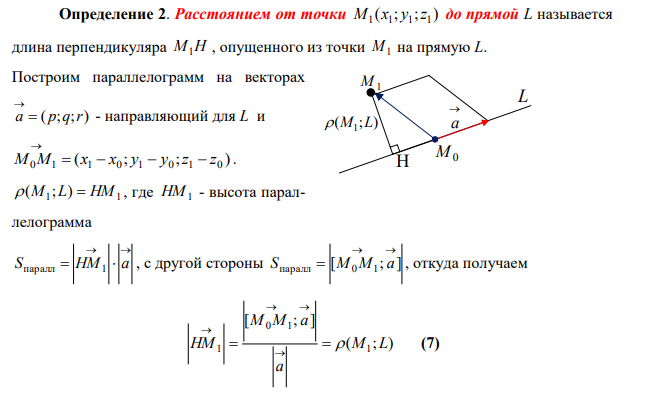
23. Кривые второго порядка на плоскости. Геометрические определения эллипса, гиперболы и параболы. Их канонические уравнения. Построение графиков по заданным каноническим уравнениям. Фокусы, эксцентриситет, асимптоты и директрисы эллипса, гиперболы и параболы. Приведение уравнений кривых второго порядка к каноническому виду, определение типа кривой.

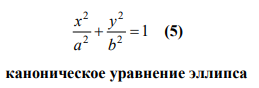
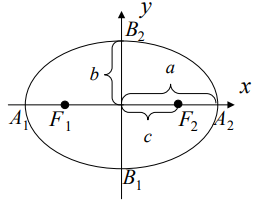
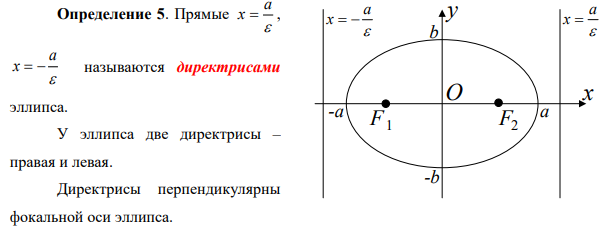
Теорема 1. Если r – расстояние от произвольной точки эллипса до какого-либо фокуса, а d – расстояние от этой же точки до ближайшей к фокусу директрисы, то отношение d r есть постоянная величина, равная эксцентриситету эллипса

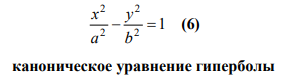
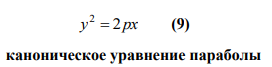
2 4. Поверхности второго порядка в пространстве. Канонические уравнения и графики: эллипсоида, однополостного и двуполостного гиперболоидов, конуса, эллиптического и гиперболического параболоидов, цилиндров (эллиптического, гиперболического и параболического).

25. Приведение уравнений поверхностей второго порядка к каноническому виду, определение типа поверхностей, исследования поверхности с помощью сечения плоскостями. Нахождение точек пересечения поверхности и прямой.

Лекция 13, ее упражнения

26. Определение комплексных чисел в алгебраической форме. Действительная и мнимая части комплексного числа, изображение комплексных чисел на комплексной плоскости. Сопряжение комплексных чисел. Алгебраические операции с комплексными числами: сложение, умножение, деление комплексных чисел и их свойства. Комплексное сопряжение суммы, произведения, отношения двух комплексных чисел.

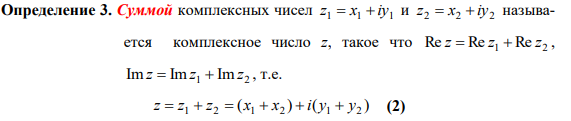
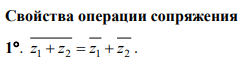
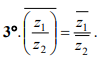
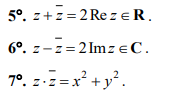
Всякое комплексное число z  x  iy можно представить на плоскости Oxy точкой с координатами (x; y). Поскольку x  Re z , а y  Imz , то ось Ox принято называть действительной осью, а ось Oy – мнимой осью. Плоскость Oxy называется комплексной плоскостью.

27. Тригонометрическая форма записи комплексного числа. Модуль и главное значение аргумента комплексного числа. Формула Эйлера. Показательная (экспоненциальная) форма записи комплексного числа. Действия с комплексными числами в тригонометрической и показательной формах.

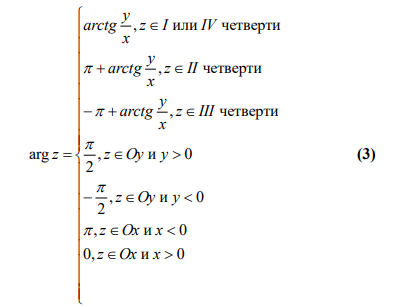
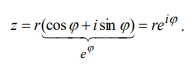
Показательная форма:

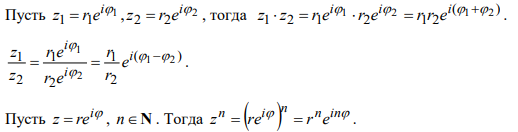
2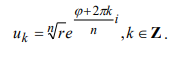 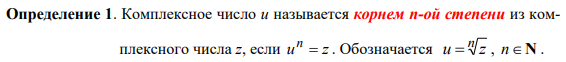8. Возведение в целую степень и извлечение корня натуральной степени из комплексного числа. Формула Муавра.

29. Определение многочлена. Сложение, умножение на число и перемножение многочленов. Алгоритм деления многочлена на многочлен, целая часть, дробная часть и остаток от деления. Теорема Безу. Корни многочлена и их кратность.

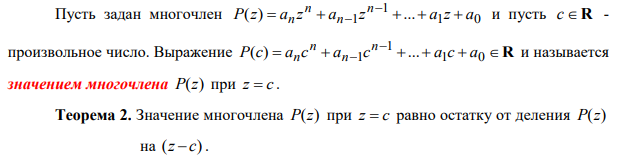
3 0. Основная теорема алгебры многочленов. Разложение многочленов на множители. Многочлены с действительными коэффициентами, их разложение линейные и квадратичные множители.