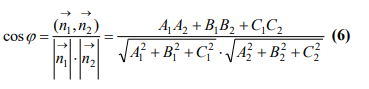7 . Ранг матрицы. Элементарные преобразования матриц. Сохранение ранга матриц при элементарных преобразованиях. Способы нахождения ранга. Базисный минор. Теорема о базисном миноре.

Рангом матрицы A называется наибольший порядок ее ненулевого минора. Ранг матрицы A, как правило, обозначают r(A), rang(A). Для любой матрицы A размера mn верно утверждение 0  rang(A)  min(m,n).

Строки и столбцы матрицы A, которые содержат элементы базисного минора, называются базисными. Базисные строки(столбцы) матрицы линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).

Р анг матрицы можно вычислить методом окаймляющих миноров

И приведением ее к ступенчатому виду (число ненулевых строк равно рангу матрицы)

8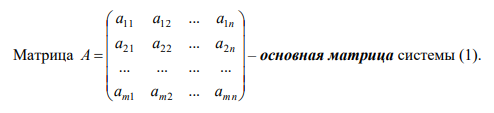 . Основные понятия теории систем линейных алгебраических уравнений: частное решение, общее решение, матрица системы и расширенная матрица системы. Запись линейной системы уравнений в матричном виде.

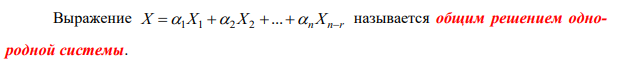
Общее решение с наличием свободных переменных, которые могут принимать любое значение. Частное решение – это численное решение, произведенное от свободного с помощью придания свободным переменным произвольного значения

9. Системы линейных алгебраических уравнений: однородные и неоднородные, совместные и несовместные, определенные и неопределенные. Эквивалентные системы. Элементарные преобразования линейных систем (их матриц). Метод Гаусса решения линейных систем, свободные и базисные неизвестные.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы.

Е сли система линейных уравнений (1) получена из линейной системы (2) элементарными преобразованиями, то системы эквивалентны (то есть множества их решений совпадают).

Те переменные, коэффициенты при которых попали в состав базисного минора, объявляем базисными переменными, остальные – свободными переменными.

С войства однородной системы:

1 0. Фундаментальная система решений однородной системы. Критерий совместности линейной алгебраической системы (теорема Кронекера-Капелли). Условие существования ненулевого решения у однородной системы. Теорема о структуре общего решения совместной неоднородной системы.

О днородная система (6.1) имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных. В частности, однородная система, в которой число уравнений равно числу неизвестных, обладает ненулевым решением тогда и только тогда, когда ее определитель равен нулю.

11. Вектор как направленный отрезок. Линейные операции над векторами: сложение векторов и умножение вектора на число. Свойства линейных операций.

Отрезок называется направленным, если принят во внимание порядок, в котором заданы его концы.

В ектором (или свободным вектором) называется класс всех равных между собой направленных отрезков Класс всех нулевых направленных отрезков называется нулевым вектором

В екторы называются коллинеарными, если существует прямая, которой они параллельны.

В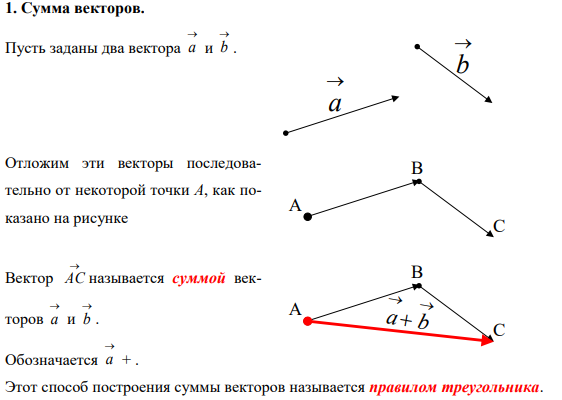 екторы называются компланарными, если существует плоскость, которой они параллельны.

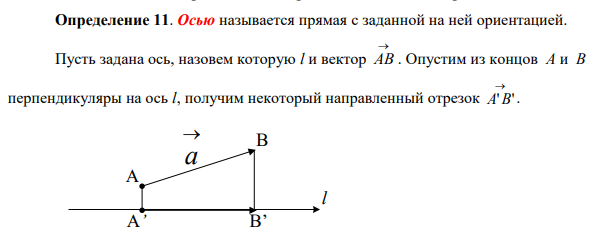
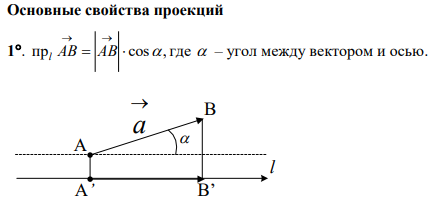
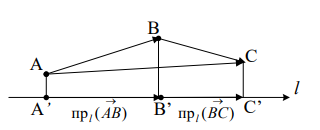
1 2. Проекция вектора на ось. Свойства проекций. Понятие базиса. Декартовы координаты вектора. Канонические базисы 𝑖 ⃗ , 𝑗 ⃗ на плоскости и 𝑖 ⃗ , 𝑗 ⃗ , 𝑘⃗ в пространстве. Деление отрезка в заданном отношении. Условие коллинеарности двух векторов.

П ару векторов называют ортонормированным базисом на плоскости. Тогда разложение вектора a по векторам

Т ройку векторов называют ортонормированным базисом в пространстве. Тогда

разложение вектора а по векторам I, j, k.

13. Компланарные и некомпланарные тройки векторов. Определения правой и левой троек векторов.

Тройка векторов считается компланарной, если их векторное произведение равно 0.

14. Скалярное произведение векторов, его свойства и координатная форма. Вычисление скалярного произведения, нахождение с его помощью длин вектора, угла между векторами и проекции вектора на вектор. Условие ортогональности векторов.

С 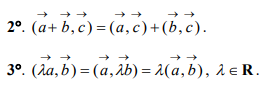войства скалярного произведения:

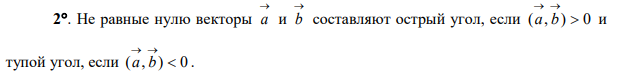
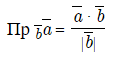
Нахождение проекции вектора а

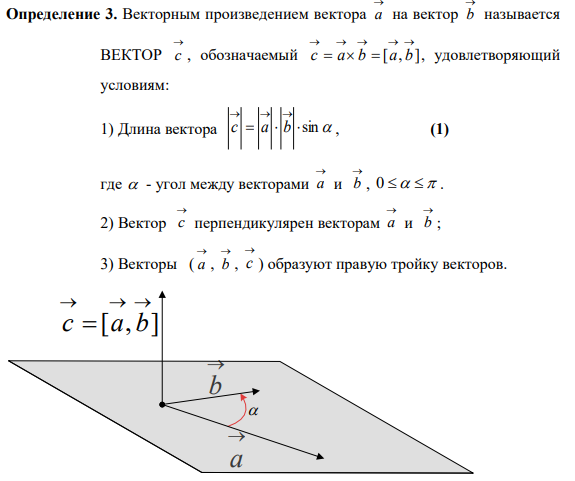
15. Векторное произведение векторов, его свойства и геометрический смысл. Координатная форма векторного произведения. Условие коллинеарности векторов через векторное произведение. Нахождение площади параллелограмма и треугольника с помощью векторного произведения.

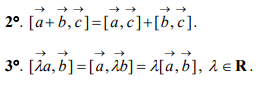
Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

Площадь параллелограмма, построенного на двух вектора, равно модулю их векторного произведения, а треугольник равен 1/2 модуля их векторного произведения.

1 6. Смешанное произведение векторов: определение, свойства, координатная форма и геометрический смысл. Условие компланарности тройки векторов. Нахождение объемов параллелепипедов и тетраэдров.

Модуль смешанного произведения

векторов равен объему параллелепипеда,

построенного на этих векторах.

1/6 модуля смешанного произведения равна

объему тетраэдра, построенного на этих

векторах.

1 7. Виды уравнений прямой на плоскости: каноническое и параметрическое уравнения, общее уравнение, уравнение прямой с угловым коэффициентом, уравнение прямой в отрезках. Условия параллельности и перпендикулярности прямых на плоскости для различных видов уравнений.

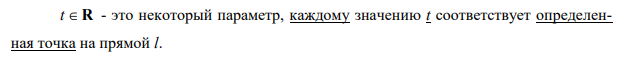
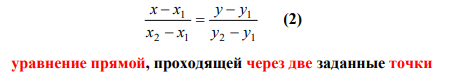
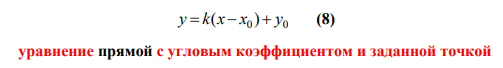
Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

   

18. Общее уравнение плоскости. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору (заданной прямой). Уравнение плоскости, проходящей через заданную точку, параллельно двум неколлинеарным векторам. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой. Взаимное расположение двух плоскостей. Угол между плоскостями.