ответы. Матан

1. Определение предела последовательности. Подпоследовательность, частичный предел.

Частичный предел некоторой последовательности — это предел одной из её подпоследовательностей, если только он существует.

2. Критерий Коши. Свойства сходящихся последовательностей. Теорема о пределе промежуточной последовательности.

Сходящаяся последовательность — это последовательность элементов множества {\displaystyle X}, имеющая предел в этом множестве.

Свойства:

1. Сходящаяся последовательность имеет единственный предел

2. Сходящаяся последовательность ограничена

3. Монотонная и ограниченная последовательность сходится.

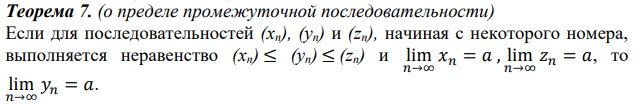
3. О пределение предела функции. Теорема о пределе промежуточной функции. Первый замечательный предел.

Определения предела по Коши и по Гейне являются эквивалентными

Теорема о пределе промежуточной функции:

4. Бесконечно малые функции. Теорема о связи бесконечно малых и бесконечно больших функций.

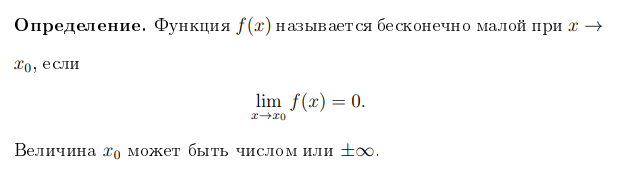
5. Теорема о пределе произведения бесконечно малой и ограниченной функций.

6. Второй замечательный предел. Раскрытие неопределенностей .

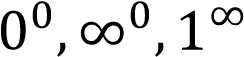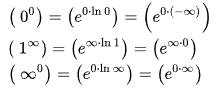
Для раскрытия неопределённостей видов  {\displaystyle \left(~0^{0}\right)} пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

7. Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные эквивалентности.

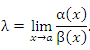  Пусть     и     – бесконечно малые функции при   . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении  x  точке  a  можно использовать предел отношения

Е сли этот предел представляет собой конечное ненулевое число, то     и     называются бесконечно малыми одного и того же порядка. Особый интерес представляет частный случай, когда  λ = 1. Тогда говорят, что     и    являются эквивалентными бесконечно малыми при   и записывают это утверждение в виде

8. Т еорема о разности эквивалентных бесконечно малых. Теорема о замене эквивалентности в пределе отношения.

9. Непрерывность функции в точке. Теорема о непрерывности арифметических действий, о непрерывности сложной функции.

Определение: функция непрерывна в точке  , если предел функции в данной точке равен значению функции в этой точке: .

Определение детализируется в следующих условиях:

1) Функция должна быть определена в точке  , то есть должно существовать значение  .

2) Должен существовать общий предел функции  . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов:  .

3 ) Предел функции в данной точке должен быть равен значению функции в этой точке:  .

10. Н епрерывность функции на отрезке. Свойства функций, непрерывных на отрезке.

11. Точки разрыва и их классификация.

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции называется точкой разрыва функции.

Если в точке a существуют конечные пределы f(a−0) и f(a+0), такие, что f(a−0)≠f(a+0), то точка a называется точкой разрыва первого рода.

Если хотя б один из пределов f(a−0) или f(a+0) не существует или равен бесконечности, то точка a называется точкой разрыва второго рода

Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции f(x) в точке a: f(a)≠f(a−0)=f(a+0) или функция f(x) не определена в точке a, то точка a называется точкой устранимого разрыва.

12. П роизводная, ее геометрический и механический смысл.

(Механический смысл производной)

Пусть задан путь s=f(x) движения материальной точки. Скорость данной материальной точки в момент времени t есть производная от пути s по времени t

13. Т еорема о связи непрерывности и дифференцируемости.

14. Арифметические действия с производными.

15. Таблица производных.

16. П роизводные сложной и обратной функций.

17. Д ифференциал, его связь с производной, геометрический смысл, инвариантность.

18. Теорема Ролля, ее геометрический смысл.

Теорема Ролля утверждает, что любая действительная дифференцируемая функция, принимающая одинаковые значения на концах интервала, должна иметь в этом интервале хотя бы одну стационарную точку, т.е. точку, в которой первая производная равна нулю. Геометрически это означает, что касательная к графику функции в этой точке горизонтальна

19. Теорема Лагранжа, ее геометрический смысл. Теорема Коши.

Теорема Лагранжа о среднем значении утверждает, что если функция f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), то в этом интервале существует хотя бы одна точка x=ξ, такая, чтоf(b)−f(a)=f′(ξ)(b−a).Данная теорема называется также формулой конечных приращений, поскольку она выражает приращение функции на отрезке через значение производной в промежуточной точке этого отрезка.

Теорема Лагранжа имеет простой геометрический смысл. Хорда, проходящая через точки графика, соответствующие концам отрезка a и b, имеет угловой коэффициент, равныйk=tanα=f(b)−f(a)b−a.Тогда внутри отрезка [a,b] существует точка x=ξ, в которой касательная к графику функции параллельна хорде.

20. П равило Лопиталя.

21. 2 2. Многочлен Тейлора, формула Тейлора. Остаточный член формулы Тейлора в формах Пеано и Лагранжа

23. Л окальный экстремум функции одного переменного. Необходимое и достаточное условия экстремума.

24. Г еометрический смысл второй производной. Точки перегиба.

25. А симптоты графика функции. Существование наклонной асимптоты.

26. Ч астные производные функции нескольких переменных. Теорема о равенстве смешанных производных.

27. Д ифференцируемостъ функции нескольких переменных. Дифференциал.

28. Л окальный экстремум функции нескольких переменных. Необходимое условие экстремума.