
Зайцева / 3 раздел
.pdf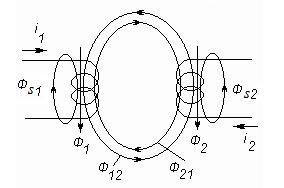
катушку, но и от токов, протекающих через другие индуктивно связанные с ней катушки.
Будем идеализировать свойства реальных катушек с индуктивными связями, считая, что они не рассеивают энергию (не содержат резистивного сопротивления), и что каждая катушка характеризуется только своей
индуктивностью. |
|
|
|
Рассмотрим две |
индуктивно |
||
связанные катушки (рис. 3.18). |
|||
Поток самоиндукции первой |
|||
катушки Ф11, вызванный током 1, |
|||
состоит из потока рассеяния |
Ф 1, |
||
который сцеплен только с витками |
|||
первой катушки, и взаимного |
|||
потока Ф12, сцепленного с витками |
|||
второй |
катушки, |
то |
есть |
Ф11 = Ф 1 + Ф12 . Аналогично для |
|
||
второй катушки Ф22 |
= Ф 2 |
+ Ф21. |
Рис. 3.18. Индуктивно связанные |
|
|
|
|
катушки
Потоки Ф12 и Ф21 называют потоками взаимной индукции. Их принято обозначать двумя индексами: первый указывает номер тока, вызвавшего данный поток, второй – с какой катушкой сцепляется поток. Например, поток Ф12 вызван током 1, сцепляется со второй катушкой.
Таким образом, суммарный поток, сцепленный с первой катушкой:
Ф1 = Ф11 ± Ф21,
а суммарный поток, сцепленный со второй катушкой:
Ф2 = Ф22 ± Ф12.
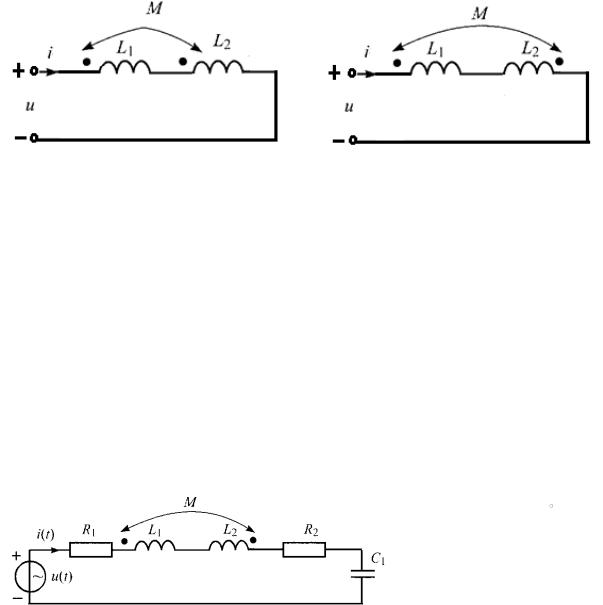
Знак " + " или " − " зависит от взаимного направления потоков, которые могут быть определены по правилу правой руки и которые зависят от взаимного расположения и направления намотки катушек. Для указания согласного (знак " + ") или встречного (знак " − ") направления потоков взаимной индукции на схемах применяют специальные обозначения – калибровочные метки в виде точек, звездочек у одного из зажимов катушки. Помечаются те зажимы катушек, через которые токи катушек должны проходить в одном и том же направлении для того, чтобы потоки взаимной индукции складывались. Эти зажимы называются однополярные.
Таким образом, если токи катушек ориентированы одинаково (или оба входят или оба выходят) относительно однополярных зажимов, то это согласное включение (рис. 3.19, а), в противном случае – встречное
(рис. 3.19, б).

а) |
б) |
Рис. 3.19. Схемы включения индуктивно-связанных катушек: |
|
а) согласное |
|
б) встречное |
|
Потокосцепления первой Ψ1 и второй Ψ2 |
катушек могут быть записаны |
следующим образом:
Ψ1 = Ф1 1 = Ф11 1 ± Ф21 1 = 1 1 ± 2 Ψ2 = Ф2 2 = Ф22 2 ± Ф12 2 = 2 2 ± 1,
где 1 и 2 индуктивности катушек; – взаимная индуктивность (Гн), которая является коэффициентом пропорциональности между потокосцеплением взаимной индукции и током, вызывающим это потокосцепление, при этом в линейных цепях взаимная индуктивность
21 = 12 = .
Соотношения для напряжений и токов на внешних зажимах двух индуктивно связанных идеализированных катушек имеет вид:
= |
Ψ1 |
|
= |
|
1 |
|
± |
2 |
; |
||||
|
|
|
|
|
|
|
|
||||||
1 |
|
1 |
|
|
|
|
|||||||
= |
|
Ψ2 |
= |
|
|
2 |
± |
|
1 |
. |
|||
|
|
2 |
|
||||||||||
2 |
|
|
|
|
|
|
|
||||||
Каждое напряжение состоит из двух слагаемых, первое из которых – напряжение самоиндукции, вызванное собственным током катушки, а второе – напряжение взаимной индукции, вызванное током другой катушки.
Степень магнитной связи двух катушек характеризуется коэффициентом связи, который равен среднегеометрическому значению относительных величин потоков взаимной индукции:
= √Ф21Ф12 ≤ 1
Ф11Ф22
Учитывая, что
Ф12 = 1/2; Ф21 = 2/1; Ф11 = 1 1/1; Ф22 = 2 2/2,
получим:
= . √ 1 2
При K=1 имеется совершенная связь – потоки рассеяния отсутствуют и весь поток является потоком взаимной индукции, сцепленным с витками обеих катушек. Отсутствию магнитной связи между катушками соответствует K=0.
Для режима гармонических колебаний уравнения могут быть записаны для комплексных токов и напряжений в следующем виде:
1̇= ω 1 ∙ 1̇± ω ∙ 2̇;2̇= ω 2 ∙ 2̇± ω ∙ 1̇.
Рассмотрим последовательное соединение индуктивно связанных катушек при согласном (рис. 3.20, а) и встречном (рис. 3.20, б) включении.
а) б)
Рис. 3.20. Последовательное соединение индуктивно связанных катушек при согласном (а) и встречном (б) включении
Через обе катушки проходит один и тот же ток. Напряжение на входе
цепи равно сумме напряжений ветвей: |
|
|
|
|
||||
̇ ̇ |
̇ |
|
̇ |
|
̇ |
|
̇ |
̇ |
= |
+ |
= ω ∙ ± ω ∙ + ω ∙ ± ω ∙ = |
||||||
1 |
2 |
1 |
|
|
|
2 |
|
|
|
|
= ω( + ± 2 ) ∙ .̇ |
|
|
|
|||
|
|
|
1 |
2 |
|
|
|
|
Знак плюс относится к согласному, |
а знак минус – к встречному |
|||||||
включению катушек. Таким образом, при последовательном соединении катушек эквивалентная индуктивность: э = 1 + 2 ± 2 при наличии магнитной связи при согласном включении увеличивается на 2 и уменьшается на ту же величину при встречном включении катушек.
Пример 3.10.1
u(t) 30cos(105 t 20 ), В
R1 R2 150 Ом
L1 5 мГн, L2 1 мГн M 2 мГн
C1 20 нФ
Рис. 3.21. Схема электрической цепи
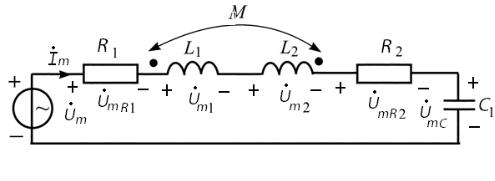
В индуктивно-связанной цепи, представленной на рис. 3.21, найдем
к
оПрименим символический метод.
м |
Перейдем |
к |
комплексной |
|
схеме |
замещения |
цепи |
(рис. 3.22). |
||||||||
Определим параметры цепи: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
л |
|
|
|
|
̇ |
= 30 ∙ − 200, В |
|
|
|
|
|
|||||
е |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
= − |
= − |
|
|
|
= − 500, Ом |
|
||||||||
|
|
|
|
|
|
|||||||||||
к |
|
ω |
105 ∙ 20 ∙ 10−9 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
с |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
Рис. 3.22. Комплексная схема замещения цепи |
|
|||||||||||||
н |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
Запишем второй закон Кирхгофа для приведенной цепи: |
|
||||||||||||||
е |
|
|||||||||||||||
|
|
̇ = ̇ |
|
+ ̇ + ̇ |
+ ̇ |
|
|
+ ̇ . |
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
1 |
2 |
2 |
|
|
|
|||||
с |
Выразим напряжения на резистивных |
сопротивлениях |
и емкости, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
используя закон Ома в комплексной форме: |
|
|
|
|
|
|
|
|||||||||
о |
̇ |
= ∙ ̇, |
̇ |
|
= ∙ ̇, |
̇ |
|
= ∙ ̇. |
|
|||||||
п |
|
|
|
|||||||||||||
1 |
|
1 |
|
2 |
|
2 |
|
|
|
|
|
|
||||
рНапряжения на индуктивностях с учетом магнитной связи между ними
запишем следующим образом:
о
т |
̇ |
|
= |
∙ ̇ − ∙ ̇; |
|||
1 |
|
1 |
|
|
|
||
и |
̇ |
= − ∙ ̇ + |
2 |
∙ ̇. |
|||
в |
2 |
|
|
|
|
|
|
Катушки включены встречно, |
поэтому в |
выражениях стоит знак |
|||||
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
«минус». Катушки соединены последовательно, поэтому через них |
|||||||||||||
протекает один и тот же ток ̇. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
Таким образом, входное напряжение ̇ |
будет равно: |
|
||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
̇ |
= |
∙ ̇ + ω ∙ ̇ − ω ∙ ̇ |
− ω ∙ ̇ |
+ ω |
∙ ̇ + |
||||||||
е |
|
1 |
|
|
1 |
|
|
|
|
|
2 |
|
|
+ ∙ ̇ + ∙ ̇ = ̇ |
∙ ( + + + ω ∙ ( + − 2 ∙ )). |
||||||||||||
|
|
2 |
|
|
|
1 |
2 |
|
|
1 |
2 |
||
ц |
Из этого выражения можно выразить вх( ω): |
|
|
||||||||||
|
|
|
|
|
̇ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
( ω) = |
|
= + + + ω ∙ ( + − 2 ∙ ). |
|||||||
|
|
|
|||||||||||
п |
|
вх |
|
|
̇ |
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иПодставив численные значения, получаем:
Z |
( ω) = 150 + 150 − 500 + 105 ∙ (5 ∙ 10−3 + 1 ∙ 10−3 − 2 ∙ 2 ∙ 10−3) = |
||
вх |
|
|
∙ − 450, Ом |
в |
= 300 − 300 = 300 ∙ √2 |
||
х |
Рассчитаем комплексную амплитуду тока ̇: |
||
j |
|
|
|
|
|
|
|
ω |
|
|
|
и |
|
|
|
т |
|
|
|
о |
|
|
|

|
̇ |
|
30 ∙ − 200 |
|
0 |
|||
̇ = |
|
= |
|
|
|
= 0.07 ∙ 25 , А |
||
|
|
|
|
|
||||
|
вх( ω) |
|
300 ∙ √2 ∙ − 450 |
|
|
|||
|
|
|
|
|||||
Перейдем к мгновенному значению тока ( ): |
|
|||||||
|
( ) = 0.07 cos(105 + 250), |
|
||||||
3.11. Трансформатор с воздушным сердечником. Уравнение трансформатора. Т-образная схема замещения трансформатора
Трансформатором называется устройство, предназначенное для преобразования переменных напряжений и токов.
Трансформаторы состоят из двух или нескольких индуктивно связанных катушек или обмоток, расположенных на общем сердечнике, выполненном из ферромагнитного или неферромагнитного материала.
Рассмотрим простейший двухобмоточный трансформатор без сердечника. Такой трансформатор принято называть трансформатором с воздушным сердечником.
Обмотка трансформатора, к которой подводится входное напряжение1, называется первичной обмоткой. Обмотка, к которой присоединяется нагрузка, - вторичной. Число витков первичной обмотки равно 1, а число витков вторичной обмотки - 2.
Электромагнитная энергия из первичной обмотки во вторичную передается путем взаимоиндукции.
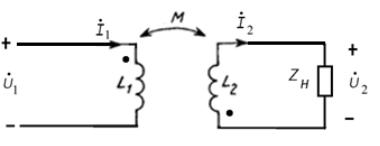
Рассмотрим трансформатором с воздушным сердечником без потерь, когда две индуктивно связанные катушки имеют общую точку (рис. 3.23, а).
Получим Т-образную схему замещения воздушного трансформатора без потерь (рис. 3.23, б), в которой отсутствуют индуктивные связи и которой удобно пользоваться для расчета цепей с использованием различных методов.
а) б)
Рис. 3.23. Схема воздушного трансформатора без потерь (а) и его Т-образная схема замещения (б)
Составив уравнения по первому и второму законам Кирхгофа, можно найти условия, при которых схема на рис. 3.23, б будет полностью эквивалента схеме на рис. 3.23, а.

Уравнения для схемы на рис. 3.23, а можно записать в следующем
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
̇ |
= ω ∙ ̇± ω ∙ ̇; |
|
|
|
|
|||||
|
|
|
1 |
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
̇ |
|
|
̇ |
|
̇ |
|
|
|
|
|
|
|
|
|
= ± ω ∙ + ω |
∙ . |
|
|
|
|
|||||
|
|
|
|
2 |
|
|
1 |
2 |
2 |
|
|
|
|
|
Уравнения для схемы на рис. 3.23, б: |
|
|
|
|
|
|
||||||||
|
̇ |
= ω |
∙ ̇+ ω |
∙ ( ̇+ ̇) = ω( |
+ ) ∙ ̇+ ω |
|
∙ ̇; |
|||||||
{ |
1 |
а 1 |
|
1 |
2 |
|
|
а |
|
1 |
|
2 |
||
̇ |
= ω |
̇ |
̇ |
|
∙ |
̇ |
= ω |
|
̇ |
|
+ |
|
̇ |
|
|
|
∙ ( + ) + ω |
|
|
∙ + ω( |
) ∙ . |
||||||||
|
2 |
|
1 |
2 |
2 |
|
1 |
с |
|
|
2 |
|||
Эти уравнения равнозначны при выполнении следующих условий:
1 = а ± ;= ± ;
2 = с ± .
Из этих соотношений можно найти параметры Т-образной схемы замещения индуктивно-связанных катушек (рис. 3.24):
Полученную схему называют Т-образной схемой замещения трансформатора, параметры которого не исключают возможности появления отрицательной индуктивности.
Рис. 3.24. Т-образная схема замещения индуктивно-связанных катушек
Наличие отрицательной индуктивности в рассмотренной схеме замещения цепи не препятствует применению последней при анализе колебаний в цепи, хотя и свидетельствует о невозможности физического осуществления цепи по такой схеме на пассивных элементах.
Рассмотрим воздушный трансформатор с потерями, у которого вторичная обмотка нагружена на комплексное сопротивление н (рис. 3.25):
н = н + н.
Рис. 3.25. Схема воздушного трансформатора с потерями

|
Введем обозначения: |
|
|
|
|
|
|
|
ω1 = 1, |
н + 2 |
= 22, |
2 + н = 22, |
|||
где н и н – активное и реактивное сопротивления нагрузки; |
|||||||
22 и |
22 – активное и реактивное сопротивления вторичного контура. |
||||||
|
Запишем уравнения по второму закону Кирхгофа для первичного и |
||||||
вторичного контуров: |
|
|
|
|
|
|
|
|
{ |
̇ = |
∙ ̇+ |
∙ ̇+ ω ∙ ̇; |
|||
|
1 |
1 |
1 |
1 |
1 |
2 |
|
|
|
∙ ̇+ |
∙ ̇+ |
∙ ̇= 0. |
|||
|
|
|
1 |
22 |
1 |
22 |
2 |
Решая эту систему уравнений относительно тока 1̇, получаем:
̇1̇= (1 + вн) +1(1 + вн),
где
вн = ( )2∙ 22 − вносимое активное сопротивление из второго контура в
222+ 222
первый;
вн = − ( )2∙ 22 – вносимое реактивное сопротивление из второго контура
222+ 222
в первый.
Вносимое активное сопротивление всегда больше нуля. В нем поглощается энергия, которая в реальной цепи передается из первичной цепи во вторичную. Вносимое реактивное сопротивление имеет знак, противоположный знаку 22, то есть оно может быть как больше, так и меньше нуля.
Рассмотрим трансформатор с воздушным сердечником с потерями в режиме холостого хода (рис. 3.26):
Рис. 3.26. Схема трансформатора в режиме холостого хода
Уравнения по второму закону Кирхгофа для первичного и вторичного контуров можно получить, используя второй закон Кирхгофа, считая
2̇= 0:
|
{ |
̇ |
= ∙ ̇+ ∙ ̇; |
|
|
||||||||||
|
1 |
|
1 |
|
1 |
|
1 1 |
|
|
|
|||||
|
|
|
|
|
|
ω ∙ ̇= ̇. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
Коэффициент трансформации S может быть найден: |
|||||||||||||||
|
̇ |
|
|
|
|
ω ∙ ̇ |
|
|
ω |
|
|
||||
= |
2 |
|
= |
|
|
|
|
1 |
|
̇= |
|
|
|
. |
|
̇ |
|
|
̇ |
|
∙ |
+ |
|||||||||
|
|
|
|
|
∙ |
+ |
|
|
1 |
1 |
|
||||
|
1 |
|
|
1 |
1 |
|
1 |
1 |
|
|
|
|
|||
Сопротивлением 1 |
можно пренебречь, поскольку ω 1 = 1 1. |
|||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
ω |
= |
|
= |
|
√ 1 ∙ 2 |
= ∙ √ |
2 |
= , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где = √ |
2 |
= |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При «жесткой» магнитной связи = 1 коэффициент трансформации |
||||||||||||||||||||||||||
равен: |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
= = |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 > 1, |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Если |
число |
витков |
|
|
то |
мы |
имеем |
повышающий |
||||||||||||||||||
трансформатор, выходное напряжение в раз больше входного. |
|
|||||||||||||||||||||||||
Если число витков |
2 |
< 1, |
то трансформатор |
понижающий, |
||||||||||||||||||||||
выходное напряжение в раз меньше входного. |
|
|
|
|
|
|
|
|
||||||||||||||||||
Совершенный |
трансформатор ( 1 = 2 = 0; = 1 ), |
у |
которого |
|||||||||||||||||||||||
бесконечно |
большие значения |
|
индуктивностей, |
называется |
идеальным |
|||||||||||||||||||||
(рис. 3.27). |
Отношения |
токов |
и |
напряжения |
в |
таком трансформаторе |
||||||||||||||||||||
определяется выражениями, т.е. |
|
̇ |
|
|
|
|
̇ |
|
̇ |
= |
|
̇ |
1 |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
= ∙ ; |
|
|
|
∙ |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
|
|
1 |
|
|
|
|
|
|||||
Рис. 3.27. Схема идеального трансформатора
Полная мощность первичной цепи трансформатора равна полной мощности вторичной цепи:
̃ |
̇ ̇ |
|
̇ |
1 |
̇ |
|
|
|
̇ ̇ |
̃ |
||
1 = 1 1 |
= 2 |
2 |
= 2 2 |
= 2. |
||||||||
Входное сопротивление идеального трансформатора, нагруженного на |
||||||||||||
сопротивление н (рис. |
3.27) : |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
̇ |
̇ |
∙ |
|
|
|
||||
|
|
|
2 |
|
|
|
||||||
|
= |
1 |
= |
|
|
= |
н |
. |
|
|||
|
|
|
|
|
|
|
||||||
|
вх |
|
1̇ |
2̇∙ |
2 |
|
||||||
|
|
|
|
|||||||||
Таким образом, идеальный трансформатор преобразует уровни напряжений и тока в раз при неизменной мощности, а также изменяет модуль сопротивления нагрузки в 2 раз.
Приблизиться к условиям, при которых трансформатор является идеальным, можно применяя большое число витков и сердечник с высокой магнитной проницаемостью.
Контрольные вопросы
1.Сформулируйте определения понятий: амплитуда, период, частота, угловая частота, фаза, начальная фаза гармонического колебания.
2.Что называют действующим значением периодического колебания? Чему равно действующее значение гармонического колебания?
3.Как определяется средняя мощность гармонических колебаний?
4.Какими соотношениями связаны амплитуды (действующие значения) гармонических тока и напряжения на резистивном сопротивлении, индуктивности, емкости?
5.Как сдвинуты по фазе ток и напряжение на резистивном сопротивлении, индуктивности, емкости?
6.Как комплексная амплитуда связана с мгновенным значением гармонического колебания? Как мгновенное значение связано с комплексной амплитудой?
7.Запишите комплексные сопротивления резистивного сопротивления, индуктивности и емкости.
8.Какой физический смысл имеет модуль, аргумент, вещественная и мнимая части комплексного сопротивления цепи?
9.Какие значения может принимать аргумент комплексного
сопротивления пассивной цепи?
10.Что понимают под комплексной мощностью? Что означает ее вещественная и мнимая части?
11.Запишите условия баланса активной (средней) и реактивной мощностей.
12.Какое явление называется явлением взаимоиндукции?
13.Каковы особенности составления уравнений для линейных цепей с индуктивными связями?
