
Зайцева / 3 раздел
.pdf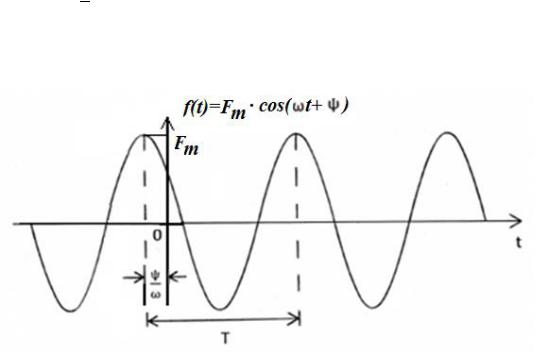
3.АНАЛИЗ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
ВЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Гармонические напряжения и токи в электрических цепях. Мгновенная и средняя мощности гармонических колебаний. Гармонические колебания в элементах электрических цепей. Гармонические колебания в последовательном колебательном контуре. Символическое изображение косинусоидальных функций комплексными числами. Законы Кирхгофа в комплексной форме. Закон Ома в комплексной форме. Комплексные сопротивления и проводимости. Символический метод анализа гармонических колебаний. Применение символического метода для расчёта мощности. Уравнение баланса средней мощности. Условие получения в нагрузке генератора гармонических колебаний максимальной средней мощности. Система узловых уравнений для комплексных амплитуд колебаний. Цепи со взаимными индуктивностями. Особенности составления уравнений для цепей с магнитными связями. Трансформатор с воздушным сердечником. Уравнение трансформатора. Т- образная схема замещения трансформатора.
3.1. Гармонические напряжения и токи в электрических цепях
Гармоническое колебание ( ), мгновенное значение которого может быть описано одной из функций
( ) = ∙ cos(ω + ѱ); ( ) = ∙ sin(ωt + ƺ),
если ƺ = ѱ + π2.
Обе записи равноправны, однако мы будем пользоваться первой. График колебания ( ) показан на рис. 3.1.
Рис. 3.1. График гармонического колебания

Наибольшее по абсолютному значению отклонение колеблющейся величины называется её амплитудой и обозначается . Наименьшее значение времени, после которого процесс полностью повторяется (время одного цикла колебания), называется периодом колебания Т (рис. 3.1). Число циклов колебания в единицу времени называется циклической частотой колебания или просто частотой. Частота измеряется в герцах (Гц). Герц – одно колебание в секунду. Число циклов колебания в интервале, равном 2π единицам времени, называется угловой частотой , ω = 2π =
2π.
Величина (ω + ѱ) называется фазой колебания. Значение фазы колебания в момент времени = 0 называется начальной фазой колебания ѱ, которая может быть как положительной, так и отрицательной вещественной величиной. Она измеряется относительно начала отсчета времени.
При сравнении гармонических колебаний равных частот в одной и той же цепи
1( ) = 1 ∙ cos(ω + ѱ1) и 2( ) = 2 ∙ cos( + ѱ2)
отдельно сопоставляются амплитуды и фазы колебаний. При сопоставлении
амплитуд колебаний используется их отношение 1, а при сопоставлении
2
фаз – их разность φ = ѱ1 − ѱ2.
Разность фаз или сдвиг фаз φ не зависит от начала отсчета времени и может принимать как положительные, так и отрицательные значения.
Для наглядного суждения о соотношении между амплитудами и начальными фазами гармонических колебаний равных частот в одной и той же цепи используется векторная диаграмма. На ней в полярной системе координат каждому гармоническому колебанию соответствует радиусвектор, длина которого в выбранном масштабе пропорциональна амплитуде колебания, а полярный угол равен начальной фазе колебания. Принято положительные значения углов отсчитывать против часовой стрелки, а отрицательные – по часовой стрелке.
На рис. 3.2 приведены графики гармонических колебаний 1( ) и 2( )
ивекторная диаграмма для случая, если φ = ѱ1 − ѱ2 > 0, что означает, что колебание 2( ) отстает от колебания 1( ) по фазе на угол φ.
На рис. 3.3 приведены графики гармонических колебаний 1( ) и 2( )
ивекторная диаграмма для случая, если φ = ѱ1 − ѱ2 < 0, что означает, что
колебание 2( ) опережает от колебания |
1( ) по фазе на угол |
|φ| = |ѱ1 − ѱ2|. |
|
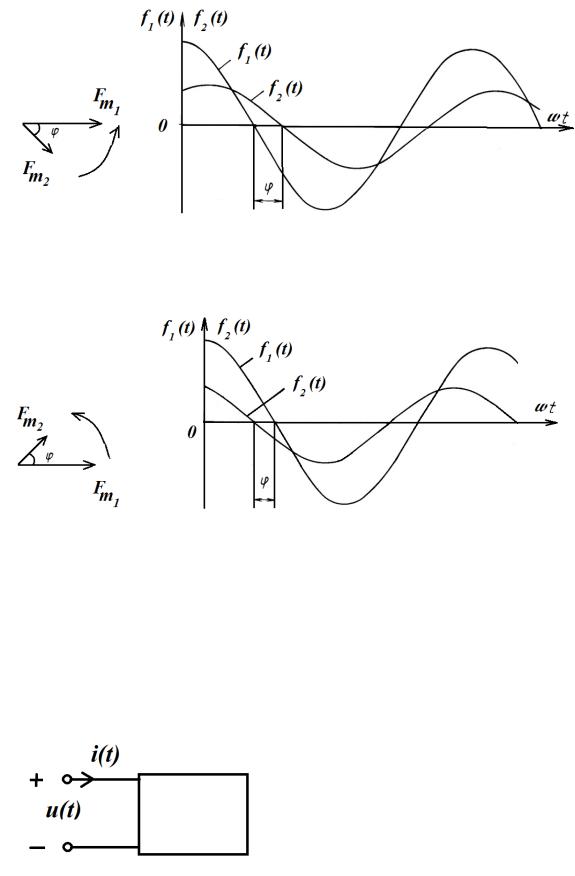
Рис. 3.2. Графики гармонических колебаний 1( ) и 2( ) и векторная диаграмма при φ = ѱ1 − ѱ2 > 0
Рис. 3.3. Графики гармонических колебаний 1( ) и 2( ) и векторная диаграмма при φ = ѱ1 − ѱ2 < 0
3.2. Мгновенная и средняя мощности гармонических колебаний
Мгновенные значения напряжения и тока на входе линейного двухполюсника (рис. 3.4), находящегося в режиме гармонических колебаний, имеют вид:
( ) = ∙ cos(ω + ѱ );
( ) = ∙ cos(ω + ѱ ).
Рис. 3.4. Линейный двухполюсник

При согласном выборе положительных направлений напряжения и тока на входе двухполюсника мгновенная мощность, потребляемая двухполюсником, равна
( ) = ( ) ∙ ( ) = |
∙ cos(ω + ѱ |
|
) ∙ |
∙ cos(ω + ѱ |
) = |
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
∙ |
|
|
|
∙ |
|
|
|
|
|
= |
|
|
∙ cos( ѱ − ѱ ) + |
|
|
∙ cos(2ω + ѱ + ѱ ). |
|||||
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|||||
Очевидно, что в режиме гармонических колебаний мгновенная мощность, потребляемая двухполюсником, содержит постоянную составляющую, относительно которой она колеблется с частотой 2ω.
В пассивных RL-цепях значения мгновенной мощности в одной части полупериода колебания положительны (цепь потребляет энергию), а в другой его части – отрицательны (цепь отдает энергию, запасенную в магнитном и (или) электрическом полях элементов индуктивности и емкости).
Для периодических колебаний широко используется понятие средней мощности
|
1 |
|
1 |
|
= |
|
∫0 ( ) = |
|
∫0 ( ) ∙ ( ) . |
|
|
В случае рассматриваемого режима гармонических колебаний это постоянная составляющая в последнем выражении, т.е.
|
|
∙ |
|
= = |
|
|
∙ cosφ, |
|
|
||
ср |
2 |
|
|
где φ = ѱ − ѱ .
В электрических цепях широко применяются среднеквадратические значения напряжений и токов, которые называют действующими (эффективными):
|
1 |
|
|
|
|
|
|
|
|
|||||
= √ |
|
|
∫ 2 = |
|
|
|
|
|
= 0,707 ∙ |
|
; |
|||
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
√2 |
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|||||
= √ |
|
|
∫ 2 = |
|
|
|
= 0,707 ∙ |
, |
|
|||||
|
|
|
|
|
|
|||||||||
|
|
0 |
√2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
тогда выражение для средней мощности имеет вид:
= ср = ∙ ∙ cosφ.
Для пассивных двухполюсников средняя мощность не может принимать отрицательные значения, т.е. ≥ 0, поэтому разность фаз между гармоническими напряжением и током на зажимах пассивного двухполюсника не может выходить за пределы

π π
−2 ≤ φ ≤ 2.
3.3.Гармонические колебания в элементах электрических цепей
Пусть через некоторый пассивный элемент электрической цепи проходит гармонический ток
( ) = ∙ cos(ω + ѱ ).
Найдем соотношения между амплитудами и начальными фазами гармонических колебаний напряжения и тока в элементе, при согласованном выборе их положительных направлений.
В резистивном сопротивлении: Для мгновенных значений
( ) = ∙ ∙ cos(ω + ѱ ) = ∙ cos(ω + ѱ ),
где ѱ = ѱ ; для амплитудных значений = ∙ ;
для действующих значений = ∙ .
Из этих соотношений следует, что закон Ома выполняется для мгновенных, амплитудных и действующих значений напряжения и тока в резистивном сопротивлении. Фазы колебаний напряжения и тока совпадают (находятся в фазе), а значит, угол сдвига фаз ѱ − ѱ = 0, а cosφ = 1.
Выделяемая в резистивном сопротивлении мощность всегда
положительна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ |
|
|
∙ |
|
|
2 |
∙ |
|
|
2 |
∙ |
|
= |
|
|
∙ cosφ = |
|
|
= |
|
|
= |
|
|
> 0, |
||
2 |
2 |
|
2 |
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
для действующих значений
= ∙ = 2 ∙ = 2 ∙ > 0.
Векторная диаграмма и временные диаграммы мгновенных значений напряжения, тока и мощности в резистивном сопротивлении приведены на рис. 3.5.
а) б) в)
Рис. 3.5. Векторная диаграмма (а), временные диаграммы мгновенных значений напряжения, тока (б) и мощности (в) в резистивном сопротивлении
В индуктивности:

Напряжение будет изменяться по закону:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) = |
|
|
= − |
|
|
∙ ω ∙ sin(ω + ѱ |
) = |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
= |
∙ ω ∙ cos (ω |
+ ѱ |
|
+ |
) = |
∙ cos(ω + ѱ |
|
). |
||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, закон Ома выполнятся в индуктивности только для |
||||||||||||||||
амплитудных |
|
= ω ∙ |
|
и действующих значений = ω ∙ . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сравнение |
|
мгновенных |
значений |
гармонических |
|
колебаний |
||||||||||
напряжения и тока показывает, что колебания напряжения опережают по
фазе колебания |
тока в индуктивности |
на |
угол |
|
, |
т.е. |
ѱ = ѱ + |
π |
, |
|||||
2 |
2 |
|||||||||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|||
следовательно, угол сдвига фаз φ = ѱ − ѱ = |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
Поскольку |
cosφ = cos |
= 0, то |
значение средней |
мощности |
в |
|||||||||
|
||||||||||||||
|
2 |
|
|
|
|
( = 0), |
|
|
|
|
||||
индуктивности |
оказывается |
равным |
нулю |
т.е. энергия |
в |
|||||||||
реактивном элементе не рассеивается и происходит обмен энергией между индуктивностью и внешней по отношению к ней целью.
Векторная диаграмма и временные диаграммы мгновенных значений напряжения, тока и мощности в индуктивности приведены на рис. 3.6.
В емкости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напряжение будет изменяться по закону: |
|
|
|
|
|
||||||||||||||
|
( ) = |
|
1 |
|
∫ |
= ∙ |
|
|
1 |
|
∙ sin(ω |
+ ѱ |
) = |
|
|
||||
|
|
|
ω |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= ∙ |
1 |
|
∙ cos (ω + |
ѱ |
|
– |
π |
) |
= |
∙ cos(ω + ѱ |
|
). |
|||||||
ω |
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) |
|
|
|
б) |
в) |
|
|
Рис. 3.6. Векторная диаграмма (а), временные диаграммы мгновенных значений |
|||||||
напряжения, тока (б) и мощности (в) в индуктивности |
|
||||||
Следовательно, закон Ома выполнятся в емкости только для |
|||||||
амплитудных |
= |
1 |
∙ |
и действующих значений = |
1 |
∙ . |
|
|
|
||||||
с |
|
ω |
с |
|
|
ω |
|
|
|
|
|
|
|
||
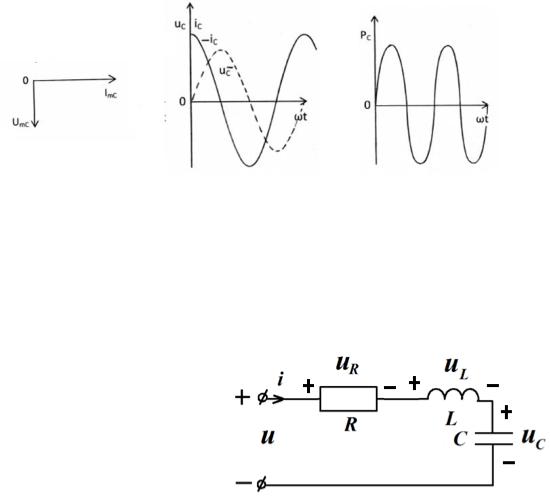
Сравнение мгновенных значений гармонических колебаний напряжения и тока показывает, что колебания напряжения отстают по фазе
от колебаний тока в емкости на угол |
|
, т.е. ѱ = ѱ − |
π |
, следовательно, угол |
||||||
2 |
2 |
|||||||||
|
π |
|
|
|
|
|
|
|||
сдвига фаз φ = ѱ − ѱ = − |
. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
2 |
|
π |
|
|
|
|
|
|
||
Поскольку cosφ = cos(− |
) = 0, то значение |
|
средней мощности в |
|||||||
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
емкости оказывается равным нулю ( = 0), т.е. |
энергия в реактивном |
|||||||||
элементе не рассеивается и происходит обмен энергией между емкостью и внешней по отношению к ней целью.
Векторная диаграмма и временные диаграммы мгновенных значений напряжения, тока и мощности в емкости приведены на рис. 3.7.
а) |
б) |
в) |
Рис. 3.7. Векторная диаграмма (а), временные диаграммы мгновенных значений напряжения, тока (б) и мощности (в) в емкости
3.4. Гармонические колебания в последовательном колебательном контуре
Электрическую цепь, содержащую соединенные последовательно резистивное сопротивление , индуктивность и емкость , называют последовательным RLC-контуром или последовательным колебательным контуром
(рис. 3.8).
Рис. 3.8. Схема последовательного колебательного контура
Пусть в контуре протекает гармонический ток
( ) = ∙ cos(ω + ѱ ),
и требуется найти гармоническое напряжение на входе контура
( ) = |
∙ cos( + ѱ |
|
), |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
т.е. найти амплитуду и начальную фазу ѱ |
|
напряжения. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Согласно второму закону Кирхгофа |
|
|
|
|
|
|
|
|
|||
− + |
+ |
+ |
= 0 |
или |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
= ∙ + |
|
|
+ |
|
|
∫ . |
|
||||
|
|
|
|||||||||
Подставив выражения, полученные в разделе 3.3, получим:
|
|
( ) = ∙ |
|
∙ cos(ω + ѱ |
) + ω ∙ |
∙ cos (ω + ѱ |
|
+ |
π |
) + |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
+ |
|
∙ |
|
∙ cos (ω |
+ ѱ |
|
– |
) = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
ω |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
= |
∙ cos(ω + ѱ |
|
) |
+ |
|
|
∙ cos(ω + ѱ |
|
) + |
∙ cos(ω + ѱ |
|
), |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где |
|
= |
∙ |
; |
|
= ω ∙ |
; = |
∙ |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ѱ = ѱ ; ѱ = ѱ + |
|
π |
; ѱ = ѱ – |
π |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
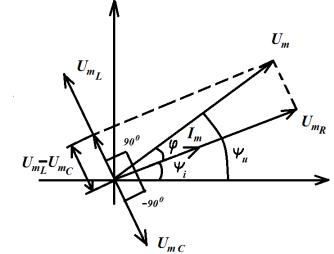
Для полученных выражений построим векторную диаграмму |
|||||||||||||||||||||||||||||||||||||||
напряжений и токов (рис. 3.9). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На векторной диаграмме |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
видно, что вектор напряжения |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
|
резистивном |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сопротивлении |
|
совпадает |
по |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направлению с вектором тока |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поскольку колебания тока |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и напряжения на R находятся |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в фазе. Векторы напряжений |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
повернуты |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно вектора тока на |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
углы |
+ |
π |
|
и − |
π |
, |
|
так |
|
как |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
колебания |
напряжения |
|
на |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зажимах |
индуктивности |
||||||||||||||||||||
Рис. 3.9. Векторная диаграмма напряжений |
|
|
|
опережают, |
а |
|
на |
|
зажимах |
||||||||||||||||||||||||||||||
|
|
|
емкости отстают по фазе на |
||||||||||||||||||||||||||||||||||||
|
|
и токов в RLC-контуре |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
угол |
|
|
|
π |
от |
|
|
|
колебаний |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
проходящего через них тока.
Следует иметь в виду, что векторная диаграмма и найденные с ее помощью численные решения будут верны только для одной частоты гармонических колебаний.
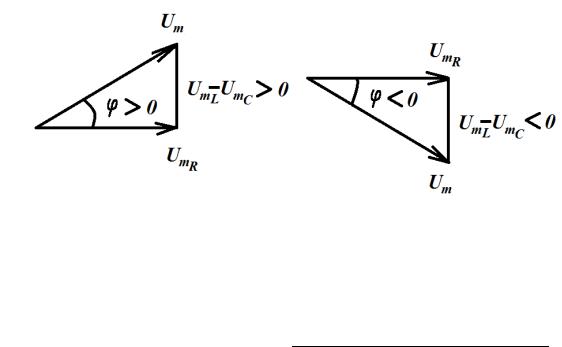
Очевидно, что треугольники напряжений в RLC-контуре могут быть двух видов: если > , то цепь носит индуктивный характер (приложенное напряжение опережает ток по фазе) (рис. 3.10, а), а если< , то цепь носит емкостной характер (приложенное напряжение отстает от тока по фазе) (рис. 3.10, б).
а) б)
Рис. 3.10. Векторные диаграммы напряжений в RLC-контуре: а) цепь носит индуктивный характер
б) цепь носит емкостной характер
По треугольнику напряжений находим амплитуду напряжения, приложенного ко всей цепи:
|
|
|
|
|
|
|
|
|
|
|
= √(ω ∙ − |
1 |
|
|
|
|
|
|||||||
|
= √( |
− |
)2 + |
2 |
|
∙ )2 |
|
+ ( ∙ )2 |
= |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
= ∙ √(ω − |
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
)2 + 2 = |
∙ √ 2 + 2 |
, |
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где = ω − |
1 |
|
– реактивное сопротивление цепи. |
|
|
|
|
|
||||||||||||||||
ω |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разделив правую и левую часть выражения для |
на , получим |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражение для модуля полного сопротивления цепи : |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
= = √ 2 |
+ 2 |
= √(ω − |
|
|
|
|
) + 2. |
|
||||||||||
|
|
|
|
|
|
|
ω |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пользуясь этим выражением, перейдем от треугольника напряжений к треугольнику сопротивлений, вид которого для индуктивного характера цепи показан на рис. 3.11, а, а для емкостного характера цепи – на рис. 3.11, б.

а) б) Рис.3.11. Треугольники сопротивлений в RLC-контуре:
а) цепь носит индуктивный характер б) цепь носит емкостной характер
Угол сдвига φ между напряжением и током на входе RLC-контура равен:
1
φ= arctg = arctg ω − ω ,
если φ > 0, то цепь имеет индуктивный характер (напряжение на входе цепи опережает ток, протекающий в ней). Если φ < 0, то цепь имеет емкостной характер (напряжение на входе цепи отстает от тока в этой цепи).
Таким образом, можно записать гармоническое напряжение, приложенное к RLC-контуру (рис. 3.8):
( ) = ∙ cos(ω + ѱ + φ) = ∙ cos(ω + ѱ ).
3.5. Символическое изображение косинусоидальных функций комплексными числами. Законы Кирхгофа в комплексной форме
Каждой косинусоидальной функции заданной частоты ω можно сопоставить вектор на комплексной плоскости. С другой стороны, каждый вектор можно записать в виде комплексного числа. Так, гармоническому колебанию ( ) = ∙ cos(ω +
ѱ) можно сопоставить радиусвектор ̇m на комплексной плоскости (рис. 3.12).
Рис. 3.12. Радиус-вектор ̇m на комплексной плоскости
Длина вектора в выбранном масштабе равна амплитуде колебания Um, а угол, образованный этим вектором с положительным направлением
