1. Введение

Что-то красиво написано

2. Составление схемы нагружения

Составление схемы нагружения начинается с расстановки действующих в этой схеме сил. Для примера рассмотрим промежуточный вал 5 типа редуктора (двухступенчатый цилиндрический редуктор; тихоходная ступень – прямозубая, быстроходная – косозубая), представленный на рисунке 1.

Рис.1

Опорами при расчёте вала будут являться подшипники. Силы реакции в опорах будут приложены к центру шарика подшипника. Считается, что усилия, действующие в зацеплении, распределены равномерно по линии контакта, следовательно, на схеме нагружения соответствующие силы приложены к середине зубчатого колеса. Для удобства выполнения расчетов валов и подшипниковых узлов, усилие, действующее в зоне контакта зубьев , представляют в виде составляющих, в общем случае действующих по трем взаимно-перпендикулярным направлениям: по касательной к начальным окружностям - окружной силы , по радиусу - радиальной сил 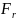, параллельно оси зубчатых колес - осевой силы .

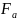Для прямозубой и косозубой цилиндрической передачи система сил действующих в зацеплении представлена формулами 1 и 2 соответственно.

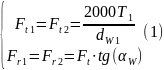
Где – стандартный угол зацепления. Крайне важно учесть, что в формулах 1 и 2 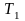- момент на шестерне пары зубчатых колес, образующих элементарную передачу.

Расстояния от точки опоры до действующих сил на рисунке 1 обозначены как 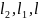. Стоит обратить внимание, что плечом для осевой силы будет являться радиус зубчатого колеса.

3. Определение сил реакции в опорах

Для того, чтобы система находилась в равновесии необходимо соблюдение условия равновесия:

Для определения сил реакции в опоре А, составляется уравнение моментов относительно неподвижной точки В. Для удобства, примем за точку А левый подшипник, а за точку В – правый. Тогда уравнение моментов в общем виде (без учёта знака) будет выглядеть следующим образом:

Уравнение 3 не имеет решений, т.к. содержит два неизвестных – 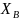и 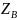. Для того, чтобы решить данное уравнение, необходимо рассмотреть его в двух плоскостях: XOY и ZOY. Таким образом, из уравнения 3 вытекают уравнения 4, 5, имеющие в своём составе по одному неизвестному.

Реакции в опоре В находят аналогичным образом.

Для проверки правильности найденных значений сил реакции в опорах, необходимо просуммировать все силы по соответствующим осям с учётом знака. Если полученная сумма равна нулю, то найденные значения сил соответствуют условию равновесия.

1. Плоскость XOY

В плоскости XOY находятся окружные силы , и сила . Составляя уравнение для плоскости XOY с учётом направления осей получаем:

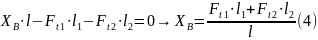
2. Плоскость ZOY

В плоскости ZOY находятся радиальные силы , осевая силы и сила . Составляя уравнение для плоскости ZOY с учётом направления осей получаем:

При составлении уравнения относительно неподвижной точки В следует помнить, что сила будет уже с противоположным знаком.

3. Определение суммарной реакции в опорах

Суммарная реакция в опорах находится согласно формуле 6.

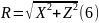
4. Определение изгибающих моментов

   1. Под колесом

Моменты под колесом определяются согласно формулам 7-9.

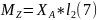
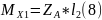
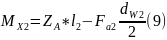
2. Под шестерней

Моменты под шестерней определяются согласно формулам 10-12.

3. Суммарный момент

Суммарные моменты определяются согласно формулам 12-14.

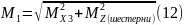
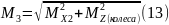
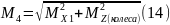
5. Расчёт подшипников

   1. Определение осевых сил, действующих на подшипник

Конструктивная особенность узлов с радиальными и радиально-упорными однорядными шарикоподшипниками такова, что внешнюю осевую нагрузку 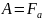воспринимает лишь одна опора. При этом следует учесть, что данные виды подшипников должны иметь осевой зазор близкий к нулю. Для удобства расчётов примем, что в рассчитываемой схеме нагружения осевой зазор шарикоподшипника равен нулю, в таком случае условие равновесия внутреннего кольца подшипника имеет вид:

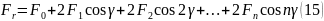
Где 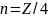для нулевого зазора, а 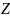– число тел качения. В этом случае будет нагружена половина тел качения и в точке контакта нагруженного тела с кольцом возникает осевая сила равная:

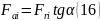
Где индекс «i» равен числу нагруженных тел качения, 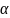– угол контакта.

Из формул 15 и 16 вытекает, что суммарная осевая нагрузка, обусловленная действием радиальной силы равна:

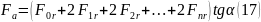
Исходя из схем нагружения (рис. 2) видно, что 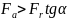, т.к. 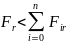. Поскольку угол и число тел качения являются стандартизованными величинами, получаем:

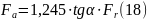
Рис.2. Схема распределения сил между телами качения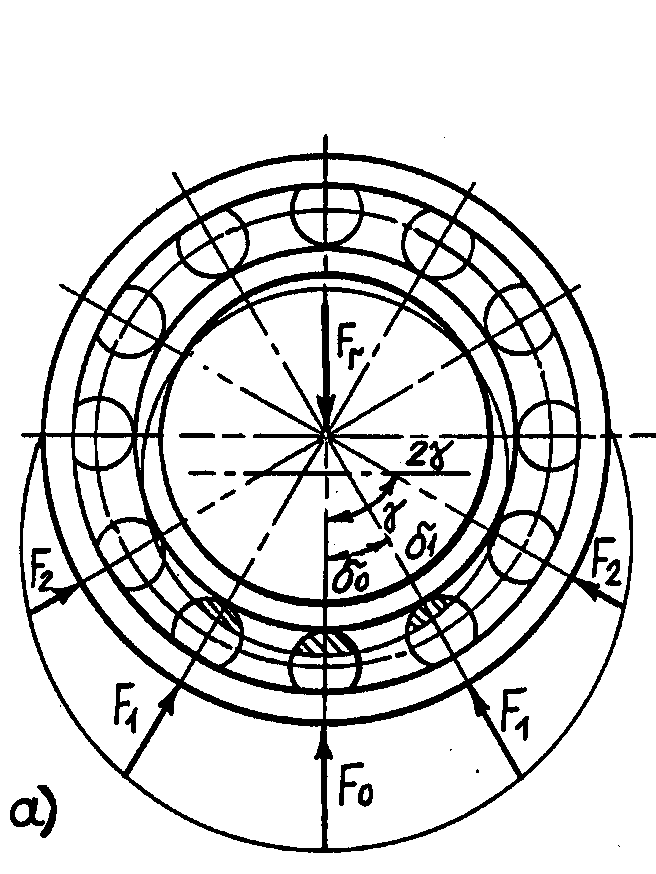

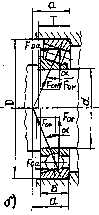
Обозначив множитель через e’, окончательно имеем:

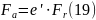
где e’= e – для радиально-упорного шарикоподшипника,

Величина e – параметр осевого нагружения, пропорциональный углу контакта . Таким образом, минимальная осевая сила, необходимая для регулируемого радиально-упорного подшипника, работающего с нулевым зазором при установившемся температурном режиме, равна

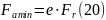
Особенности расчёта радиальных ( = 0) и радиально-упорных шарикоподшипников с углами контакта  = (1116) состоят в том, что для таких подшипников фактический угол контакта зависит от радиального зазора и деформаций, пропорциональных отношению Fа /Fr, и является переменной величиной.

Для радиальных шарикоподшипников (α = 0˚) при известном значении зависимость 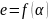можно представить в виде:

Где – статическая грузоподъёмность, находится из гостов.

Для радиально-упорных шарикоподшипников с углами контакта  = (11…16) и неизвестной 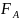предварительное значение e определяют по формуле:

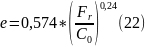
Затем после определения для обеих опор окончательное значение величины e находят таблицы 1.

Таблица 1.

Тип подшипника	Угол ,…	e	 е		 e
			X	Y	X	Y
Шариковый радиальный	0	0,518  0,19	1	0	0,56
Шариковый радиально-упорный	11…16	0,631  0,3	1	0	0,45
	18…20	0,57	1	0	0,43	1

Продолжение таблицы 1.

	24…26	0,68	1	0	0,41	0,87
	28…36	0,95	1	0	0,37	0,66
Роликовый радиально-упорный		1,5 tg 	1	0	0,40	0,4 ctg 