
Лабораторная №6 ИССЛЕДОВАНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНОВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
.docxЛАБОРАТОРНАЯ РАБОТА № 6
ИССЛЕДОВАНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНОВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Цель работы: изучение законов поступательно-вращательного движения твердого тела, сохранения энергии, определение момента инерции маятника.
Схема установки:
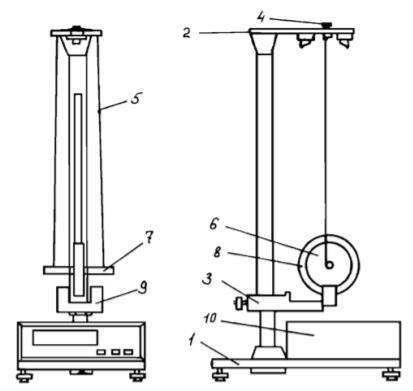
На вертикальной стойке 1 нанесена миллиметровая шкала, по которой определяется ход маятника. На нижнем кронштейне 3 находится фотоэлектрический датчик 9. Кронштейн обеспечивает возможность перемещения фотодатчика вдоль вертикальной стойки и его фиксирования в любом положении в пределах шкалы 0…420 мм. Фотодатчик предназначен для выдачи электрических сигналов на секундомер 10 в момент пересечения светового луча оси фотодатчика диском маятника.
Исследуемые закономерности:
Маятник
Максвелла поднят путём намотки нитей
на стержень имеет потенциальную энергию
равную
 ,
где
,
где
 – масса маятника,
– масса маятника,
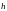 - высота подъёма маятника. Маятник
закрепляется электромагнитом. После
отключения электромагнита, нити начинают
раскручиваться и маятник совершает
поступательно-вращательное движение,
и потенциальная энергия переходит в
кинетическую энергию центра масс
маятника
- высота подъёма маятника. Маятник
закрепляется электромагнитом. После
отключения электромагнита, нити начинают
раскручиваться и маятник совершает
поступательно-вращательное движение,
и потенциальная энергия переходит в
кинетическую энергию центра масс
маятника
 и
энергию вращательного движения
и
энергию вращательного движения
 .
.
В момент полного разматывания нити происходит рывок маятника и частичный переход механической энергии в тепло. По закону сохранения энергии:
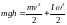
Так
как
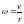 :
:
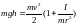 ,
где
,
где
 - скорость маятника в момент пересечения
оптической оси фотодатчика,
- скорость маятника в момент пересечения
оптической оси фотодатчика,
 - его угловая скорость вращения в тот
же момент времени,
- его угловая скорость вращения в тот
же момент времени,
 - радиус стержня, на который намотана
нить бифилярного подвеса маятника,
- радиус стержня, на который намотана
нить бифилярного подвеса маятника,
 -
момент инерции маятника.
-
момент инерции маятника.
Выведем формулу момента инерции:
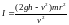
Так как:
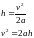
То момент инерции равен:

Так как:
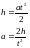
Тогда:
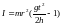
Если
учитывать теплоту
 ,
которая выделяется в момент рывка нити,
то закон сохранения энергии будет
выглядеть так:
,
которая выделяется в момент рывка нити,
то закон сохранения энергии будет
выглядеть так:
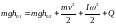 ,
где
,
где
 и
и
 отсчитываются в системе координат, ось
высот которой направлена вверх, а начало
находится в точке рывка нити.
отсчитываются в системе координат, ось
высот которой направлена вверх, а начало
находится в точке рывка нити.
Тогда
количество теплоты
,
которое выделится при рывке нити, можно
оценить по формуле
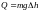 ,
где
,
где
 –
изменение высоты наивысшего положения
маятника.
–
изменение высоты наивысшего положения
маятника.
Теоретическое значение момента инерции маятника относительно его оси рассчитывается по формуле:
 ,
где
,
где
 -
масса стержня,
-
масса стержня,
 - масса диска, укрепленного на стержне,
- масса диска, укрепленного на стержне,
 - масса кольца,
- масса кольца,
-
радиус стержня,
 - внешний радиус диска,
- внешний радиус диска,
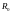 -
внешний радиус кольца.
-
внешний радиус кольца.
Контрольные вопросы:
№23
Как определяется работа при поступательном и вращательном движении?
При поступательном движении:
Работа
– скалярная
величина, характеризующая изменение
энергии, и равная произведению вектора
силы ![]() на
вектор перемещения
на
вектор перемещения ![]() .
.
Элементарная работа:

Интегральная работа:
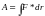
При вращательном движении:
Работа – скалярная величина, характеризующая изменение энергии, и равная произведению суммы моментов сил относительно оси вращения и угла поворота тела.
Элементарная работа:
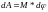
Интегральная работа:
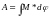
№14
Используя
теоретическое значение момента инерции
маятника
 ,
рассчитайте ускорение падения маятника.
,
рассчитайте ускорение падения маятника.
Дано:
= 0,029 кг
= 0,131 кг
= 0,312 кг
= 0,0045 м
= 0,045 м
= 0,0525 м
a=?
Решение:
Теоретическое значение момента инерции маятника относительно его оси рассчитывается по формуле:
 ,
где
-
масса стержня,
- масса диска, укрепленного на стержне,
- масса кольца,
,
где
-
масса стержня,
- масса диска, укрепленного на стержне,
- масса кольца,
- радиус стержня, - внешний радиус диска, - внешний радиус кольца.

Ответ: 0,105 м / с2
ИДЗ
№11
Напишите закон сохранения механической энергии для маятника в данной лабораторной работе. Объясните параметры, входящие в этот закон.
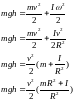
№5
Шар массой 2 кг катится без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара 15 см/с, после удара 10 см/с. Определить количество тепла, выделившегося при ударе.
Дано:
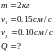
Решение:
Количество теплоты, которое выделится при ударе, равно изменению кинетической энергии шара:

Распишем кинетические энергии в двух случаях:

Тогда:
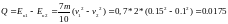
Ответ: 0.0175 Дж
Обработка результатов:
Проверим 1-ю выборку на наличие промахов:
Рассчитаем

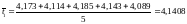
Рассчитаем
 :
:

Проверим на промахи:
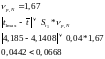

В первой выборке нет промахов.
Проверим 2-ю выборку на наличие промахов:
Рассчитаем
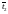 :
:

Рассчитаем
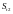 :
:
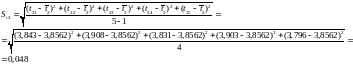
Проверим на промахи:
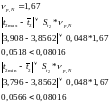
Во второй выборке нет промахов.
Проверим 3-ю выборку на наличие промахов:
Рассчитаем
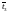 :
:

Рассчитаем
 :
:
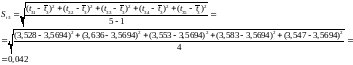
Проверим на промахи:
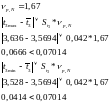
В третьей выборке нет промахов.
Проверим 4-ю выборку на наличие промахов:
Рассчитаем
 :
:

Рассчитаем
 :
:
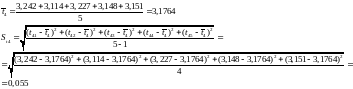
Проверим на промахи:

В четвёртой выборке нет промахов.
1.
Рассчитаем
 по формуле
по формуле
 .
Для
каждого
.
Для
каждого
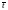
Для :
 м/с2
м/с2
Для :
 м/с2
м/с2
Для :
 м/с2
м/с2
Для :
 м/с2
м/с2
Для данной выборки:
Среднее значение:
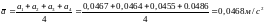
Рассчитаем СКО среднего:

Рассчитаем случайную и полную погрешность:
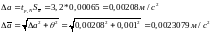
Тогда:

2.
Рассчитаем
по формуле
и
вычислим
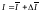

Посчитаем
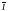 :
:

Рассчитаем СКО среднего:

Рассчитаем случайную и полную погрешность:
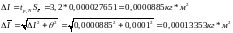
Тогда:

3.
Для одного из опытов рассчитаем величину момента инерции маятника по формуле:

4.
Рассчитаем теоретическое значение момента инерции маятника по формуле:
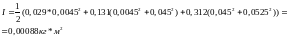
Значения различаются, так как мы не рассматриваем силу трения, которая действует на маятник.
Рассчитаем количество теплоты Q:
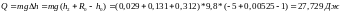
Вывод: изучил законы поступательно-вращательного движения твердого тела, сохранения энергии, определение момента инерции маятника.
