Назаренко София БСТ1904

Контрольные задания по дискретной математике

Часть 2

Вариант 14

Задание 1.

Формулировка задания:

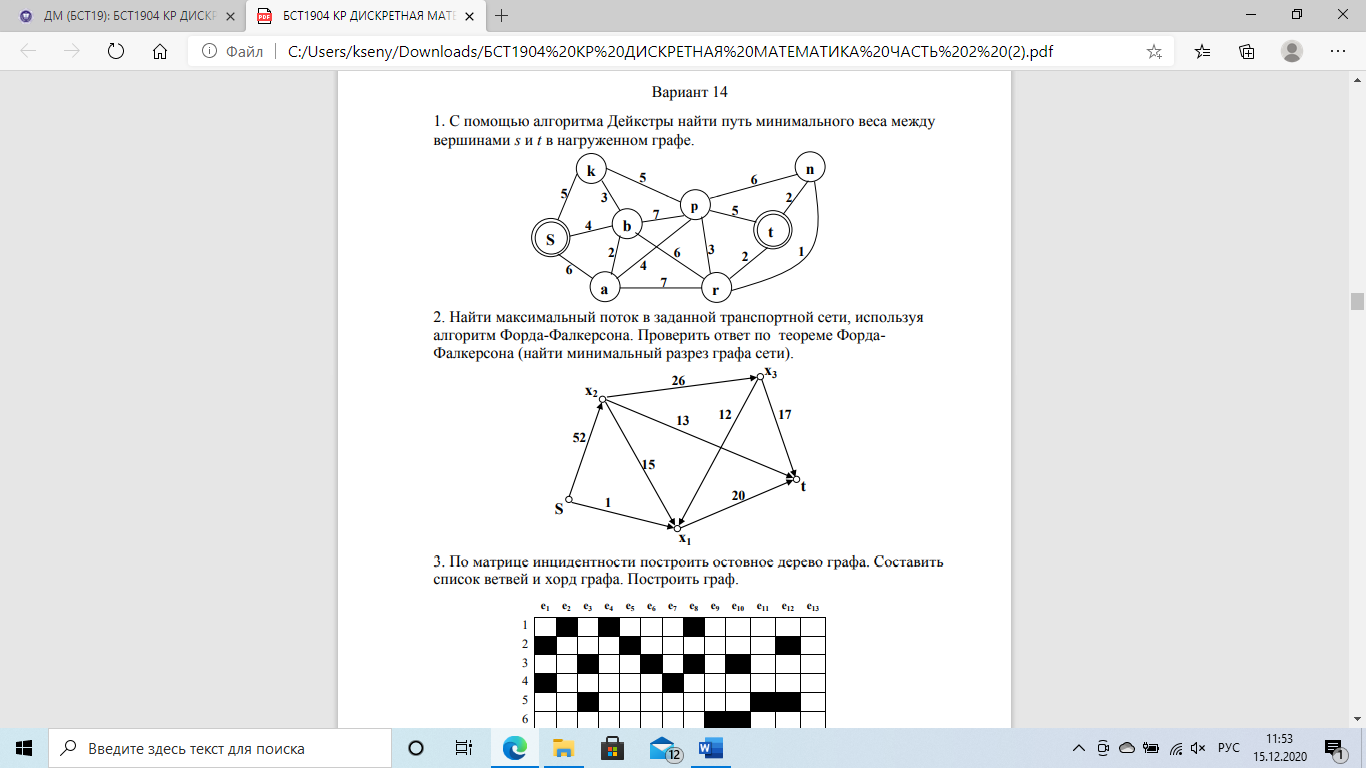
Полагаем: d(s)=0*; d(a)=d(b)=d(c)=d(р)=d(k)=d(n)=d(t)=∞.

1 итерация: текущая вершина с постоянной меткой y=s, далее расставляем

метки у вершин, достижимых из s

d(a)=6(s)

d(b)=4*(s)

d(k)=5(s)

d(p)= d(r)= d(n)= d(t)=∞

В скобках указана та вершина, через которую модифицируется метка рассматриваемой вершины (на первой итерации везде стоит вершина s). Звездочкой отмечена наименьшая метка из чисел 4, 5, 6. При этом данная метка будет постоянной (в нашем случае 4).

2 итерация: текущая вершина с постоянной меткой y=b, далее меняем метки у вершин с временными метками (меняются лишь метки тех вершин, которые достижимы из вершины y).

d(p)=min(∞,4+7)=11 (b)

d(a)= min(6,4+2) = 6 (s)

d(n)=d(t)=∞

d(k)= min(5,4+3)=5* (s)

d(r)= min(∞,4+6)=10 (b)

Метка (b), стоящая в скобке в строчке для d(p), означает, что путь из s в p,

проходящий через вершину d, короче пути, состоящего из одной дуги s-p. Аналогично в двух других случаях (5 строка).

3 итерация: текущая вершина с постоянной меткой y=k,

d(p)= min(11,5+5)=10 (k)

d(a)= min(6,4+2) = 6* (s)

d(n)=d(t)=∞

d(r)= min(∞,4+6)=10 (b)

4 итерация: текущая вершина с постоянной меткой y=a,

d(p)= min(10,6+4)=10* (k)

d(r)= min(10,7+6)=10 (b)

d(n)=d(t)=∞

Имеем 2 одинаковые метки с минимальным значением, поэтому выбираем

любую из них (в данном случае p).

5 итерация: текущая вершина с постоянной меткой y=p,

d(r)= min(10,10+3)=10* (b)

d(n)= min(∞,10+6)=16 (p)

d(t)= min (∞,10+5)=15 (p)

6 итерация: текущая вершина с постоянной меткой y=r,

d(n)= min(16,10+1)=11* (r)

d(t)= min (15,10+2)=12 (r)

7 итерация: текущая вершина с постоянной меткой y=n,

d(t)= min (12,11+2)=12* (r)

Вершина r имеет постоянную метку, и величина t имеет постоянную метку, следовательно 12 – длина кратчайшего пути от s до t. Сам путь находим по меткам, расставленным в скобках. А именно, вершине t предшествует r, что видно из 1 строки 7 итерации. Из 1 строки 5 итерации видим, что r предшествует b. Из 2 строки 1 итерации видим, что b предшествует s. Таким образом, имеем путь s-b-r-t. Видим, что его длина 12.

Задание 2.

Формулировка задания:

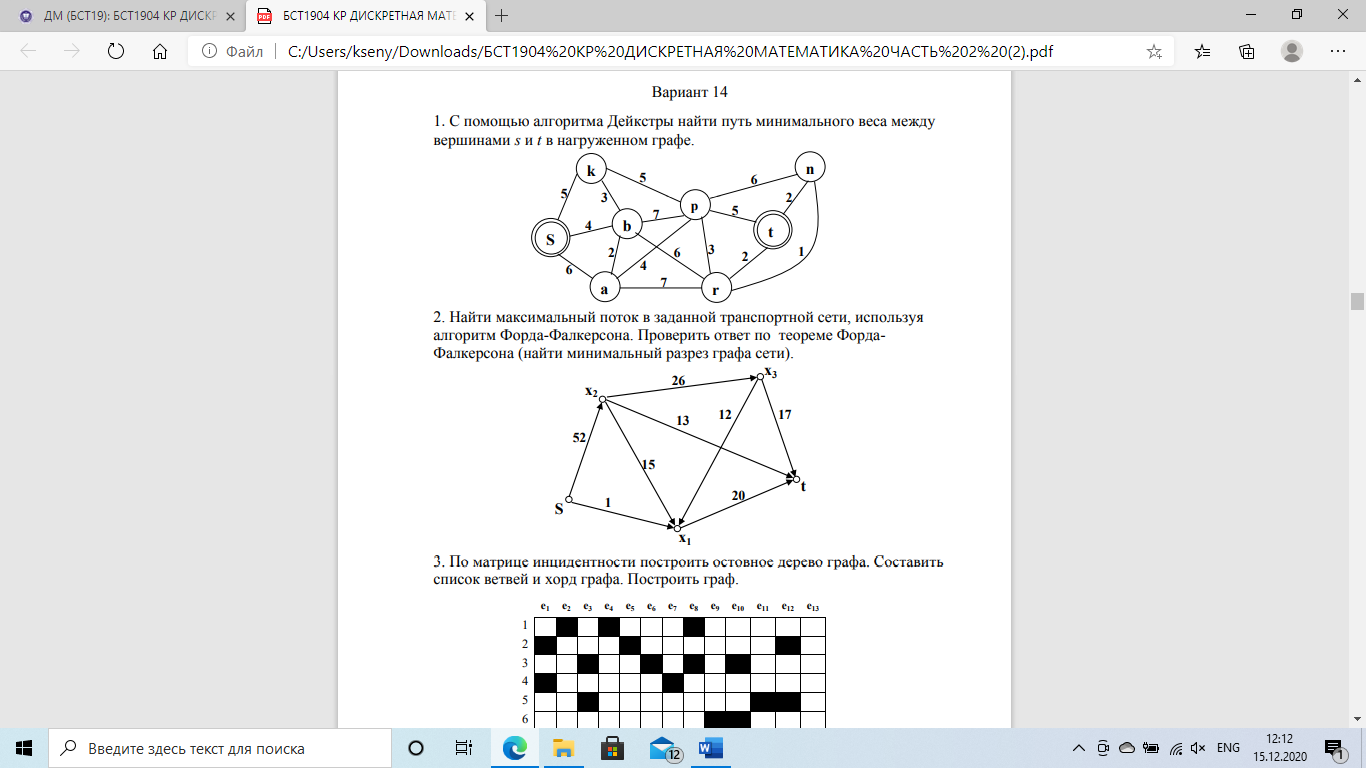
Составляем матрицу пропускных способностей:

	х1	х2	х3	t
S	1	52	0	0
x1	0	0	0	20
x2	15	0	26	13
x3	12	0	0	17

Находим путь из s в t как можно большей пропускной способности. Путь

максимальной пропускной способности можно найти с помощью алгоритма

волны, а для небольшой сети – визуально по графу.

Путь 1. s -> x2->x3->t. Пропускная способность: 17. Составляем матрицу

остаточных пропускных способностей/добавочного потока.

	х1	х2	х3	t
S	1	35/17	0	0
x1	0	0	0	20
x2	15	0	9/17	13
x3	12	0	0	0/17

Путь 2. s -> x2->x1->t. Пропускная способность: 15. Составляем матрицу

остаточных пропускных способностей/добавочного потока.

	х1	х2	х3	t
S	1	20/32	0	0
x1	0	0	0	5/15
x2	0/15	0	9/17	13
x3	12	0	0	0/17

Путь 3. s -> x2->t. Пропускная способность: 13. Составляем матрицу

остаточных пропускных способностей/добавочного потока.

	х1	х2	х3	t
S	1	7/45	0	0
x1	0	0	0	5/15
x2	0/15	0	9/17	0/13
x3	12	0	0	0/17

Путь 4. s -> x2->x3->x1->t. Пропускная способность: 5. Составляем матрицу

остаточных пропускных способностей/добавочного потока.

	х1	х2	х3	t
S	1	2/50	0	0
x1	0	0	0	0/20
x2	0/15	0	4/22	0/13
x3	7/5	0	0	0/17

Путь 5. Отсутствует. Алгоритм завершен.

Максимальный поток: П=П1+П2+П3+П4=17+15+13+5=50

Минимальный разрез: S->x1; x1->t; S->x2; x2->t; S->x2; x2->x3; x3->t. Пропускная способность данного разреза равна 50.

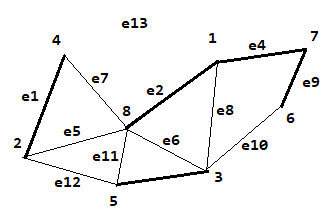
Задание 3.

Формулировка задания:

X{x1,x2,x3,x4,x5,x6,x7,x8}

1 итерация:

Шаг 1: X’{x2,x4}, X’’{x1,x3,x5,x6,x7,x8}, Г’={(x2,x4)}={e1}

Шаг 2: X’≠X, поэтому переходим на начало 1 шага

2 итерация:

Шаг 1: X’{ x1,x2,x4, x8}, X’’{x3,x5,x6,x7}, Г’={(x2,x4),(x1,x8)}={e1,e2}

Шаг 2: X’≠X, поэтому переходим на начало 1 шага

3 итерация:

Шаг 1: X’{ x1,x2, x3,x4,x5,x8 }, X’’{x6,x7}, Г’={(x2,x4),(x1,x8),(x3,x5)}={e1,e2,e3}

Шаг 2: X’≠X, поэтому переходим на начало 1 шага

4 итерация:

Шаг 1: X’{ x1,x2, x3,x4,x5,x7,x8 }, X’’{x6}, Г’={(x2,x4),(x1,x8),(x3,x5),(x1,x7)}={e1,e2,e3,e4}

Шаг 2: X’≠X, поэтому переходим на начало 1 шага

Далее ребра e5, e6, e7 и e8 не могут быть выбраны, так как их вершины

принадлежат множеству X’. Поэтому на следующей итерации выбираем ребро e9.

5 итерация:

Шаг1: X’{ x1,x2, x3,x4,x5,x6,x7,x8 }, X’’= , Г’={(x2,x4),(x1,x8),(x3,x5),(x1,x7),(x6,x7)}={e1,e2,e3,e4,e9}

Шаг 2: X’=X, конец работы алгоритма.

В результате получаем множество ветвей остова: Г’={(x2,x4),(x1,x8),(x3,x5),(x1,x7),(x6,x7)}={e1,e2,e3,e4,e9}

Соответственно множество хорд: Г\ Г’={e5,e6,e7,e8,e10,e11,e12,e13}

Строим граф. Жирным выделен остов.

Задание 4.

Формулировка задания:

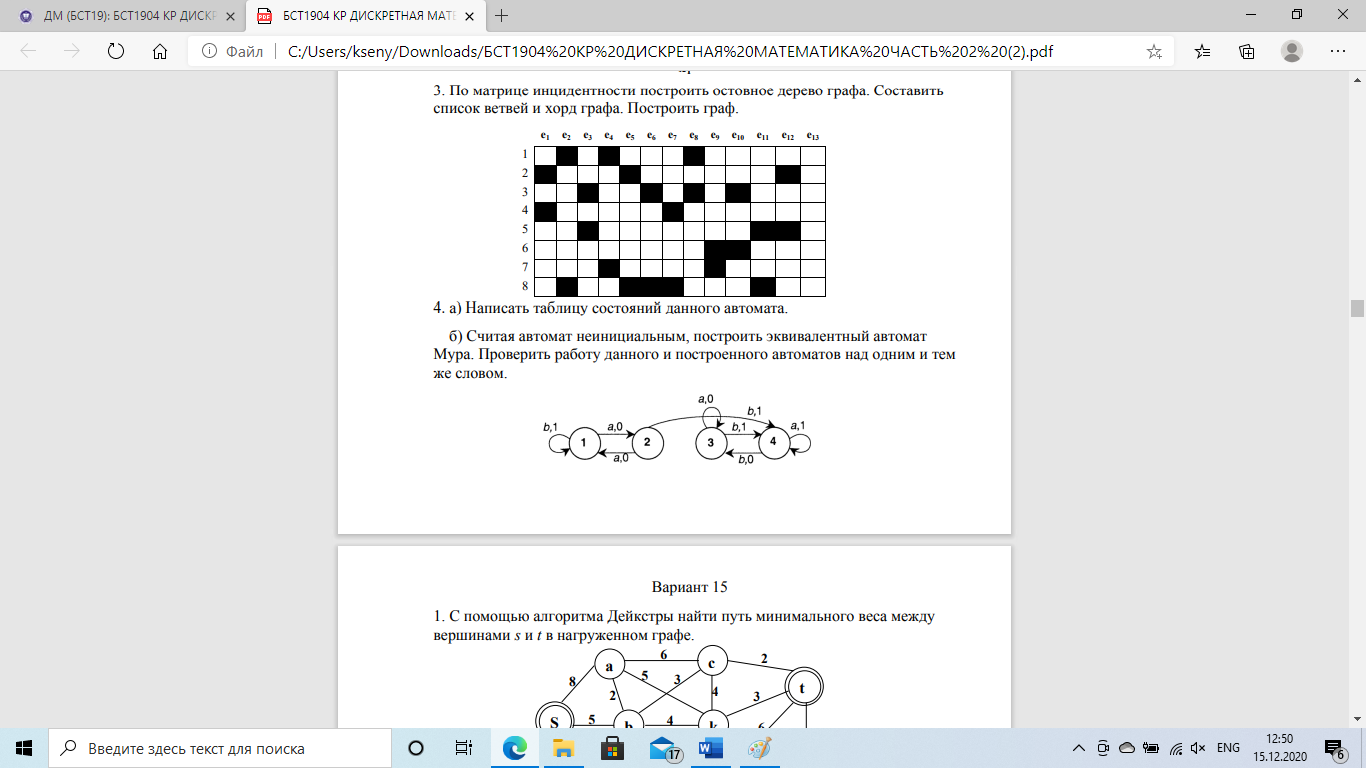
Изобразим таблицу данного автомата.

A Q	1	2	3	4
a	2,0	1,0	3,0	4,1
b	1,1	4,1	4,1	3,0

По данному неинициальному автомату Мили S строим эквивалентный ему автомат Мура S’ следующим образом:

Автомат S’ содержит 4*2+4=12 состояний, каждое из которых мы будем помечать двумя символами. Состояния автомата S’ обозначим так: *1, *2, *3, *4, a1, b1, a2, b2, a3, b3, a4, b4.

Функция отметок μ на состояниях *1, *2, *3, *4 не определена, а ее значения на состояниях a1, b1, …, b4 задаются с помощью функции выходов λ автомата S: 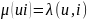, где 1≤i≤4, u⸦{a,b}. То есть μ(a1)=λ(a,1)=0, …, μ(b4)=λ(b,4)=1.

Функция переходов δ’ на состояниях, содержащих в изображении символ *, определяется так: δ’(u,*i)=ui, u⸦{a,b}, 1≤i≤4.

В остальных случаях первый символ имени нового состояния совпадает со считываемым символом входного автомата, а второй символ нового состояния определяется с помощью функции переходов δ автомата S: δ’(u,vi)=vi, где u,v⸦{a,b}, j=δ(v,i).

Получим: δ’(a,*1)=a1, δ’(b,a1)=b2, т.к. δ(a,1)=2, и т.д.

Запишем таблицу состояний полученного автомата Мура.

μ

-

-

-

-

0

1

0

1

0

1

1

0

A Q

*1

*2

*3

*4

a1

b1

a2

b2

a3

b3

a4

b4

a

a1

a2

a3

a4

a2

a1

a1

a4

a3

a4

a4

a3

b

b1

b2

b3

b4

b2

b1

b1

b4

b3

b4

b4

b3

Проверим работу исходного автомата над словом baaba, запустив его из 3 состояния:

	b	a	a	b	a
3	4	4	4	3	3
	1	1	1	0	0

Построенный автомат Мура запускаем из состояния *3:

	b	a	a	b	a
*3	b3	a4	a4	b4	a3
	1	1	1	0	0

Как видим, результаты обоих автоматов совпали.