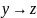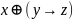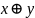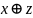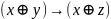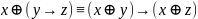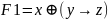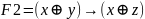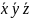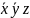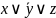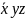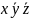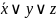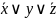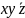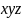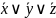ДМ КУРСАЧ Стас 22 В
.docxЗадание 1.
Формулировка задания:

а) Проверка по таблицы истинности
х |
y |
z |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
б) Метод алгебраических преобразований
Учитывая,
что

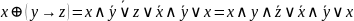

Формулы не эквивалентны
СДНФ и СКНФ построим с помощью таблицы истинности для левой(1) и правой(2) частью. Для наглядности при построении СДНФ используем двойственную функцию.
х |
y |
z |
|
|
Элементарные Конъюнкции функции 1 |
Элементарные Конъюнкции функции2 |
Элементарные Дизъюнкции функции 1 |
Элементарные Дизъюнкции функции2 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
0 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
0 |
0 |
0 |
1 |
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
1 |
1 |
1 |
0 |
1 |
|
|
|
|
Изобразим результат на кругах Эйлера:
Функция 1:
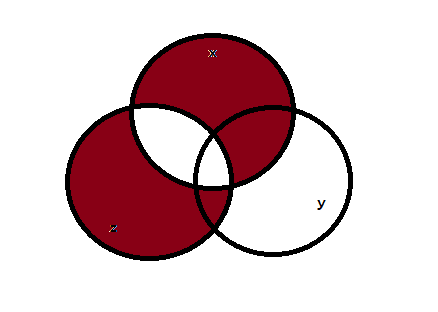
Функция 2:
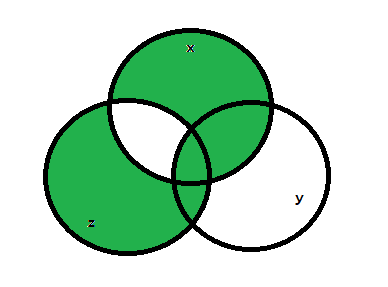
СДНФ:
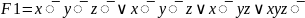
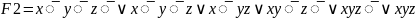
СКНФ:
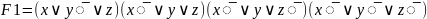

Функция 1.
х |
y |
z |
F |
Треугольник Паскаля |
Слагаемое |
||||||||
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
|
y |
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
|
|
yz |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
x |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
Получаем
многочлен Жегалкина:
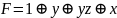
Функция 2.
х |
y |
z |
F |
Треугольник Паскаля |
Слагаемое |
||||||||
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
y |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
yz |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
xz |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
xy |
|
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
Получаем
многочлен Жегалкина:
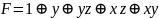
Задание 4.
Формулировка задания:

Изобразим таблицу данного автомата.
A Q |
1 |
2 |
3 |
4 |
a |
1,1 |
3,0 |
4,1 |
2,0 |
b |
2,0 |
4,0 |
3,0 |
1,1 |
По данному неинициальному автомату Мили S строим эквивалентный ему автомат Мура S’ следующим образом:
Автомат S’ содержит 4*2+4=12 состояний, каждое из которых мы будем помечать двумя символами. Состояния автомата S’ обозначим так: *1, *2, *3, *4, a1, b1, a2, b2, a3, b3, a4, b4.
Функция
отметок μ на состояниях
*1, *2, *3, *4 не определена, а ее значения на
состояниях a1, b1, …, b4 задаются с помощью
функции выходов λ автомата
S:
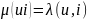 ,
где 1≤i≤4, u⸦{a,b}.
То есть μ(a1)=λ(a,1)=1,
…, μ(b4)=λ(b,4)=1.
,
где 1≤i≤4, u⸦{a,b}.
То есть μ(a1)=λ(a,1)=1,
…, μ(b4)=λ(b,4)=1.
Функция переходов δ’ на состояниях, содержащих в изображении символ *, определяется так: δ’(u,*i)=ui, u⸦{a,b}, 1≤i≤4.
В остальных случаях первый символ имени нового состояния совпадает со считываемым символом входного автомата, а второй символ нового состояния определяется с помощью функции переходов δ автомата S: δ’(u,vi)=vi, где u,v⸦{a,b}, j=δ(v,i).
Получим: δ’(a,*1)=a1, δ’(b,a1)=b1, т.к. δ(a,1)=1, и т.д.
Запишем таблицу состояний полученного автомата Мура.
μ |
- |
- |
- |
- |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
A Q |
*1 |
*2 |
*3 |
*4 |
a1 |
b1 |
a2 |
b2 |
a3 |
b3 |
a4 |
b4 |
a |
a1 |
a2 |
a3 |
a4 |
a1 |
a2 |
a3 |
a4 |
a4 |
a3 |
a2 |
a1 |
b |
b1 |
b2 |
b3 |
b4 |
b1 |
b2 |
b3 |
b4 |
b4 |
b3 |
b2 |
b1 |
Проверим работу исходного автомата над словом abaab, запустив его из 1 состояния:
|
a |
b |
a |
a |
b |
1 |
1 |
2 |
3 |
4 |
1 |
|
1 |
0 |
0 |
1 |
1 |
Построенный автомат Мура запускаем из состояния *1:
|
a |
b |
a |
a |
b |
*1 |
a1 |
b1 |
a2 |
a3 |
b4 |
|
1 |
0 |
0 |
1 |
1 |
Как видим, результаты обоих автоматов совпали.