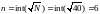- •Выборка случайных величин
- •По правилу разбиения интервала
- •По правилу разбиения интервала
- •Проверка соответствия выборочных данных по равномерному закону распределения по критерию
- •По правилу разбиения интервала или
- •По правилу разбиения интервала
- •По правилу разбиения интервала
- •Проверка соответствия выборочных данных по нормальному закону распределения по критерию
- •По правилу разбиения интервала или
- •По правилу разбиения интервала
- •По правилу разбиения интервала
- •Контрольные вопросы:
ФГБОУ ВО
«Уфимский государственный авиационный технический университет»
Кафедра ТК
ОТЧЕТ
по лабораторной работе № 1
по дисциплине «Моделирование»
по теме «Построение оценок законов распределения
случайной величины по выборочным данных»
Вариант 18
Выполнил: студент гр. ИВТ-225б
Колязов К.А.
Проверил:
Гвоздев В.Е.
Уфа 2022
Задача: по
выборочным данным проверить их
соответствие следующим законам
распределения (экспоненциальному,
равномерному, нормальному) по критериям
 и Колмагорова.
и Колмагорова.
Расчеты:
При использовании критерия проверка осуществляется для следующих правил разбиения интервала [xmin, xmax]:
Законы распределения:
Экспоненциальный
 ,
где
,
где ;
;
 .
.
Равномерный
 , где
, где
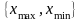 -наибольшее
и наименьшее из
-наибольшее
и наименьшее из
выборочных значений;

Нормальный
 ,
где
,
где

Расчеты границ интервалов группирования производятся по следующим формула:
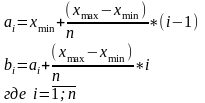
Вероятность попадания случайной величины определяется по правилу:
 ,
где
,
где
 - дифференциальная функция распределения;
F(x)
- интегральная функция распределения.
- дифференциальная функция распределения;
F(x)
- интегральная функция распределения.
Таблица 1
Выборка случайных величин
47 |
54 |
43 |
63 |
9 |
45 |
91 |
72 |
79 |
60 |
14 |
69 |
82 |
8 |
68 |
0 |
94 |
92 |
30 |
19 |
49 |
99 |
19 |
72 |
25 |
91 |
18 |
47 |
7 |
33 |
69 |
92 |
47 |
48 |
42 |
69 |
85 |
12 |
59 |
23 |
 =
0;
=
0;
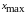 =
99.
=
99.
Проверка соответствия выборочных данных по экспоненциальному закону распределения по критерию

По правилу разбиения интервала
 или
или

Таблица 2
-
Номер интервала
mi
pi
Npi

1
6
0,3
10,50
1,926
2
7
0,2
7,67
0,059
3
8
0,1
5,61
1,022
4
4
0,1
4,10
0,002
5
8
0,1
3,00
8,364
6
7
0,1
2,19
10,574
 ;
;
 .
.
Сопоставив
 и
и
 можно заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
не согласуется с фактическими данным.
можно заключить, что гипотеза о том, что
выборочные данные соответствуют
экспоненциальному закону распределения,
не согласуется с фактическими данным.
По правилу разбиения интервала
Номер интервала |
mi |
pi |
Npi |
|
1 |
5 |
0,2 |
8,17 |
1,231 |
2 |
5 |
0,2 |
6,46 |
0,330 |
3 |
3 |
0,1 |
5,11 |
0,869 |
4 |
8 |
0,1 |
4,04 |
3,893 |
5 |
3 |
0,1 |
3,19 |
0,011 |
6 |
7 |
0,1 |
2,52 |
7,951 |
7 |
3 |
0,1 |
1,99 |
0,508 |
8 |
6 |
0,04 |
1,58 |
12,421 |
 ;
;
 .
.
Сопоставив и можно заключить, что гипотеза о том, что выборочные данные соответствуют экспоненциальному закону распределения, не согласуется с фактическими данным.
По правилу разбиения интервала
Таблица 4
-
Номер интервала
mi
pi
Npi
1
13
0,5
18,63
1,703
2
13
0,2
9,95
0,933
3
14
0,1
5,32
14,180
 ;
;
 .
.
Сопоставив и можно заключить, что гипотеза о том, что выборочные данные соответствуют экспоненциальному закону распределения, не согласуется с фактическими данным.