Ордена Трудового Красного Знамени

«Московский технический университет связи и информатики»

Кафедра ТЭЦ

Лабораторная работа №16

«Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре»

Выполнил: Студент группы БИН-2008 Ядринцев С.М.

Проверила: Степанова А.Г.

Москва 2021

Содержание

Содержание 2

Введение 3

Решение 4

Контрольные вопросы 15

Заключение 17

Введение

Цель: С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.

Задачи: Изучить основные положения теории цепей о резонансе напряжений стр. 84-97 [1], стр. 113-121 [2], стр. 4-18 [3], стр. 49-63 [4] и стр. 162-163, 168-170 [5]. Выполнить предварительный расчет, письменно ответить на вопросы для самопроверки.

Решение

Схемы

На рисунке 1 представлена схема цепи пассивного последовательного колебательного контура с сопротивлением R = 160 Ом

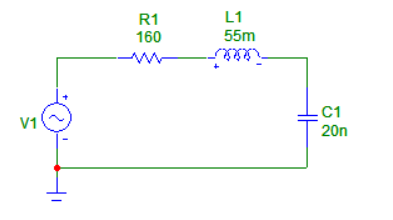
Рисунок 1 - Схема цепи пассивного последовательного колебательного контура с сопротивлением R = 160 Ом

На рисунке 2 представлена схема цепи пассивного последовательного колебательного контура с сопротивлением R = 640 Ом

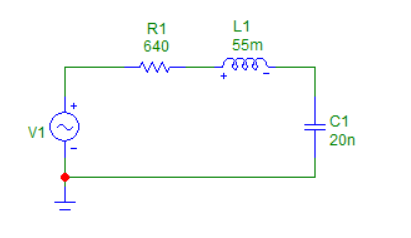
Рисунок 2 - Схема цепи пассивного последовательного колебательного контура с сопротивлением R = 640 Ом

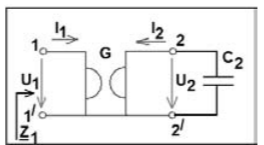
На рисунке 3 представлена схема активного колебательного контура с гиратором при сопротивлении R = 0,1 Ом.

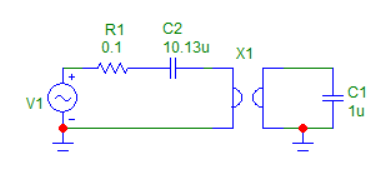
Рисунок 3 - Схема активного колебательного контура с гиратором при сопротивлении R = 0,1 Ом.

На рисунке 4 представлена схема активного колебательного контура с гиратором при сопротивлении R = 0,2 Ом.

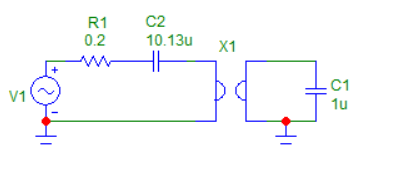
Рисунок 4 - Схема активного колебательного контура с гиратором при сопротивлении R = 0,2 Ом.

Расчётные формулы

Таблица

В таблице 1 представлены расчёты

По предварительному расчету U1=1 В, f0 = 4,8 кГц, C = 20 нФ, L = 55 мГн
R, ом	ρ, ом	Q	f1, Гц	f2, Гц	П, Гц	I0, мА	f0, кГц
160	1657,864	10,36	4573,962	3962,105	463,2467	6,25	4,8
640	1657,864	2,59	3962,105	5815,091	1852,987	1,56	4,8

Получено экспериментально
R, ом	f0, кГц	I0, мА	f1, Гц	f2, Гц	П, Гц	Q
160	4,8	6,25	4573	5036	463	10,36
640	4,8	1,56	3955	5823	1868	2,57

Гиратор
По предварительному расчету U1=1 В, f0 = 5 кГц, C1 = 1 мкФ, G = 0.1 Ом		Получено экспериментально
R, Ом	C2, мкФ		f0, кГц
0,1	10,13		5

Таблица 1. Расчёты

Графики

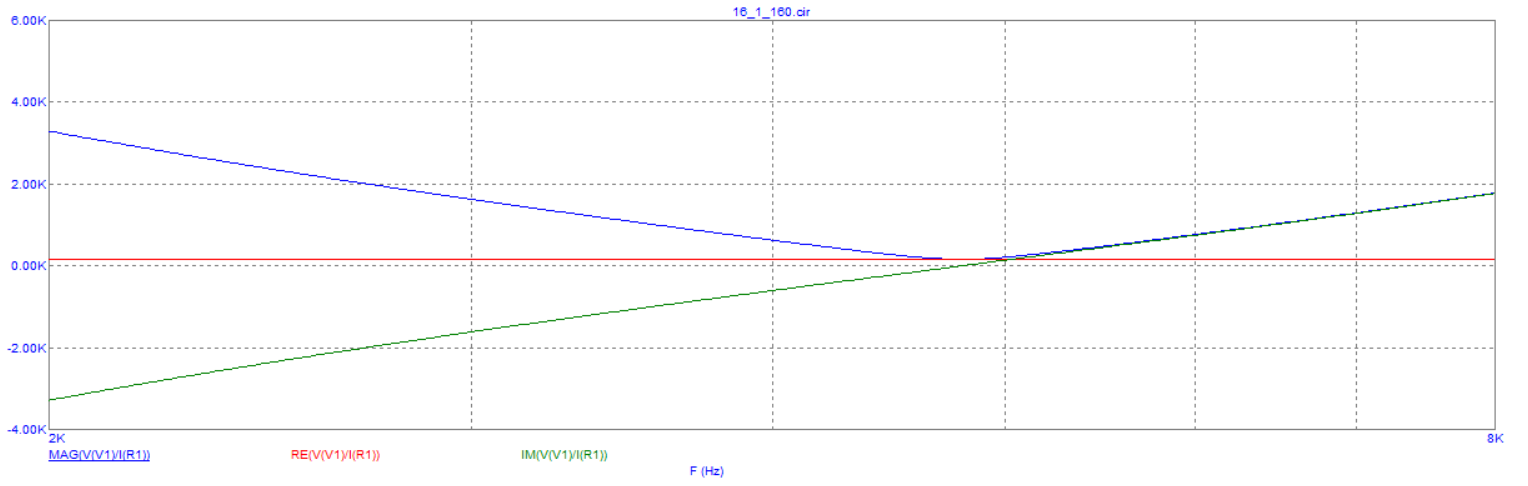
Рисунок 5 – графики зависимости входного сопротивления от частоты, действительной части входного сопротивления от частоты и мнимой части входного сопротивления от частоты.

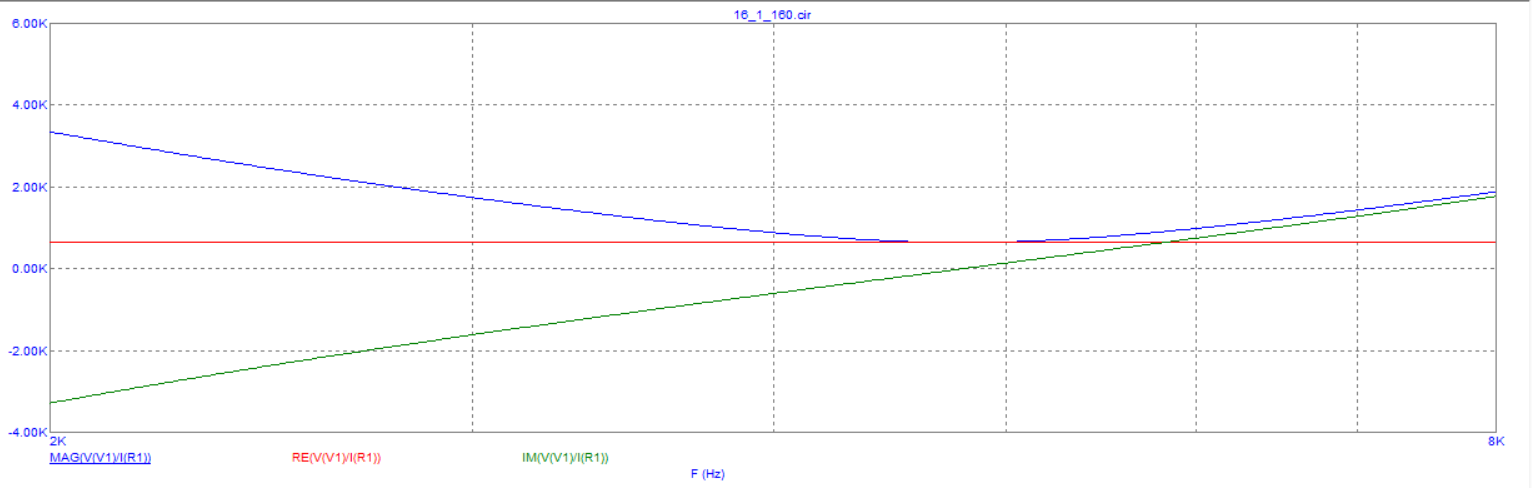
Рисунок 6 – графики зависимости входного сопротивления от частоты, действительной части входного сопротивления от частоты и мнимой части входного сопротивления от частоты.

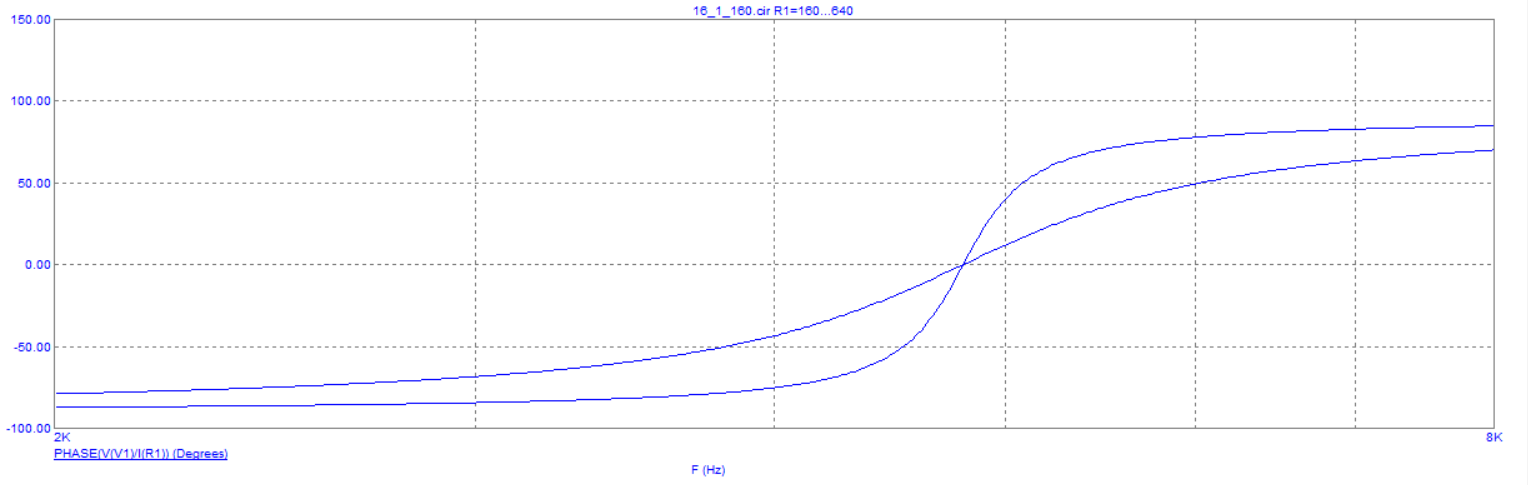
Рисунок 7 – графики зависимости фазы входного сопротивления от частоты при различных сопротивлениях.

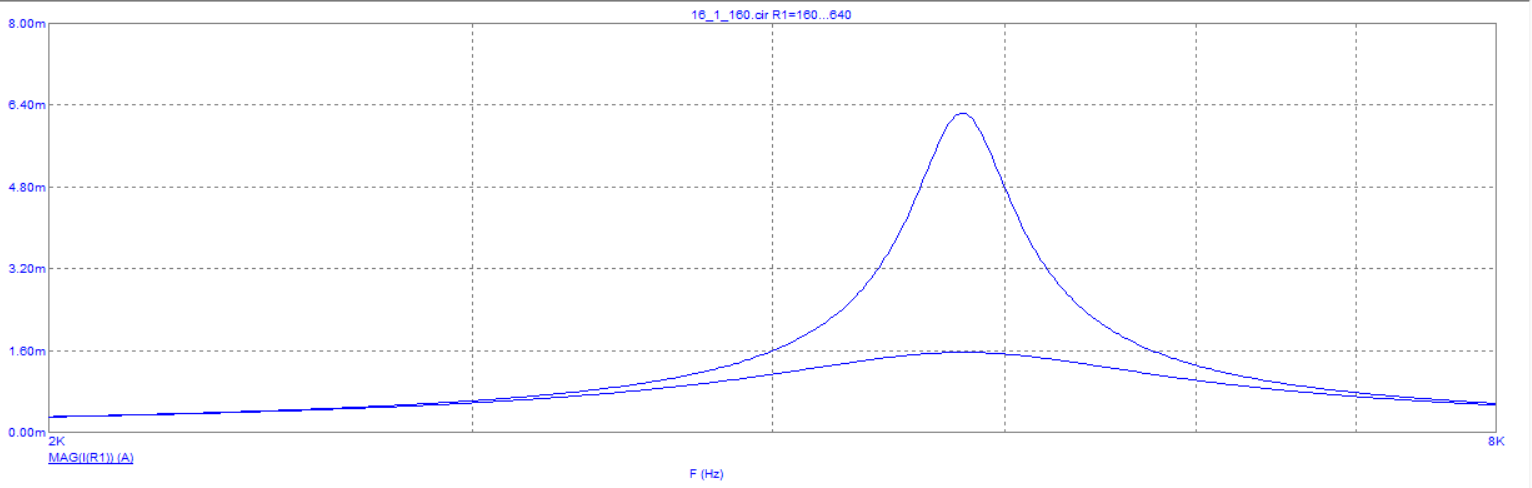
Рисунок 8 – графики зависимости модуля входного тока от частоты при различных сопротивлениях.

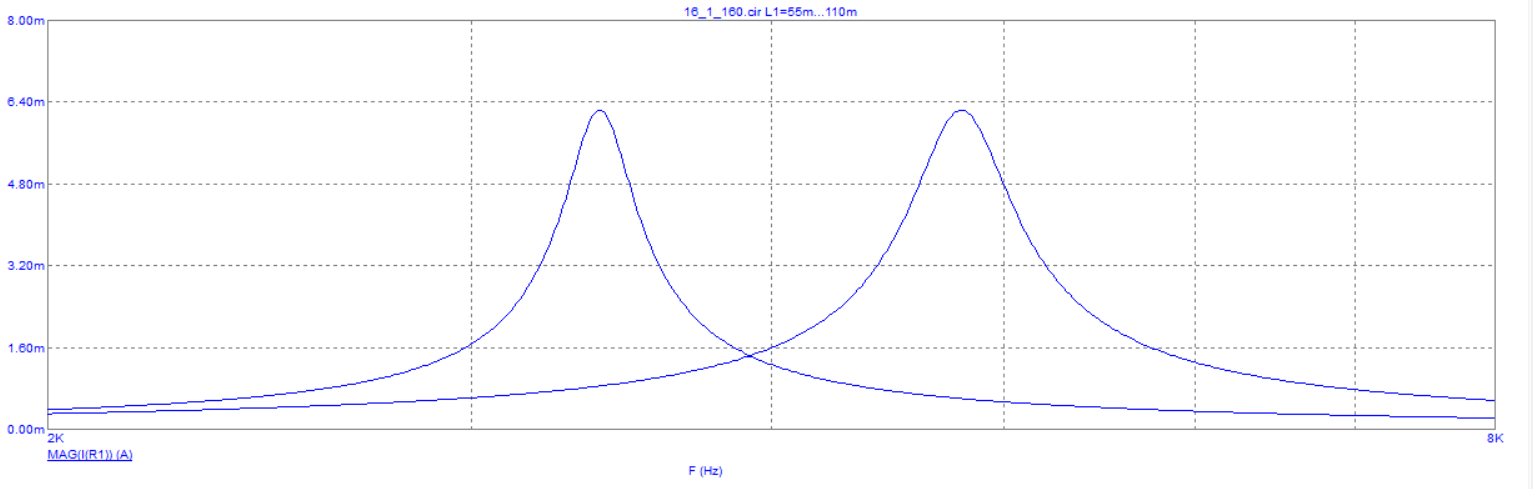
Рисунок 9 – графики зависимости модуля входного тока от частоты при различных значениях индуктивности.

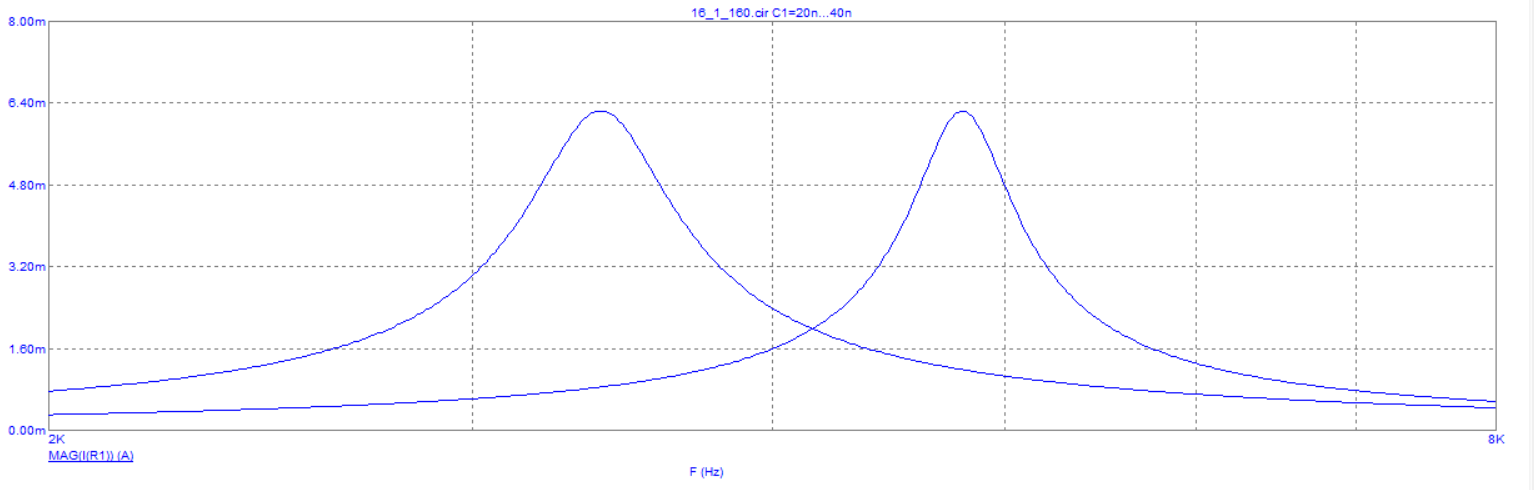
Рисунок 10 – графики зависимости модуля входного тока от частоты при различных значениях ёмкости.

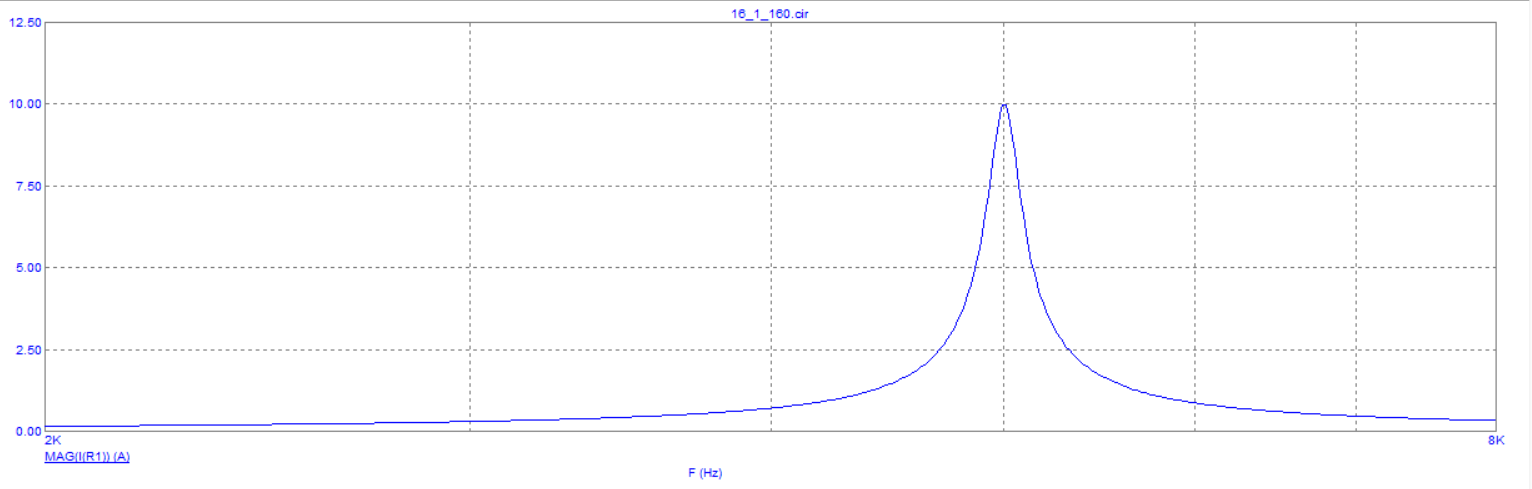
Рисунок 11 – график резонансной кривой при R = 0,1 Ом.

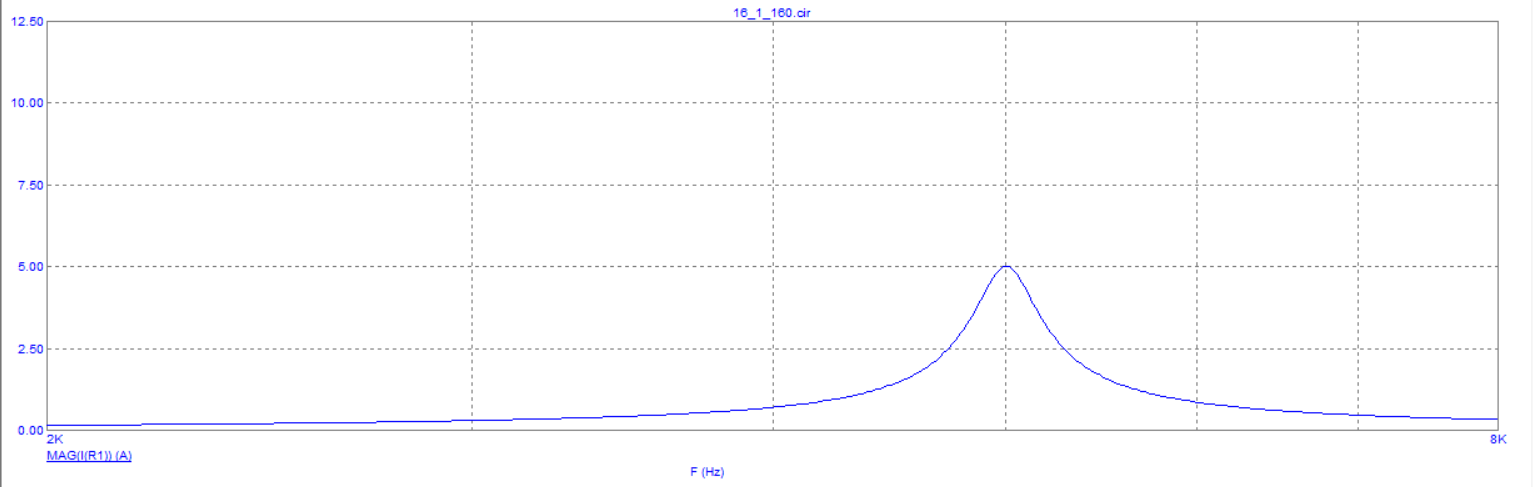
Рисунок 12 – график резонансной кривой при R = 0,2 Ом.

Контрольные вопросы

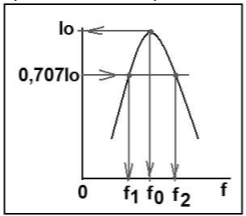
1. Почему резонанс в последовательном пассивном колебательном контуре называется резонансом напряжений?

Отношение волнового сопротивления к резистивному ρ/R = Q, называется добротностью контура. Таким образом, добротность равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Поэтому резонанс в последовательном контуре называется резонансом напряжений.

2. Как рассчитывается резонансная частота сложного пассивного колебательного контура и как она рассчитывается для схем, содержащих гиратор?

Для пассивного колебательного контура:

Для схемы, содержащей гиратор:

3. Что такое добротность последовательного пассивного колебательного контура?

Добротность колебательного контура - это величина, показывающая во сколько раз запасы энергии в контуре больше потерь энергии за один период колебаний.

4. Что такое полоса пропускания последовательного пассивного колебательного контура? Какие существуют способы расчета полосы пропускания?

Полоса пропускания последовательного пассивного колебательного контура – это диапазон частот, в пределах которого значение АЧХ составляет не менее, чем 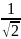от её максимального значения на резонансной частоте.

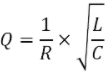
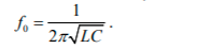
5. Выведите уравнения, с помощью которых рассчитывают входные АЧХ и ФЧХ последовательного пассивного колебательного контура.

Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.

Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:

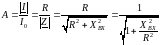Реактивное сопротивление контура равно:

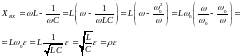
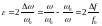- относительная расстройка контура

Тогда АЧХ:

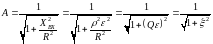
где 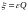- Обобщенная расстройка контура.

АЧХ:

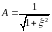
ФЧХ: :

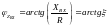
Заключение

Вывод: С помощью программы Micro-Cap исследованы характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.