Квазикристаллы

•Дан Ше́хтман (Daniel Shechtman, род. 24 января 1941, Тель- Авив) — израильский физик и химик, лауреат Нобелевской премии по химии за 2011 год «за открытие квазикристаллов»

•Квазикристаллы наблюдались впервые Даном Шехтманом в экспериментах по дифракции электронов на быстроохлаждённом сплаве Al6Mn

•Полученная картина дифракции содержала типичные для кристаллов резкие (Брэгговские) пики, но при этом в целом имела точечную симметрию икосаэдра, то есть, в частности, обладала осью симметрии пятого порядка, невозможной в трёхмерной периодической решётке.

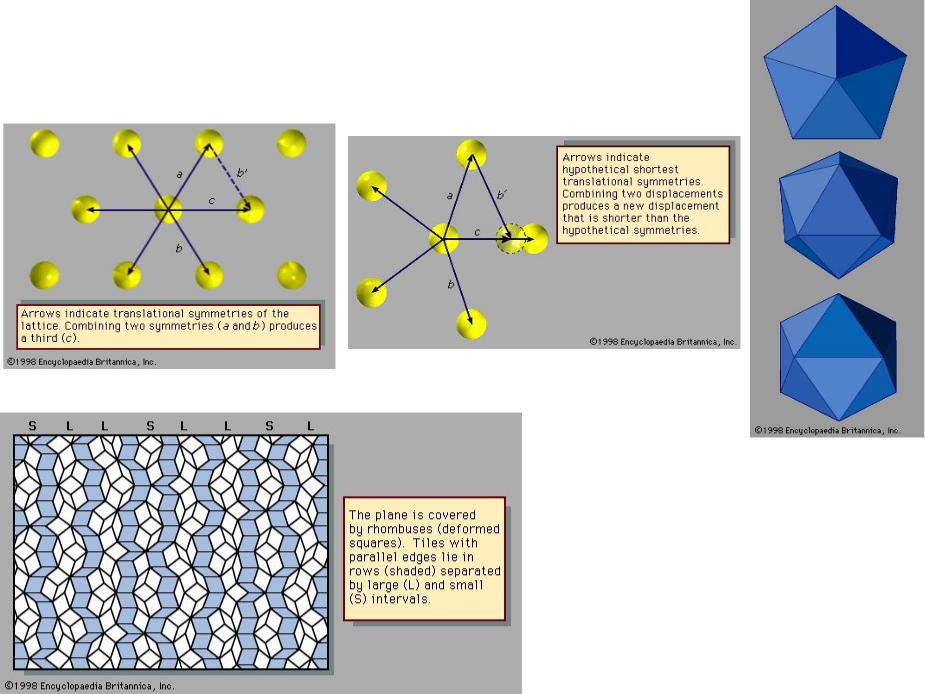
Квазикристаллы

Three views of the icosahedral symmetry of quasicrystalline aluminum-manganese. (Top) View is along the fivefold symmetry axis; (centre) rotating by 37.38° reveals the threefold axis, and (bottom) rotating by 58.29° reveals the twofold axis.

Обратная решетка

Возьмем множество точек R, составляющее решетку Браве, и плоскую волну eikr Множество волновых векторов K называют обратной

решеткой, если плоская волна с k K имеет периодичность данной решетки Браве.

Аналитически это означает, что для любого r и для всех R Браве справедливо равенство

Обратная решетка определена обязательно по отношению к некоторой конкретной решетке Браве.

Как выбрать вектора обратной решетки

Пусть a1, a2 , a3 вектора примитивных трансляций прямой решетки, тогда обратную решетку порождают следующие вектора:

числа. Тогда k R 2 k1n1 k2n2 k3n3 . Чтобы eiK R =1 для всех R произведение

k R должно быть равно целому числу, умноженному на 2 для любых ni. Это означает, что все ki должны быть целыми, а обратная решетка является решеткой Браве.

Обратная решетка. Продолжение

Решетка обратная к обратной

Обратная решетка является решеткой Браве, поэтому можно построить ее обратную решетку. Оказывается, она представляет собой просто исходную прямую решетку. Один из способов доказательства - построение векторов

c1, c2 , c3 из векторов b1, b2 , b3 . Видно, что они совпадают с векторами прямой решетки.

Объем элементарной ячейки обратной решетки

Если - объем элементарной ячейки прямой решетки, то элементарная ячейка обратной решетки имеет объем (2 )3/ .

Первая зона Бриллюэна

Ячейку Вигнера-Зейтца для обратной решетки называют первой зоной

Бриллюэна

Атомные плоскости и векторы обратной решетки

Атомная плоскость некоторой решетки Браве – любая из плоскостей, содержащих по меньшей мере три не лежащих на одной прямой точки этой решетки.

Семейство атомных плоскостей – множество параллельных равноотстоящих друг от друга атомных плоскостей, которые в совокупности содержат все точки трехмерной решетки Браве.

Обратная решетка позволяет очень просто классифицировать всевозможные семейства атомных плоскостей. Классификация основана на следующей теореме.

Теорема (примем без доказательства)

Для всякого семейства атомных плоскостей, отстоящих друг от друга на расстояние d, существуют такие векторы обратной решетки, которые перпендикулярны к этим атомным плоскостям, причем наименьший из них

имеет длину 2 /d. . Наоборот, для всякого вектора K обратной решетки существует семейство атомных плоскостей, которые перпендикулярны вектору

K и отстоят друг от друга на расстояние d, где 2 /d - наименьший вектор обратной решетки, параллельный K .

Индексы Миллера атомных плоскостей. Определение через векторы обратной решетки.

•Индексы Миллера некоторой атомной плоскости - это координаты наименьшего вектора обратной решетки, перпендикулярного данной плоскости, в системе координат, заданной основными векторами обратной решетки. Следовательно, плоскость, имеющая индексы Миллера h,k,l перпендикулярна вектору обратной решетки hb1+kb2+lb3.

•Определенные подобным образом индексы Миллера должны быть целыми числами и не могут иметь общего множителя.

•Для индексации плоскостей используют вектора обратной решетки, а для индексации направлений используют вектора прямой решетки.

•Плоскость (hkl) перпендикулярна вектору обратной решетки hb1+kb2+lb3., а направление [hkl] параллельно вектору прямой решетки ha1+ka2+la3

Формулировка Лауэ условия дифракции рентгеновских лучей на кристалле

Лауэ считал:

Кристалл состоит из тождественных микроскопических объектов, размещенных в узлах R решетки Браве

Каждый из узлов рассеивает падающее излучение во всех направлениях

Острые максимумы только в тех направлениях и для тех длин волн, для которых лучи, рассеянные всеми точками решетки, испытывают конструктивную интерференцию

Разность хода:

d cos + d cos =d (n-n )

Условие конструктивной интерференции