- •Свойства функций блоха.
- •Функции блоха.
- •Функции блоха.
- •Функции блоха.
- •Функции блоха.
- •Задача 1.
- •Решение
- •Решение
- •Решение
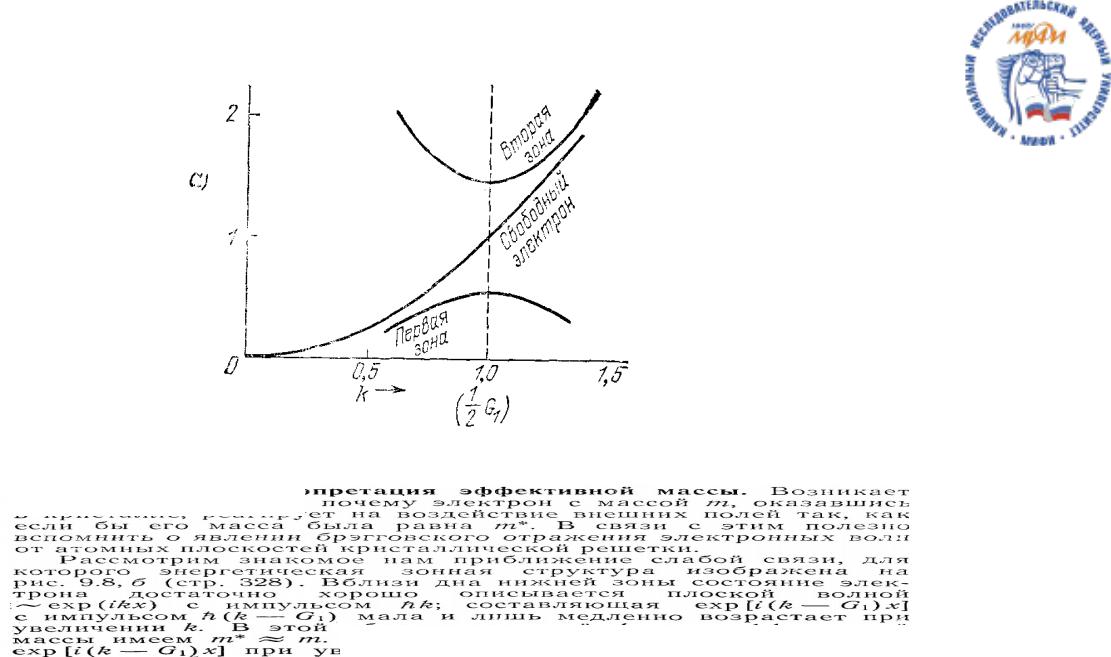
- •Параболоид энергий приведен к первой зоне Бриллюэна и раздвинут по вертикальной оси для
- •Физический смысл
- •Происхождение щели
- •Задача 2.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Задача 2.
- •Решение.
- •Решение.
- •Решение.
- •Физический смысл эффективной массы.

Решение.
Все приведенные графики относятся к случаю , поэтому по ним нельзя судить о влиянии проницаемости стенки на энергетический спектр. Для меньших значений правая часть неравенства будет быстрее приближаться к единице, и соответствующая кривая на рис. b будет пересекать косинусоиду в точках, более близких к максимумам последней. Это, разумеется, означает, что запрещенные зоны станут уже. Так как положения верхних границ разрешенных зон (точки ) не зависят от , то по мере уменьшения этой величины будут смещаться вниз на рис. b лишь одни нижние границы этих зон.
Зависимость энергии от переменной kа. Для трех первых зон (одномерные зоны Бриллюэна). Пунктирная кривая – парабола, отвечающая свободной частице.
Решение.
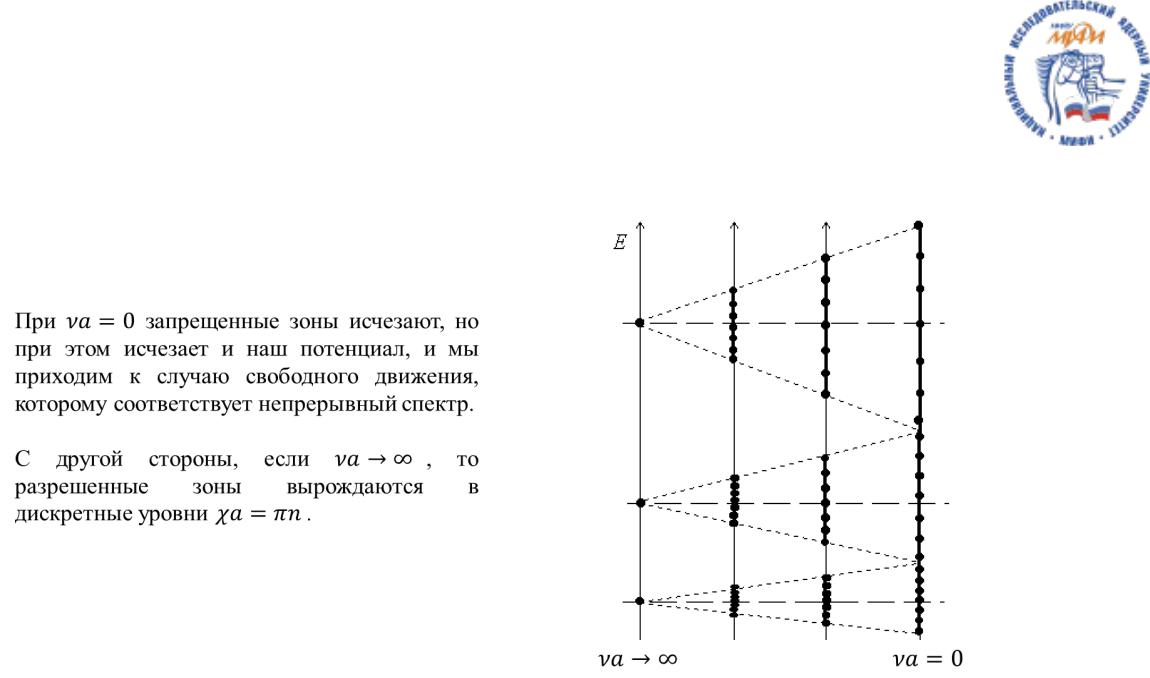
При запрещенные зоны исчезают, но при этом исчезает и наш потенциал, и мы приходим к случаю свободного движения, которому соответствует непрерывный спектр.
С другой стороны, если , то разрешенные зоны вырождаются в дискретные уровни .
→∞ |
=0 |

Решение.
Процесс возникновения широких энергетических зон в кристаллах можно понять, если представить, что имеется N атомов, которые расположены так же как в кристалле, но на значительном удалении друг от друга. Орбиты валентных электронов не возмущены. Тогда энергетический спектр этой системы из N атомов будет совпадать со спектром одного атома, только N-кратно вырожден. Если уменьшать расстояния между атомами, то взаимодействие между валентными электронами будет снимать вырождение уровней. Уровни будут расширяться и расщепляться. Это приводит к появлению зон.
→∞ |
=0 |
Решение.
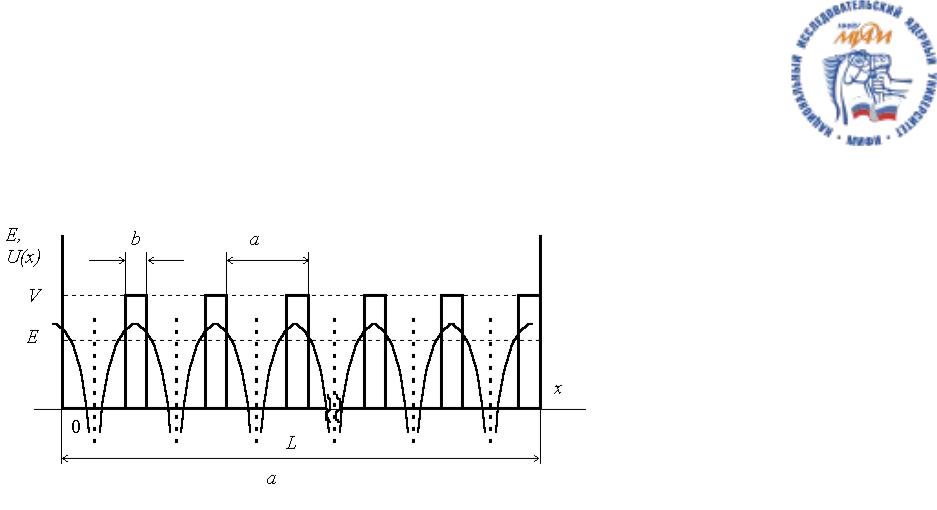
Изначально в модели Кронига-Пенни рассматривался потенциал, представляющий атомные остовы в виде бесконечной цепочки потенциальных ям прямоугольной формы. На ее основе можно получить качественно правильную картину энергетического спектра электронов в кристалле.

Задача 2.

Решение.

Решение.

Решение.

Физический смысл эффективной массы.