18. Смешанное произведение векторов: определение и приложения. «Элементы аналитической геометрии»

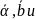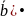
Рассмотрим произведение векторов , составленное следующим образом: ( 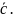Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Приложения смешанного произведения:

1. Определение взаимной ориентации векторов в пространстве

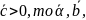
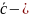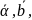
Определение взаимной ориентации векторов основано на следующих соображениях. Если правая тройка; если 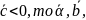– левая тройка.

2. Установление компланарности векторов

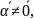
Векторы компланарны тогда и только тогда, когда их смешанное произведение равно нулю ( 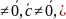(СМ. консп. По высш мат. 8.4)

19. Уравнения прямой на плоскости: с угловым коэффициентом и общее уравнение.

Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.

1. Уравнение прямой с угловым коэффициентом.

Под углом наклона прямой к оси 0х понимают угол, отсчитываемый в направлении движения, противоположном движению часовой стрелки, от положительного направления оси х до данной прямой.

Тангенс угла наклона прямой к оси 0х называется угловым коэффициентом этой прямой и обозначается k.

1. Если прямая ||оси 0х, то k = 0. Если прямая ⊥ оси 0х, то k не существует (обращается в ∝).

2. Если известен угловой коэффициент k и величина b отрезка, отсекаемого прямой на оси 0у, то как следует из рисунка, для произвольной точки М (х, у) этой прямой 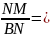tgα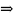 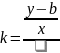. Откуда y = kx+ b =

уравнение прямой с угловым коэффициентом

Рис. См. « Лекции по ВМ соответственно»

Уравнение прямой с угловым коэффициентом:

Пусть: tg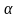 =k, 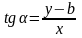, тогда: y = kx + b.

Число tg =k называется угловым коэффициентом прямой, а уравнение – уравнением прямой с угловым коэффициентом.

2. Уравнение прямой, проходящей через данную точку в данном направлении

Пусть прямая проходит через точку М(Хо,Уо) и ее направление характеризуется угловым коэффициентом к.

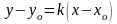
Уравнение с различными значениями к называют также уравнением пучка прямых с центром в точке М(Хо,Уо).

Обще уравнение прямой (см. §10.2 стр. 69)

Общее уравнение прямой в пространстве:

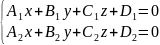
20. Уравнения прямой на плоскости: каноническое и параметрическое.

Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнений.

1. Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид:

.

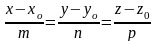где x0, y0, z0 - координаты точки, через которую проходит прямая, а m, n и p - направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой.

2. В параметрическом виде уравнения прямой линии в пространстве записываются так:

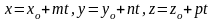
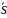(m,n,p) – направляющий вектор прямой (l), который параллелен этой прямой. M₀(x₀, y₀, z₀) ∈l.