кристаллы 12,16,22 вариант / ИПЗ 12 вариант

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ФХ

Отчёт

по практической работе №1

по дисциплине «Материаловедение»

Тема: Симметрия кристаллов

Студентка гр.
Преподаватель		Карпов О. Н.

Санкт-Петербург

2021

Цель работы:

Научиться качественно и количественно определять симметрию кристаллов на моделях, которые соответствуют формам реальных кристаллов минералов, металлов и других кристаллических веществ.

Вывод:

Мы изучили виды сингонии и классы симметрии кристаллов, научились искать центр симметрии, оси симметрии разных порядков и плоскости симметрии.

Литература:

1. Практическое руководство по геометрической кристаллографии. Нардов В. В. Учебное пособие. 1974. Изд-во Ленингр. ун-та, с. 3-142.

2. Кристаллография: учебное пособие к практическим занятиям по кристаллографии / Е.М. Нуриева, А.А. Ескин. – Казань: Казан. ун-т, 2017. – 94 с.

3. Симметрия кристаллов металлов и минералов: Лаб. практикум / Сост.: А.А. Пермяков: СибГИУ. - Новокузнецк, 2002. - 12с., табл.2, ил.7.

4. Занимательная кристаллография / Т.А. Еремина, Н.Н. Еремин. – М.: МЦНМО, 2014. – 149 с.

Ход выполнения работы

Вариант 12

Проекции к заданию 12-1 представлены на рисунке 1 «Проекции 12-1».

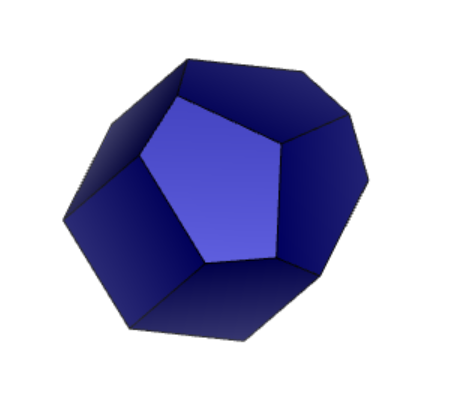
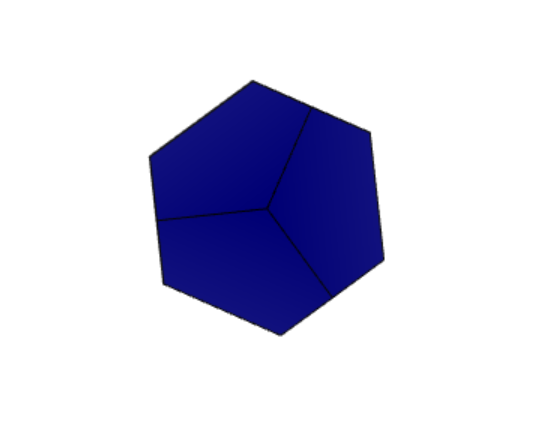
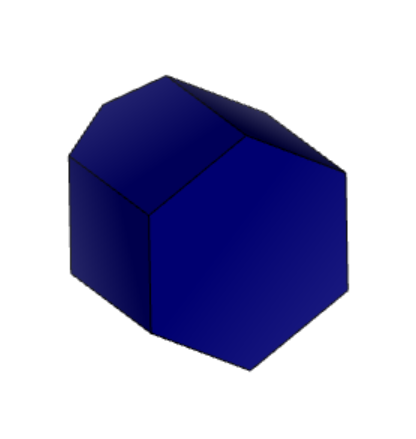
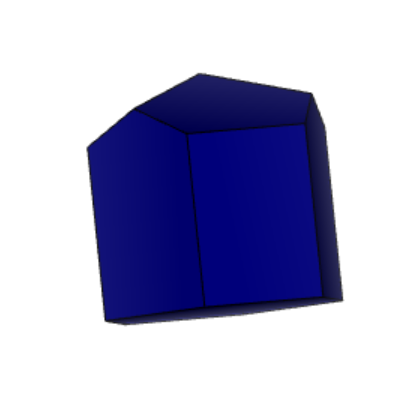
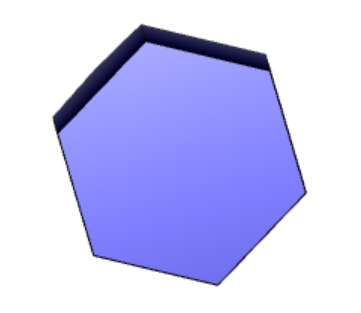
Рисунок 1 «Проекции 12-1»

Проекции к заданию 12-2 представлены на рисунке 2 «Проекции 12-2».

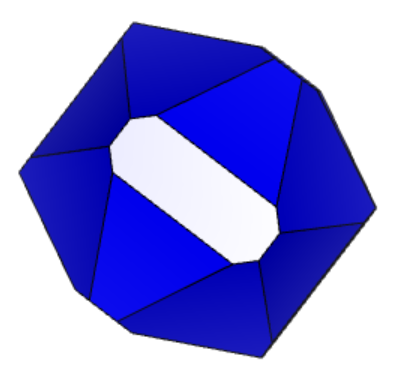
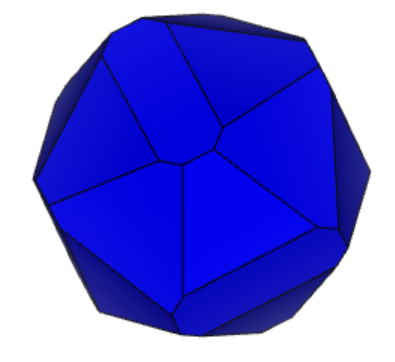
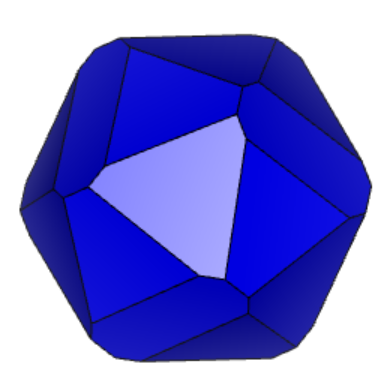
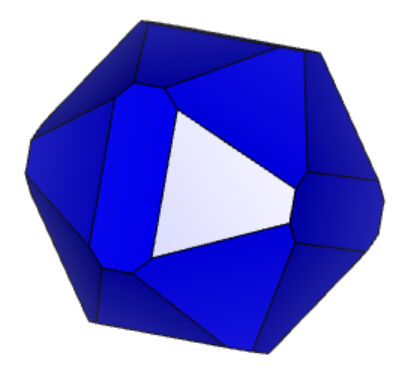
Рисунок 2 «Проекции 12-2»

Определяем симметрию кристаллов, найдя все возможные операции симметрии и заносим результаты в протокол.

Протокол

Номер варианта	Оси симметрии и их порядок				Плоскости Симметрии	Центр симметрии	Кристаллографичечкая формула	Сингония и вид (класс) симметрии
	2	3	4	6
12-1	-	1	-	-	3	-	L33P	Тригональная, планальный
12-2	3	4	-	-	3	1	4L33L23PC	Кубический, центральный

Таблица 1 «Протокол»

Найдём центр симметрии у кристаллов 12-1 и 12-2. Результат представлен на рисунке 3 «Результат поворота вдоль осей 12-1».

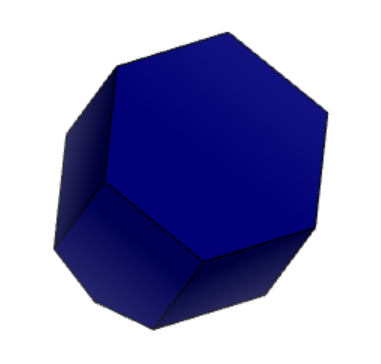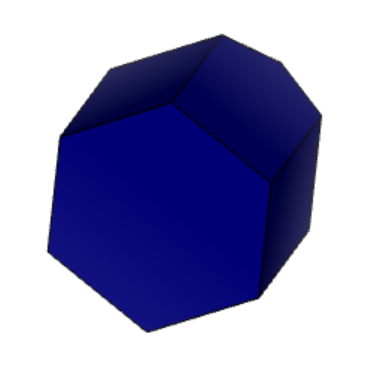1. 2. 3.

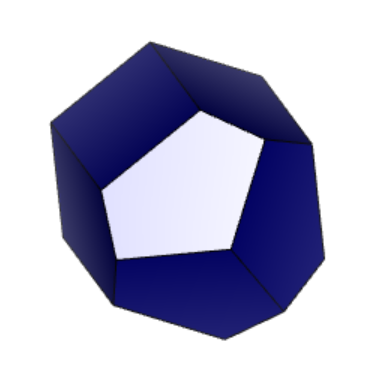
Рисунок 3 «Результат поворота вдоль осей 12-1» 1) – X, 2) – Y, 3) - Z

Из представленного выше, можно сделать вывод, что фигура не имеет центра симметрии так как при повороте вдоль осей X, Y, Z форма подсвеченной грани сохраняется только для одного случая. В таком случае остальные грани можно не проверять.

Проделаем тоже самое для кристалла 12-2 (см. рисунок 4.1 и 4.2 «Результат поворота вдоль осей 12-2».

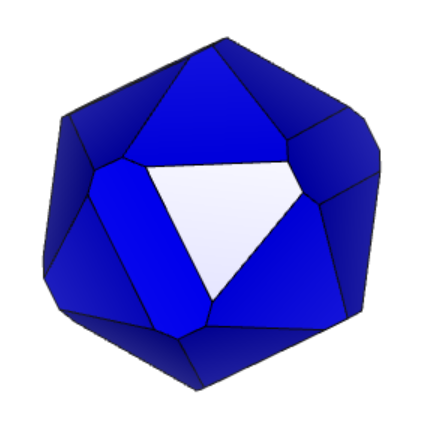
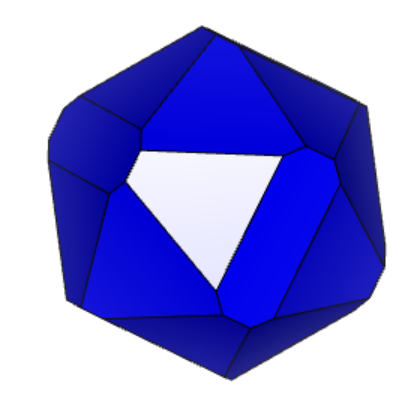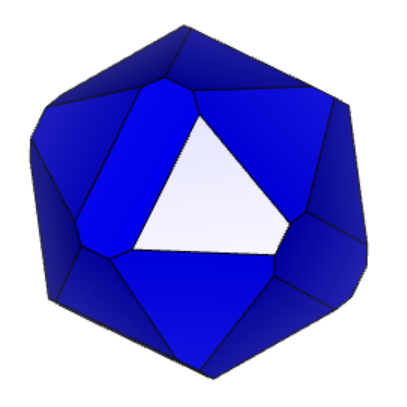1. 2. 3.

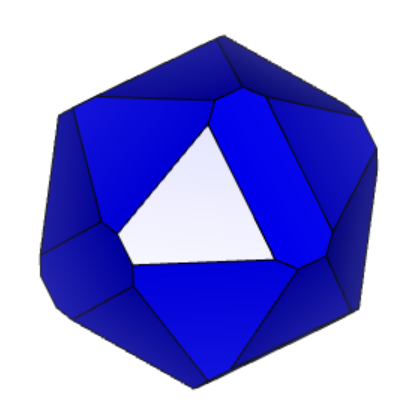
Рисунок 4.1 «Результат поворота вдоль осей 12-2» 1) – X, 2) – Y, 3) - Z

Из представленного выше, мы видим, что форма подсвеченной грани сохраняется при повороте вдоль осей X, Y, Z. Аналогично проверим остальные грани.

1 2 3

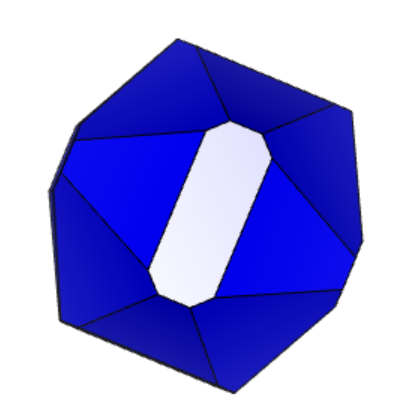
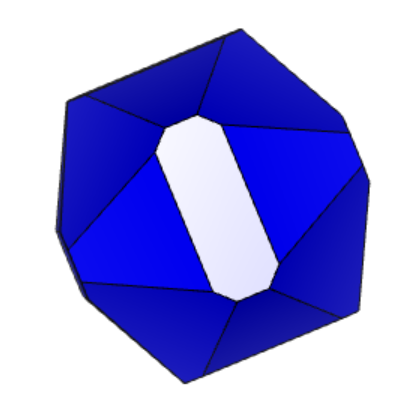
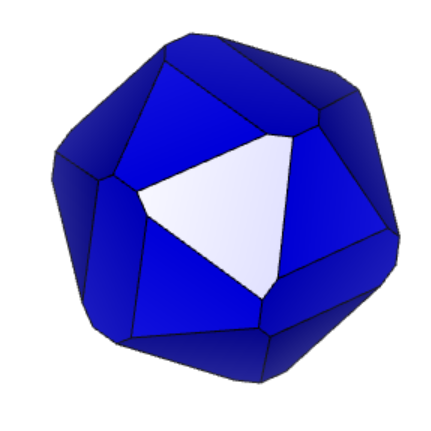
Рисунок 4.2 «Результат поворота вдоль осей 12-2» 1) – X, 2) – Y, 3) – Z

Таким образом, в фигуре 12-2 можно выделить три грани разной формы. Мы проверили каждую из трех граней на поворот вдоль осей X, Y, Z. Так как форма подсвеченной грани сохранилась, модель кристалла содержит центр симметрии.

Вид сверху на кристалл 12-1 (см. рисунок 5 «Вид сверху 12-1»). Применим операцию поворота вдоль оси на 120 градусов и убедимся, что фигура совмещается сама с собой.

1)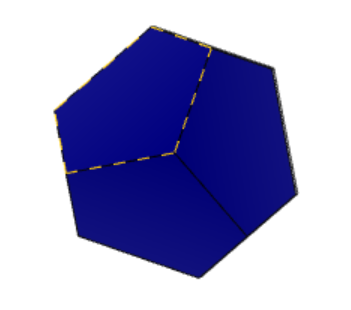 2)

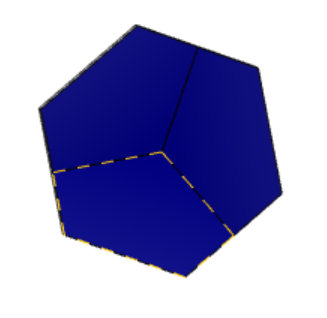
Рисунок 5 «Вид сверху 12-1»

1) исходное состояние 2) поворот на 120 градусов

Таким образом, у данной фигуры ось симметрии 3-его порядка, так как при повороте на 120 градусов фигура совместилась сама с собой.

Вид сверху на кристалл 12-2 (см. рисунок 6 «Вид сверху 12-2»). Проверим его на наличие осей симметрии.

1) 2)

3) 4)

Рисунок 6 «Вид сверху 12-2»

1) исходное состояние 2) поворот на 120 градусов

3) исходное состояние 4) поворот на 180 градусов

Таким образом, у кристалла 12-2 4 оси 3-его порядка и 3 оси 2-ого порядка.

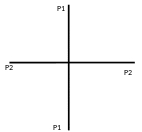
Плоскость симметрии делит фигуру на две зеркально равные части. Демонстрации плоскости симметрии кристалла 12-1 представлена на рисунке 7 «Плоскости симметрии 12-1». Таким образом, данный кристалл имеет три плоскости.

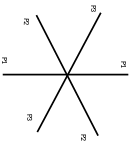
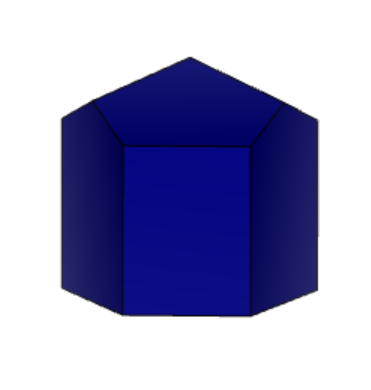
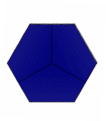
Рисунок 7 «Плоскости симметрии 12-1»

Плоскости симметрии у кристалла 12-2 рассмотрены на рисунке 8 «Плоскости симметрии 12-2».

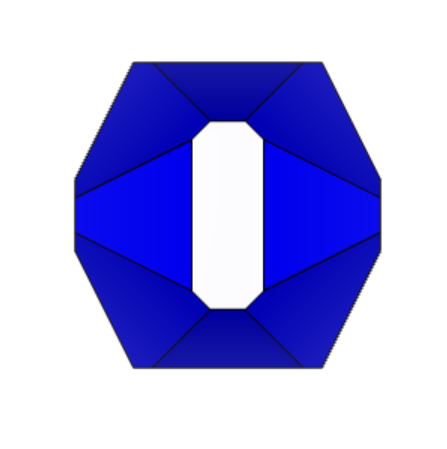
Рисунок 8 «Плоскости симметрии 12-2»

Таким образом, у кристалла 12-2 три плоскости симметрии, две из которых показано на рисунке, а третья идёт параллельно экрану, поэтому показать её невозможно.

Обработка данных

1. Мы записали в протоколе кристаллографическую формулу кристалла согласно символике Браве. (см. Таблицу 1 «Протокол»)

2. По полученной формуле кристалла с помощью таблицы определили, и записали, к какому виду сингонии и категории относится данный кристалл.

Привели примеры минерала для каждой модели кристалла по найденной формуле кристалла (см. рисунок 9 и 10). Пример для кристалла 12-1 приведён на рисунке 9 «Турмалин». Пример для кристалла 12-2 приведён на рисунке 10 «Сперрилит».

Рисунок 9 «Турмалин»

Рисунок 10 «Сперрилит»

3. Сосчитаем количество вершин (В), ребер (Р) и граней (Г).

12-1: В = 16, Р = 24, Г = 10. В – Р + Г = 16–24 +10 = 2

12-2: В = 48, Р = 72, Г = 26. В – Р + Г = 48–72+26 = 2

Вывод:

Таким образом кристалл 12-1 и 12-2 соответствует теореме Эйлера для многогранников.