3. Эдс от высших гармоник магнитного поля. Улучшение формы кривой эдс.

Ну что ж, пездос то только начался))). Теперь то же самое, только для высших гармоник, то есть ν (частота, а не скорость) = 3, 5, 7, 9, 11 и т.д. (ведь гармоники только нечётные). Советую посмотреть самый первый рисунок в прошлом вопросе.

У нас появляется новое полюсное деление для ν-ой гармоники: Потому что в одном реальном полюсном делении помещается целых ν полупериодов магнитной индукции.

Из-за высших гармоник магнитной индукции появляются высшие гармоники ЭДС.

При укорочении шага у нас появляется сдвиг проводников уже не βπ, а νβπ.

Поэтому везде, где до этого в различных формулах присутствовало выражение βπ, его надо заменить на νβπ (то есть в коэффициенте укорочения шага обмотки). Формула выше.

Изменится поток для ν-ой гармоники, потому что изменилось полюсное деление.

Также изменится сдвиг фаз ЭДС соседних катушек (было α и αq, а станет να и ναq), поэтому изменится и коэффициент распределения. Формула выше с опечаткой, вот правильная .

И аналогично изменится и угол скоса паза относительно поля ν-ой гармоники (был γ_с, стал νγ_с). И изменится коэффициент скоса. Здесь формула выше, но там опечатка, и там в числителе должен быть синус от всего того, что написано в числителе, знаменатель правильный.

Ну и полная ЭДС ν-ой гармоники считается по формуле в красной рамке. Если ЭДС различных гармоник имеют различные частоты, то полная ЭДС обмотки считается по формуле через корень из суммы квадратов.

А теперь погнали улучшать форму кривой ЭДС, ведь она там вся побитая вообще.

ЭДС от 3й гармоники поля. (я считаю это нелегальным физическим волшебством, потому что убираются все гармоники, кратные 3м, а это просто ДАХУИЩА)

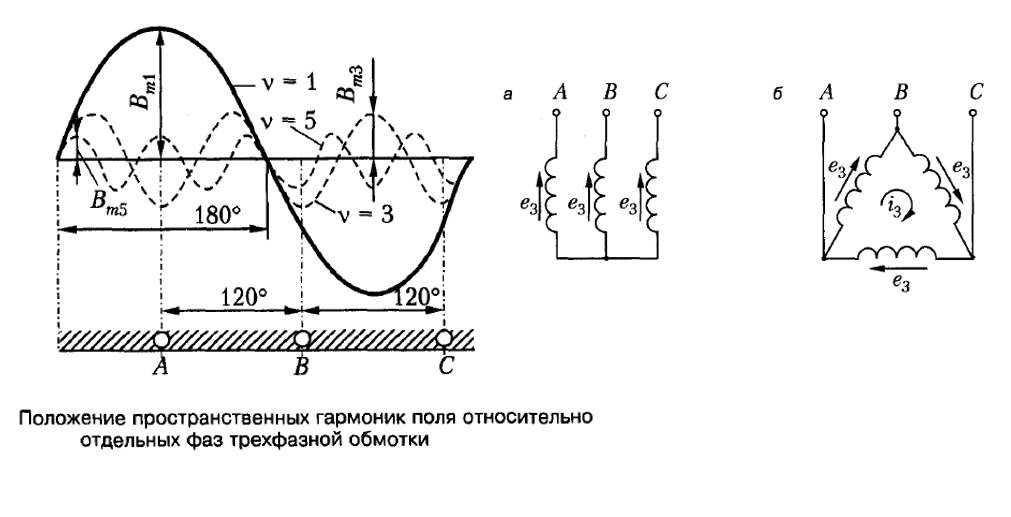
Имеем фазы A, B, C. Если фазы сдвинуты на 120 градусов, то для них всех фазы индукции совпадают (смотрите на рисунок, откуда идут пунктиры из А, В, С и на кривую B_m3). Точно так же совпадут и фазы ЭДС (ещё из трансформаторов знаем).

Если обмотка статора соединена звездой, то в линейных напряжениях ЭДС третьей гармоники не будет, потому что совпадает модуль и фаза фазного ЭДС.

Если обмотка статора соединена в треугольник, то у нас уже есть линейное ЭДС. Но у нас образуется замкнутый контур, по которому будет течь ток I₃ из-за этих ЭДС. Этот ток (пиздец какой волшебный) вызывает такое дополнительное падение напряжения, что оно компенсирует действие ЭДС. И суммарно линейное напряжение получается близким к нулю. Но возникают тепловые потери, поэтому обычно статор в треугольник не соединяют.

Что можно сделать теперь с ещё более высшими гармониками (5, 7 и т.д.). Попробуем укоротить шаг обмотки (вот тут уже, объективно, красивый подгон под ответ на основании того, как работает укорочение шага).

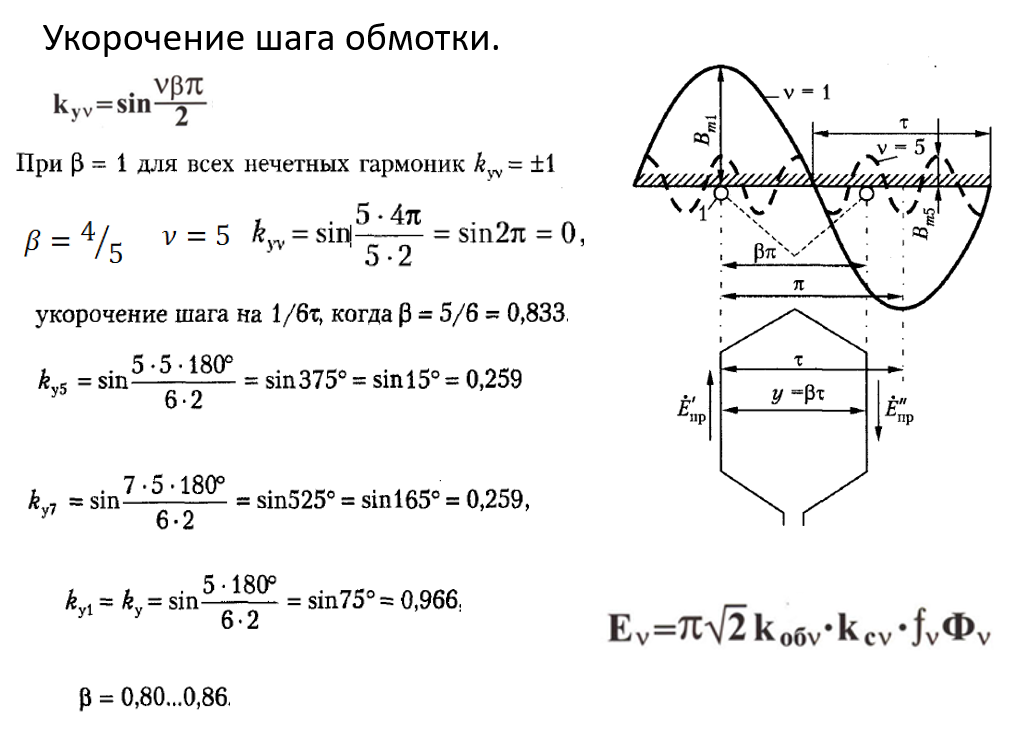
То есть при определённом β (примеры выше), у нас получается коэффициент укорочения = 0, то есть нет сдвига по фазе магнитной индукции между первым и вторым проводником. А значит и ЭДС какой-то гармоники = 0. А при каких-то красиво подобранных β, мы можем сделать коэффициент укорочения для нескольких гармоник не нулевым, но всё же близким к нулю (но при этом, главное, чтоб для основной гармоники коэффициент был близок к 1). Например так уменьшают 5ую и 7ую гармоники.

Влияние распределения обмотки.

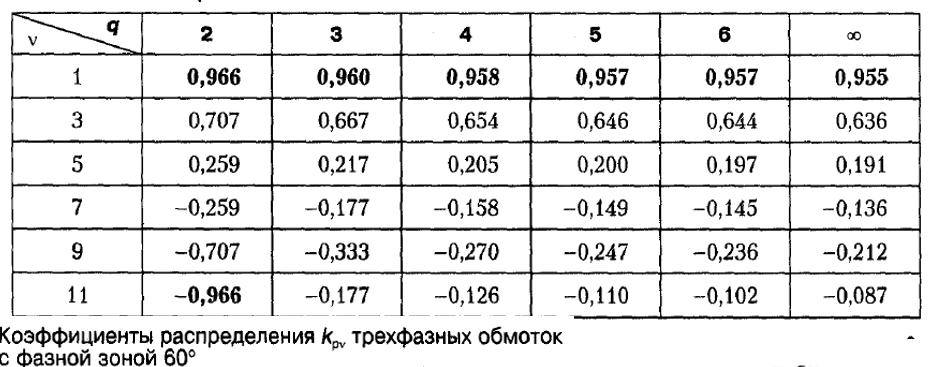
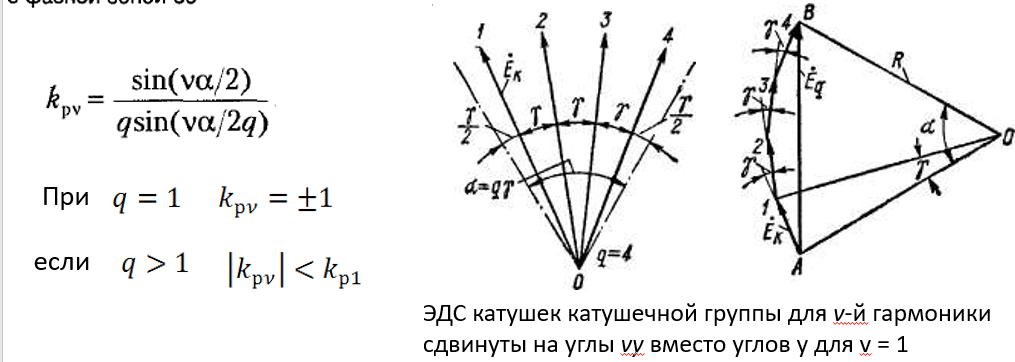
Для первой гармоники при любом q коэффициент распределения близок к единице, это опупенно. Для более высоких гармоник этот коэффициент становится меньше. Вот здесь формула коэффициента уже правильная.

Физическое пояснение. Пусть q=4. Между всеми ЭДС первой гармоники угол гамма. Они все геометрически суммируются. А если гармоника, например, 5ая, то угол уже будет 5*гамма. И тогда углы между ЭДС будут тупыми. И суммарная величина будет меньше.

Однако бывает такое (например q=2 и ν=11), что коэффициент распределения остался высоким. И вот такие подобные гармоники называются гармоники зубцового порядка.

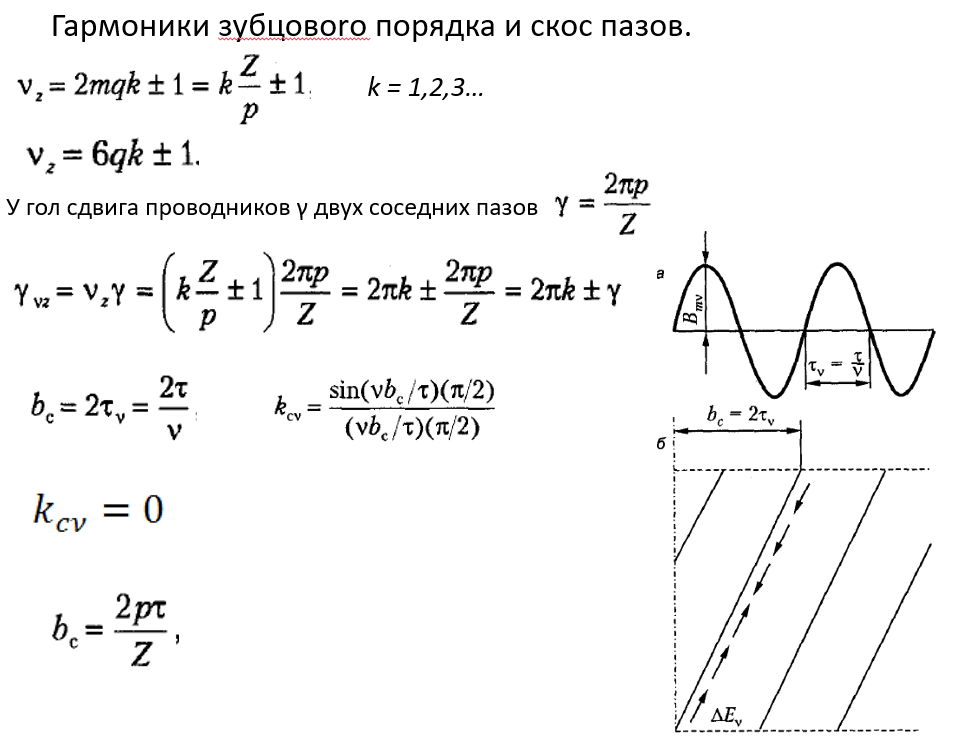
Номер гармоники зубцового порядка определяется по первой формуле. Напомню, что Z – число пазов. При m–числе фаз равным 3 получаем вторую формулу. При q=1 все гармоники являются гармониками зубцового порядка.

Рассмотрим угол сдвига проводников гамма у двух соседних пазов (формула на скрине). И тогда для гармоники зубцового порядка надо угол умножить на ν_z. Получаем опять угол гамма (так как 2πk это просто целое число оборотов).

Эти гармоники зубцового порядка являются высшими, и чем выше гармоника, тем меньше амплитуда, тем она слабее выражена. Поэтому, увеличивая q можно уменьшить эти гармоники.

Однако эти гармоники можно уменьшить и при помощи скоса пазов. Подгоняем скос пазов такой, чтобы коэффициент скоса был нулевым (или же близок к нулю). По рисунку (где график и развёртка статора) видно, что на положительную волну гармоники индукции ЭДС возникает в одну сторону, а на отрицательную в другую. И тогда общее ЭДС=0. Обычно скос равен зубцовому делению.

Кривая распределения индукции на полюсном делении реальной 3-х фазной обмотки также не косинусоидальная относительно оси поля. Она содержит ряд высших пространственных гармоник, несмотря на то, что при выполнении обмотки принимаются меры к их подавлению. В отличие от поля возбуждения СМ, эти гармоники не «склеены» между собой, а перемещаются относительно друг друга. Одна часть из них движется в сторону вращения первой гармоники, а другая в противоположном направлении. Поэтому результирующая кривая индукции несколько изменяется во времени.