2. Электродвижущие силы обмоток переменного тока

ЧИТАЙТЕ ВНИМАТЕЛЬНО, НА СЛАЙДАХ ОПЕЧАТКИ!!!

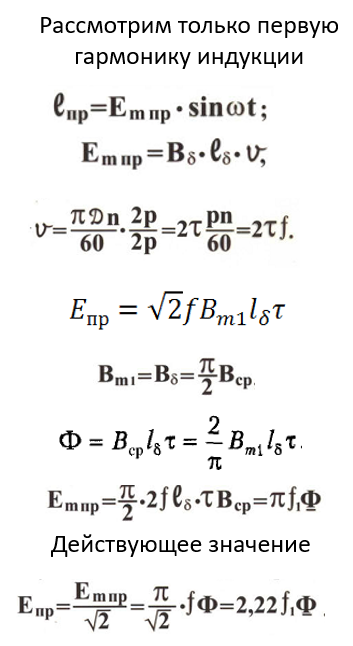
Распределение магнитной индукции вдоль поверхности статора.

Вообще, вот эта пунктирная линия – это то, как реально распределена магнитная индукция. Она имеет симметрию относительно горизонтальной оси. Значит, при разложении в ряд Фурье данная функция будет иметь только косинусные (потому что начало вертикальной оси находится в центре полюса) нечётные гармоники. Примерно можно сказать, что это прямоугольные импульсы, если полюса имели прямую форму, а не закруглённую.

Статоры АМ и СМ одинаковые, поэтому ЭДС в них возникают одинаково.

Стараются, чтобы ЭДС трёхфазной обмотки была по возможности синусоидальной. ЭДС создаётся вращающимся полем, и чтобы ЭДС было синусоидальным, важно, чтобы распределение магнитной индукции вдоль воздушного зазора было синусоидальным.

На рисунке показана синхронная явнополюсная машина. Штрихованная область – это статор. N и S – явные полюса синхронной машины. На полюсе обмотка возбуждения, создающая магнитный поток.

Магнитный поток делается синусоидальным за счёт геометрических размеров полюса. τ – полюсное деление: b_p – ширина полюсного наконечника. α – коэффициент полюсного перекрытия: . Этот коэффициент влияет на синусоидальность магнитной индукции. Обычно делают так, чтоб под серединой полюса зазор был минимальный, на краях зазор максимальный. И отношение .

Поле вращается с линейной скоростью v=2τf. (f – частота вращения поля)

Считаем, что поле чисто синусоидальное, и есть только первая гармоника. Тогда и ЭДС будет синусоидальна ( .

Амплитуда ЭДС проводника равна:

Где – амплитуда магнитной индукции первой гармоники

– расчётная активная длина машины.

Чтобы найти действующее значение, надо поделить амплитуду на , тогда

.

Если мы выразим амплитуду магнитной индукции через среднее значение, то мы можем прийти к формуле ЭДС через поток, приходящийся на один полюс:

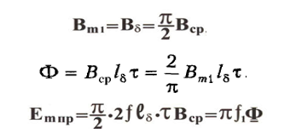
Теперь рассмотрим влияние скоса пазов.

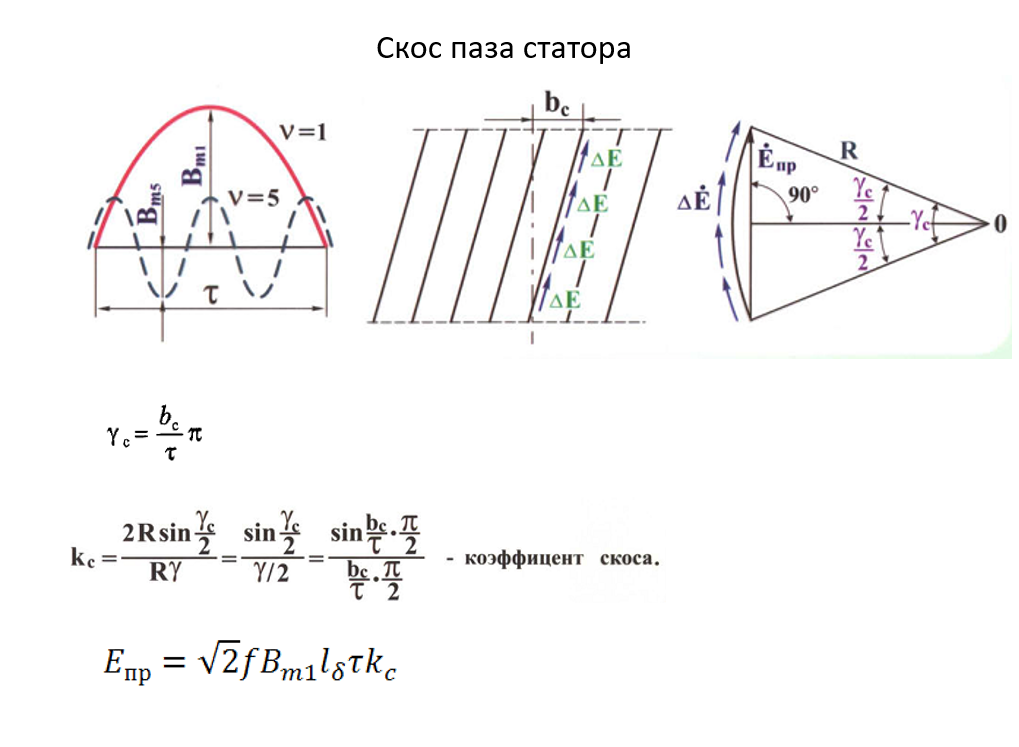
Часто пазы статора скашивают относительно магнитного поля. То есть они делаются под неким углом (в рисунке по середине это развёртка статора). Тогда проводники так же будут лежать в поле под некоторым углом. b_c – ширина скоса (величина скоса).

Так как проводник лежит под углом к полю, то каждая часть проводника (в которой образуется ЭДС ΔE) будет лежать под разным углом к полю. Эти ΔE будут сдвинуты по фазе. И уже мы должны их складывать геометрически (векторно), а не арифметически.

Арифметическая сумма этих ΔE будет дуга окружности (смотреть рисунок выше), а геометрическая сумма – хорда окружности – это будет E_пр с учётом скоса паза. И они опираются на центральный угол γ_с – угол скоса (на самом деле фиг знает, как величина называется, потому что в учебнике тоже не написано, а в лекции она сказала, что вот, всё опирается на угол гамма скоса).

Введём понятия k_c – коэффициент скоса (его формула показана на рисунке). Это отношение геометрической суммы ΔE (хорды) к алгебраической сумме ΔE (дуге). Величина показывает, на сколько ЭДС будет меньше из-за скоса. И ЭДС проводника надо будет домножить ещё на коэффициент скоса. Обычно коэффициент скоса 0,98.

ЭДС витка и катушки.

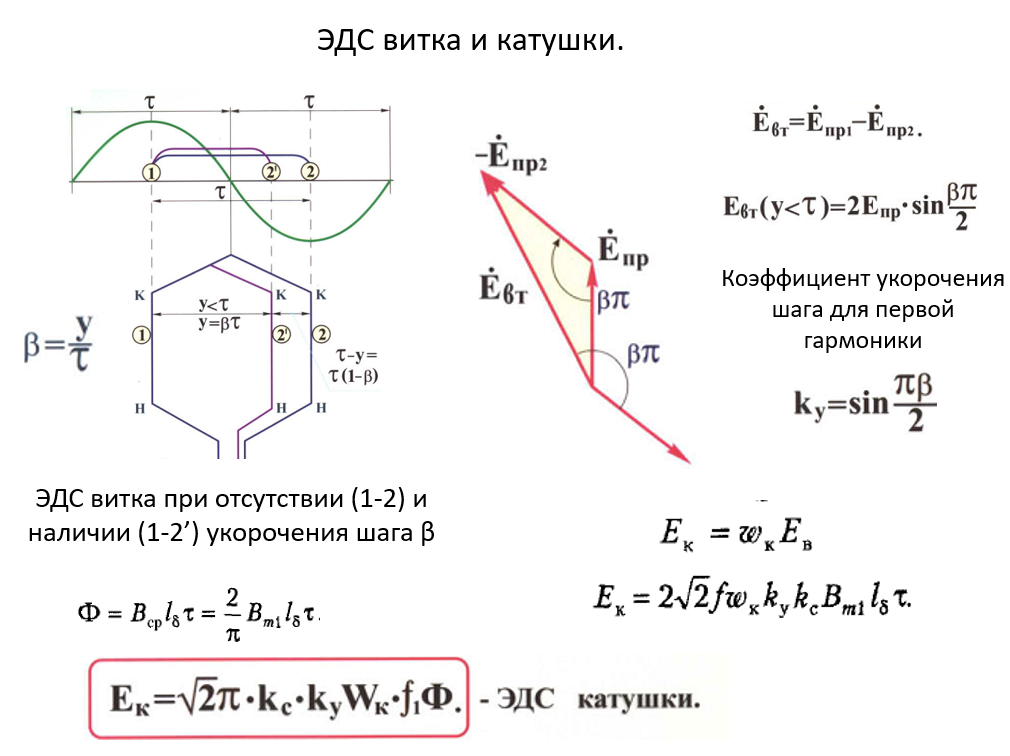
Зелёная линия на графике выше – распределение индукции в зазоре. Синяя линия – расположение витка.

Если бы наш виток имел шаг τ (первый проводник на позиции 1, второй проводник на позиции 2), то оба проводника находились бы под одной и той же индукции. И тогда ЭДС витка E_в это геометрическая разность ЭДС 1го и 2го провода, и это было бы E_в=2E_пр (т.к. сдвиг 180°, а величины ЭДС равны).

Обычно делается укорочение (β<1), но можно делать и удлинение (β>1), шага (2ой проводник на позиции 2') и наш шаг y меньше τ на величину β. β – относительный шаг и . Тогда второй проводник попадает под влияние другой магнитной индукции, которая сдвинута уже не на угол π (180°), а на угол βπ. И тогда надо будет геометрически вычитать вектора ЭДС проводника по равнобедренному треугольнику на рисунке выше. В итоге появляется k_у – коэффициент укорочения шага, показывает, как изменится ЭДС витка при укорочении шага. И опять E_пр надо домножить на коэффициент укорочения.

Катушка – группа последовательно соединённых витков, уложенных в одни и те же пазы и имеющие общую пазовую изоляцию от стенок паза. Поэтому у всех этих витков фаза одна и та же. И если мы ЭДС одного витка E_в умножим на число витков катушки w_к, то мы получим ЭДС катушки E_к­. И в итоге получаем формулу ЭДС катушки (красная рамка со скрина). ЭДС катушки зависит от частоты и от потока.

ЭДС катушечной группы. Обычно фаза состоит из нескольких катушечных групп (катушечная группа – совокупность последовательно соединённых катушек, лежащих в соседних пазах, и принадлежащих одной фазе). Z – число пазов; m – число фаз.

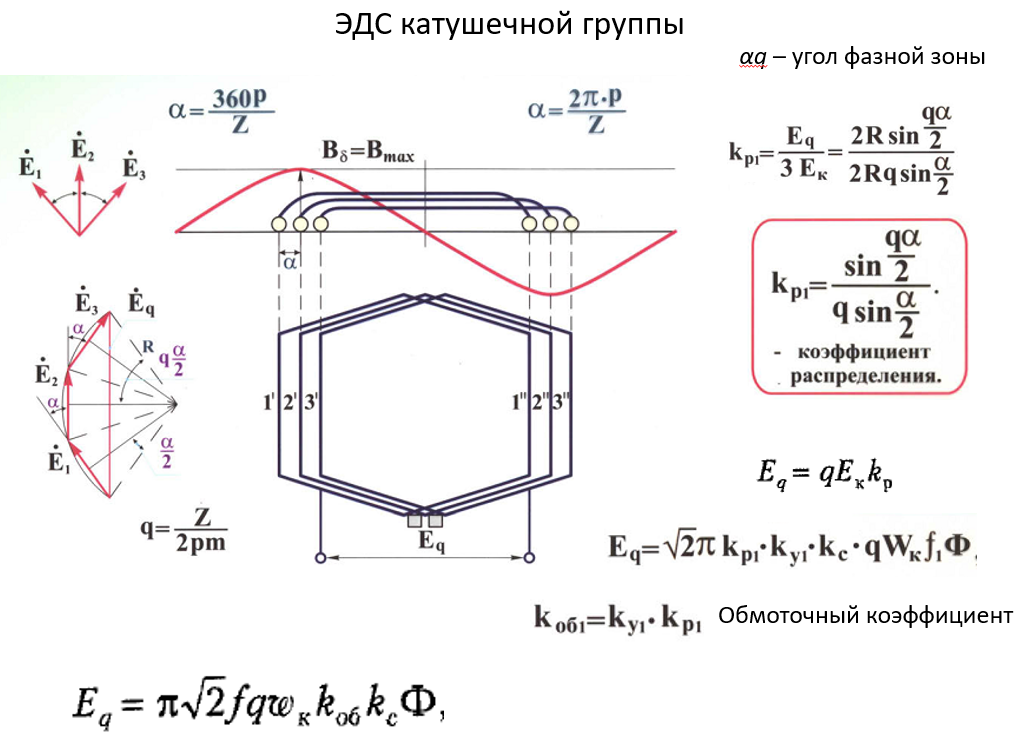
Угол сдвига соседних катушек равен α (формула выше). Число катушек q тоже на картине выше формула есть. Тогда αq – угол фазной зоны (типа, α показывает сдвиг между соседних катушек, как на рисунке между 1 и 2 точкой, а αq показывает сдвиг между 1 и 3 точкой).

Отдельные катушки находятся в магнитном поле с неким сдвигом по фазе этого поля. Если у нас N катушек (на слайде N=3), то надо учесть все сдвиги по фазе ЭДС. И опять геометрически просуммировать. И опять получится хорда, опирающаяся на угол αq, а одна ЭДС опирается на угол α.

Вводят понятие коэффициент распределения k_р – отношение ЭДС суммарной катушечной группы с учётом сдвига фаз, к арифметической сумме ЭДС всех катушек (формула на скрине в красной рамке, там q=3). Этот коэффициент распределения определяет, как уменьшится ЭДС из-за сдвига катушек. Если бы q=1, то был бы k_р=1.

Чтобы получить ЭДС катушечной группы E_q, надо умножить ЭДС катушки E_к на число катушек q и на коэффициент распределения k_р. И потом есть ещё обмоточный коэффициент (формула на картинке с опечаткой, вот правильная: ), это произведение коэф-та укорочения на коэф-т распределения.

ЭДС фазы обмотки. Каждая фаза состоит из нескольких катушечных групп. И обычно у нас все группы катушечные содержат одинаковое количество катушек q и поэтому занимают одинаковые углы α и сдвинуты относительно друг друга на целое число полюсных делений. Поэтому , где n – число катушечных групп.

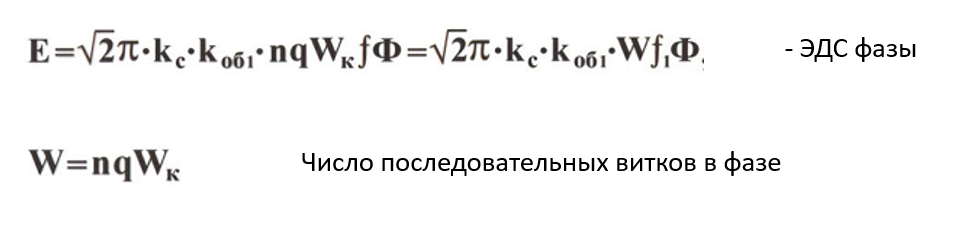
ПО ИТОГУ: ЭДС фазы зависит от геометрической формы всего нахуй на свете, частоты вращении поля, магнитного потока.