Системы массового обслуживания.
Текст программы:
%система
массового обслуживания
lambda=25;
mu=30;
n=5;
m=5;
ro=lambda/mu;
p0=0;
for
i=0:m
p0=p0+(ro^i)/(factorial(i));
end
p0=p0^(-1);
Potk=(ro^(n+m))*p0/((n^m)*factorial(n))
Q=1-Potk
A=lambda*Q
kzan=A/mu
roshki
= zeros(m,1);
for
i
= 1:m
roshki(i)
= i*ro^(i-1);
end
Loch=(ro^(n+1))*(sum(roshki))*p0/(n*factorial(n))
Toch=Loch/lambda
Lsist=Loch+kzan
Tsist=Lsist/lambda
Рассмотрим СМО в соответствии с нашим
вариантом и напишем текст программы
для расчета показателей ее эффективности.
Полученные результаты сведем в таблицу:
Показатель
|
Значение
|
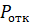
|
1.8722*10^-7
|
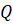
|
1
|
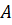
|
25
|
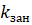
|
0.8333
|
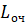
|
0.0023
|
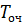
|
9.1968*10^-5
|
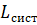
|
0.8356
|
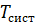
|
0.0334
|
Проанализировав полученные значения
показателей, можно сделать вывод, что
система эффективна, т.к. вероятность
отказа (вероятность того, что заявка
покинет СМО не обслуженной) стремится
к нулю и, как следствие относительная
пропуская способность (средняя доля
поступивших заявок, обслуживаемых
системой) равна 1. Также абсолютная
пропускная способность системы равна
интенсивности потока заявок, что
свидетельствует об эффективности
системы.
Остальные показатели также подтверждают
эффективность системы, хотя и средние
длина и время ожидания заявки в очереди
достаточно малы, но не близки к нулю.
Выводы: в ходе выполнения данной
лабораторной работы мы изучили методы
создания и анализа цепей Маркова, а
также научились рассчитывать показатели
эффективности систем массового
обслуживания. Для цепей Маркова были
получены матрицы переходов, графы и
промоделированы изменения состояний
системы при различном числе итераций.
Была получена оценка цепи Маркова. Для
систем массового обслуживания были
рассчитаны ключевые и другие характеристики
и дана оценка её эффективности.

