ТСП_2ЛР_В5
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра биотехнических систем
отчет
по лабораторной работе №2
по дисциплине «Теория случайных процессов»
Тема: БЕЛЫЙ ШУМ И СЛУЧАЙНЫЕ БЛУЖДАНИЯ
Вариант 5
Студентки гр. 9502 |
|
Камышанова О.А. Изланова А.Е. Позняк В.Ю. |
Преподаватель |
|
Скоробогатова А.И. |
Санкт-Петербург
2021
Цель работы: изучить концепции, лежащие в основе теории случайных процессов и получить навыки генерирования случайных блужданий и белого шума.
Базовые теоретические сведения
1. Белый шум
Простейшим случайным процессом ξ(n) является белый гауссовский шум, который представляет собой последовательность некоррелированных случайных переменных с нормальным распределением, где n – отсчеты времени, l – временной сдвиг (лаг).
Статистические характеристики
среднее по ансамблю
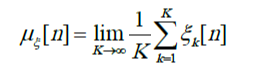
среднее по времени для k-й реализации
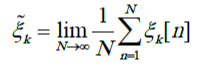
Важной
концепцией случайных процессов является
эргодичность, которая означает, что
статистические характеристики случайного
процесса, полученные в ходе усреднения
по времени, равны полученным при
усреднении по ансамблю. Для этого
необходимо, чтобы µξ[n]
= µξ независимо от n,
.
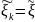Эргодичность связана со стационарностью
в широком смысле.
Важной характеристикой случайного процесса является выборочная корреляция по ансамблю:
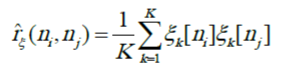
Мы называем ее «выборочной», поскольку K конечно, настоящее
среднее по
ансамблю
будет
получено при
.
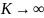Также важное значение играет нормированный коэффициент корреляции:
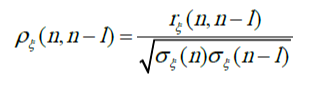
2. Случайные блуждания (винеровский процесс)
Для задания процесса со случайными блужданиями необходимо
рекурсивно генерировать последовательность:
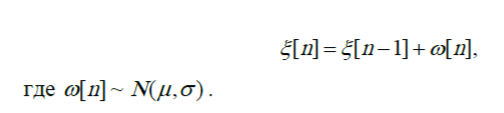
Положим, мы имеем дискретную случайную величину X, которая
принимает
конечное или счетное число значений
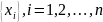с
вероятностями
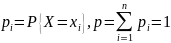(в общем случае, n может быть равно
).
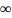3. Случайные блуждания с затуханием
Случайные блуждания с поглощением являются стационарным
случайным процессом и могут быть заданы следующим выражением:
где
.
Также, как и случайные блуждания, этот
процесс
является авто-регрессионным (AR) процессом первого порядка.
Так как данный процесс является стационарным для больших значений n, среднее по времени должно быть равно среднему по ансамблю. Тогда автокорреляция может быть рассчитана по одной реализации:
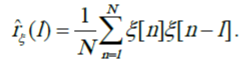
Ход работы
Белый шум
Код программы:
clear
close all
clc
%Белый шум
%1 - среднее по ансамблю, усреднение по реализации
N = 500; K = 1000; mu = 10; sigma = 1;
Ksi = normrnd(mu, sigma, [N, K]);
figure('Position', [50, 50, 800, 600], 'Name', '1.Белый шум',...
'NumberTitle', 'off');
Avg_r = zeros(N, K) + 1 / N * sum(Ksi, 1);
a = Avg_r(1 : N, 1);
subplot(1, 2, 1);
plot(1 : N, Avg_r);
Avg_a = 1 / K * sum(Ksi, 2);
hold on;
plot(1 : N, Avg_a, 'c');
set(gca, 'Ylim', [0, mu + sigma]);
title('Среднее по ансамблю и усреднения по реализациям');
%2 - диаграммы рассеяния
for i = 1 : 3
t = randi(N, 1, 2);
corr = 1 / K .* sum( Ksi(t(1), 1 : K)) / sigma;
subplot(3, 2, i * 2);
hold on;
scatter(Ksi( t(1), 1 : K), Ksi( t(2), 1 : K));
title(sprintf('r = %.3f', corr));
end
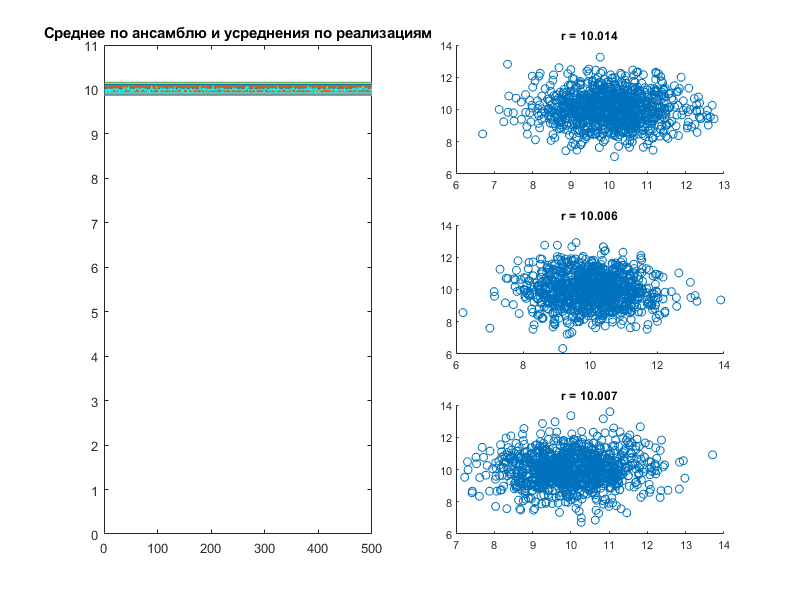
Рис. 1. Графики, полученные в результате программы Белый шум
Вывод: Процесс выглядит эргодическим, т. к. его усреднение по времени близко к усреднению по ансамблю и они сближаются с увеличением числа реализаций длин выборок
Примечание: 3 расположенных друг под другом графика на рис. 1. отражают совместное распределение для 3-х пар значений времени для ансамбля. Данные СВ коррелированы с коэффициентами r, также показанными на
рис. 1.
Случайные блуждания
Код программы:
clear
close all
clc
%Случайные блуждания
%6 - реализации случайных блужданий и скаттерограммы
N = 500; K = 1000; mu = 0; sigma = 1; l1 = 5; l2 = 50;
figure ('Name','Случайные блуждания')
dKsi = normrnd(mu, sigma, [N, K]); dKsi(1, 1 : K) = 0;
Ksi = cumsum(dKsi, 1);
plot(1 : N, Ksi);
title('Все реализации СП')
n1 = [10, 9; 50, 49; 100, 99; 200, 199];
n2 = [50, 40; 100, 90; 200, 190];
figure('Name', 'Диаграммы рассеяния');
subplot(2, 1, 1);
hold on
c = ['b', 'r', 'y', 'm']; sz = [40, 20, 10, 5];
for i = 4 : -1 : 1
scatter( Ksi(n1(i, 1), :), Ksi(n1(i, 2), :), sz(i), c(i));
end
xl = get(gca, 'Xlim');
grid on
title('Скаттерограмма (10,9),(50,49),(100,99),(200,199)');
subplot(2, 1, 2);
hold on
for i = 3 : -1 : 1
scatter( Ksi(n2(i, 1), :), Ksi(n2(i, 2), :), sz(i), c(i));
end
grid on
title('Скаттерограмма (50,40), (100,90), (200,190)');
%7 - автокоррелция по ансамблю
figure('Name', 'Автокоррелция по ансамблю')
ks = Ksi .* circshift(Ksi, 1, 1);
plot(ks);
ACF = mean(ks, 2);
plot(ACF);
ACF_theory = zeros(1, N);
hold on;
plot(1 : N, 0 : N - 1);
Полученные в результате графики:
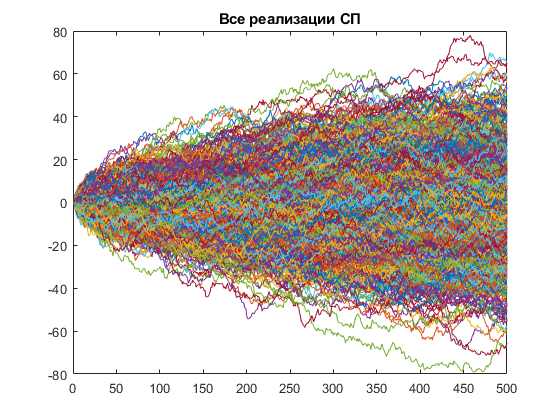
Рис. 2. Все реализации случайных блужданий
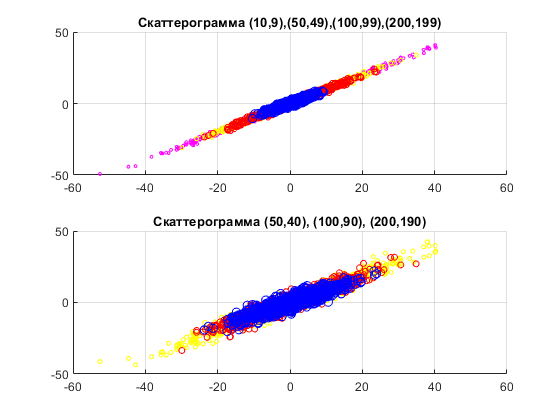
Рис. 3. Скаттерограмма случайных блужданий
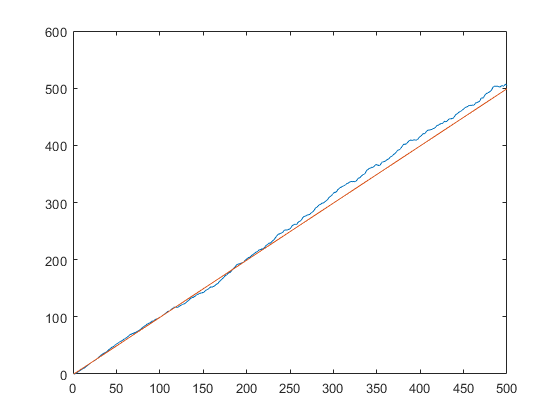
Рис. 4. Выборочная АКФ по ансамблю
Теоретические расчёты:
3) Для каждого
n математическое
ожидание будет
равно сумме
математических
ожиданий независимых друг от друга
шагов, а именно
,
где mu
– математическое
ожидание значения шага
4)
Т.к. шаги
независимы друг от
друга, то СКО
случайного процесса будет
складываться из СКО
каждого
шага,
а именно
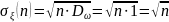, где
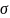– СКО
шага. При n→∞
СКО→∞.
5)
Аналогично
для
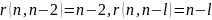
Вывод: Данный процесс нельзя назвать стационарный в широком смысле, r не зависит ни от n, ни от l.
При фиксированном l n→∞, подсчет r численным методом будет стремиться к 0.
6)
На рис. 2
совокупность реализаций СП выглядит,
как множество линий, лежащих вокруг
графиков функций
,
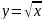что подтверждает полученную в пункте
(4) формулу.
Чем ближе скаттерограмма (рис. 3) к прямой y=x , тем лучше кореллируются абсциссы и ординаты точек. Скаттерограмма для шага 1 показывает большую кореллированность, чем для шага 10, следовательно для данной в задании длины случайного процесса (500 шагов) для расчёта М и СКО нужно брать усреднение по ансамблю. Значит, данный процесс нельзя назвать эргодическим.
7) Данный
процесс нельзя назвать эргодическим,
значит для каждой реализации будет свое
значение автокорелляции 
(n , n−l) и нельзя сделать оценку
автокорелляции по одной реализации,
нужен целый ансамбль (рис. 4).
Случайные блуждания с затуханием
Код программы:
clear
close all
clc
%Случайные блуждания c затуханием
N = 500; K = 1000; mu = 0; sigma = 1; l1 = 5; l2 = 50;
%9 - генерация случайных блужданий
figure('Name', '9.1');
dKsi = normrnd(mu, sigma, [N, K]);
dKsi(1, :) = 0;
Ksi = zeros(1, K);
for i = 2 : N
Ksi(i, :) = Ksi(i - 1, :) * 0.9 + dKsi(i, :);
end
plot(1 : N, Ksi);
title('Все реализации СП')
figure('Name', '9.2');
n1 = [10, 9; 50, 49; 100, 99; 200, 199];
n2 = [50, 40; 100, 90; 200, 190];
subplot(2, 1, 1);
hold on
c = ['b', 'r', 'y', 'm'];
sz = [40, 20, 10, 5];
for i = 4 : -1 : 1
scatter( Ksi(n1(i, 1), :), Ksi(n1(i, 2), :), sz(i), c(i));
end
xl = get(gca, 'Xlim');
grid on
title('Скаттерограмма (10,9),(50,49),(100,99),(200,199)');
subplot(2, 1, 2);
hold on
for i = 3 : -1 : 1
scatter( Ksi(n2(i, 1), :), Ksi(n2(i, 2), :), sz(i), c(i));
end
grid on
title('Скаттерограмма (50,40), (100,90), (200,190)');
%10 - выборочна АКФ
mean_ksi = mean(Ksi .* circshift(Ksi, 1, 1), 2) ;
figure('Name', 'Выборочная АКФ по ансамблю');
hold on
plot(mean_ksi);
x = 0 : N-1;
y = 0.05*(1 - 0.9 .^ x) ./ (1 - 0.9) .^ 2;
plot(y);
Полученные в результате графики:
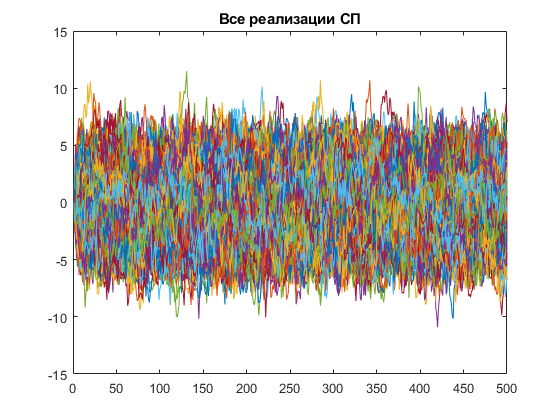
Рис. 5. Все реализации случайных блужданий с затуханием
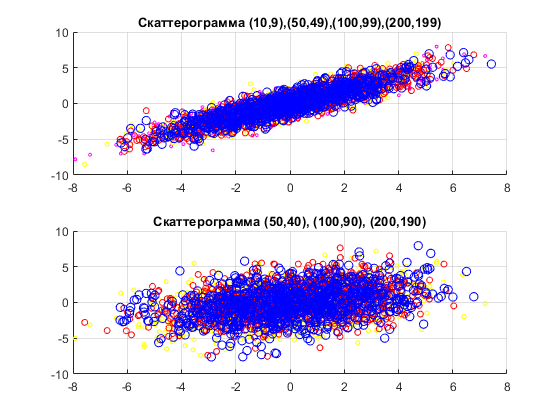
Рис. 6. Скаттерограмма случайных блужданий с затуханием
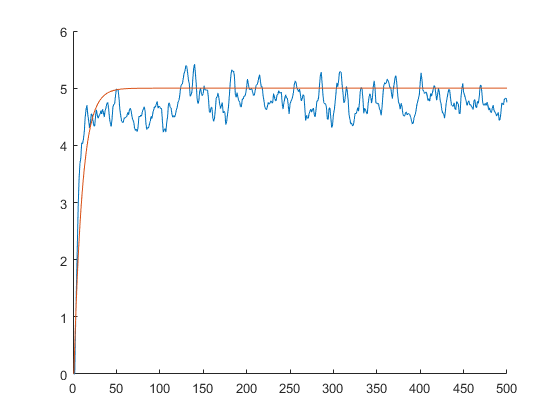
Рис. 7. Выборочная АКФ по ансамблю
Теоретические расчёты:
8)
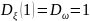
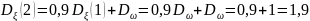
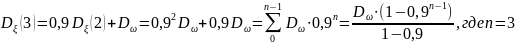и т.д.
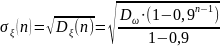
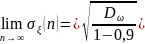
Процесс не является стационарным в широком смысле, т.к. его дисперсия, СКО и математическое ожидание не зависят от n.
9) На рис. 5. видно, что процесс не является эргодическим (реализации отличаются друг от друга), но СКО графиков (рис. 6) стремится или остается около своего предельного значения, что было доказано теоретическими расчетами.
В сравнении с п.6 скаттерограмма получилась более рассеянная, но для первого шага отклонения меньше, чем для десятого.
10) Среднее по ансамблю r и по времени (рис. 7.) больше всего сходе для l2. С ростом K и N будут приближаться друг к другу среднее по времени и по ансамблю для l2.
Вывод:
В ходе лабораторной работы были изучены концепции, лежащие в основе теории случайных процессов и получены навыки генерирования случайных блужданий и белого шума, теоретические расчеты и графические зависимости и сравнения представлены в ходе работы.