
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра программного обеспечения информационных технологий
Факультет ФКСиС
Специальность ПОИТ
Контрольная работа №1
по дисциплине «Методы оптимизации»
Тема «Линейная оптимизация. Модели распределения ресурсов. Элементы теории двойственности. Теория игр»
Вариант 4
Выполнил студент: Бордон Е.С.
группа 991051
Зачетная книжка № 99105004
Минск 2021
Задание 1:
1. Составить математическую модель задачи. Объяснить экономический смысл переменных.
2. Составить математическую модель двойственной задачи. Объяснить экономический смысл двойственных переменных.
3. Найти оптимальный план выпуска продукции, обеспечивающий максимальную прибыль.
4. Провести анализ оптимальных решений прямой и двойственной задач, используя отчеты трех типов (по результатам, по устойчивости, по пределам):
а) указать, какая продукция вошла в оптимальный план, и насколько невыгодно производство продукции, не вошедшей в оптимальный план,
б) указать дефицитные и избыточные ресурсы,
в) выписать оптимальное решение двойственной задачи,
г) указать наиболее дефицитный ресурс, исходя из оптимального решения двойственной задачи,
д) указать интервал устойчивости двойственных оценок,
5. Решить двойственную задачу. Сравнить решение с полученным
в пункте 4.
6. Выяснить, как изменится выпуск продукции и значение целевой функции, при изменении каждого из имеющихся ресурсов на единицу. Оценить раздельные и суммарное изменения.
Вариант 4:
На приобретение оборудования для нового производственного участка выделено 30 тыс. ден. ед. И помещение площадью в 45 м кв. Участок может быть оснащен машинами трех типов, характеристики которых приведены в таблице:
Марка машины |
Стоимость машины, тыс. ден. ед. |
Занимаемая площадь, м кв. |
Производительность за смену, тыс. ед. |
М1 |
6 |
9 |
8 |
М2 |
3 |
4 |
4 |
М3 |
2 |
3 |
3 |
Найти оптимальный план приобретения машин, обеспечивающий новому производственному участку максимальную производительность.
Решение:
Обозначим неизвестное количество оборудования М1, М2 и М3 видов соответственно через x1, x2 и x3.
Функция цели может быть записана следующим образом:
F(x) = 8x1 + 4x2+3x3 (max);
Ограничения по площади:
9x1 + 4x2 + 3x3 ≤ 45;
Ограничения по стоимости:
6x1 + 3x2 + 2x3 ≤ 30;
Ограничения на знак переменных:
x1 ≥ 0; x2 ≥ 0; x3 ≥ 0;
Преобразуем неравенства в равенства добавлением неотрицательных переменных:
8x1 + 4x2 + 3x3 + 0x4 + 0x5 → max
9x1 + 4x2 + 3x3 + 1x4 + 0x5 = 45
6x1 + 3x2 + 2x3 + 0x4 + 1x5 = 30
x1, x2, x3, x4, x5 ≥ 0
Матрица коэффициентов A=ǁaijǁ системы уравнений имеет вид:
9 |
4 |
3 |
1 |
0 |
6 |
3 |
2 |
0 |
1 |
Правая часть ограничений системы уравнений B имеет вид:
45 |
30 |
Целевая функция C имеет вид:
8 |
4 |
3 |
0 |
0 |
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1.
Базисные векторы x4, x5, следовательно, все элементы в столбцах x4, x5, ниже горизонтальной линии должны быть нулевыми.
Симплекс таблица примет вид:
Таблица 1:
Базис |
х0 |
xl |
х2 |
х3 |
х4 |
х5 |
х4 |
45 |
9 |
4 |
3 |
1 |
0 |
х5 |
30 |
6 |
3 |
2 |
0 |
1 |
|
0 |
-8 |
-4 |
-3 |
0 |
0 |
Запишем текущий опорный план:
Х = (0 0 0 45 30)
Значение целевой функции в данной точке:
F = C⋅X = 8⋅0 + 4⋅0 + 3⋅0 + 0⋅45 + 0⋅30 = 0
Данный опорный план не является оптимальным, так как на пересечении строки 3 и столбцов x1, x2, x3, x4, x5 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-8), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,1), при ai,1>0, i=1,...2. min(45:9, 30:6)=5 соответствует строке 1. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки 2, 3 со строкой 1, умноженной на -2/3, 8/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Таблица 2:
Базис |
х0 |
xl |
х2 |
х3 |
х4 |
х5 |
х4 |
5 |
1 |
4/9 |
1/3 |
1/9 |
0 |
х5 |
0 |
0 |
1/3 |
0 |
-2/3 |
1 |
|
40 |
0 |
-4/9 |
-1/3 |
8/9 |
0 |
Запишем текущий опорный план:
Х = (5 0 0 0 0)
Значение целевой функции в данной точке:
F = C⋅X = 8⋅5 + 4⋅0 + 3⋅0 + 0⋅0 + 0⋅0 = 40
Данный опорный план не является оптимальным, так как на пересечении строки 3 и столбцов x1, x2, x3, x4, x5 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-4/9), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,2), при ai,2>0, i=1,...2. min(5:4/9, 0:1/3)=0 соответствует строке 2. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки 1, 3 со строкой 2, умноженной на -4/3, 4/3, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Таблица 3:
Базис |
х0 |
xl |
х2 |
х3 |
х4 |
х5 |
х4 |
5 |
1 |
0 |
1/3 |
1 |
-4/3 |
х5 |
0 |
0 |
1 |
0 |
-2 |
3 |
|
40 |
0 |
0 |
-1/3 |
0 |
4/3 |
Запишем текущий опорный план:
Х = (5 0 0 0 0)
Значение целевой функции в данной точке:
F = C⋅X = 8⋅5 + 4⋅0 + 3⋅0 + 0⋅0 + 0⋅0 = 40
Данный опорный план не является оптимальным, так как на пересечении строки 3 и столбцов x1, x2, x3, x4, x5 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-1/3), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,3), при ai,3>0, i=1,...2. min(5:1/3)=15 соответствует строке 1. Из базиса выходит вектор x1. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 1Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Таблица 4:
Базис |
х0 |
xl |
х2 |
х3 |
х4 |
х5 |
х4 |
15 |
3 |
0 |
1 |
3 |
-4 |
х5 |
0 |
0 |
1 |
0 |
-2 |
3 |
|
45 |
1 |
0 |
0 |
1 |
0 |
Запишем текущий опорный план:
Х = (0 0 15 0 0)
Значение целевой функции в данной точке:
F = C⋅X = 8⋅0 + 4⋅0 + 3⋅15 + 0⋅0 + 0⋅0 = 45
Текущий опорный план является оптимальным, так как в последней строке нет отрицательных элементов.
Решение канонической задачи можно записать так:
Х0* = (0 0 15 0 0)
Решение исходной задачи:
Х* = (0 0 15)
x1=0, x2=0, x3=15
Значение целевой функции в оптимальной точке:
F = Cисх⋅X∗ = 8⋅0 + 4⋅0 + 3⋅15 = 45
где Cисх − коэффициенты целевой функции исходной задачи.
Ответ: машин М3 – 15шт, производительность равна 45тыс. ед.
Проверка средствами EXCEL:
Исходные данные:
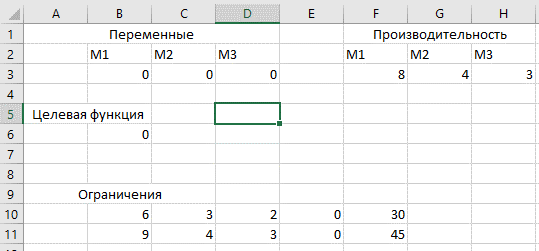
Рис1. Microsoft Excel
Заполним формулы для целевой функции и ограничений:
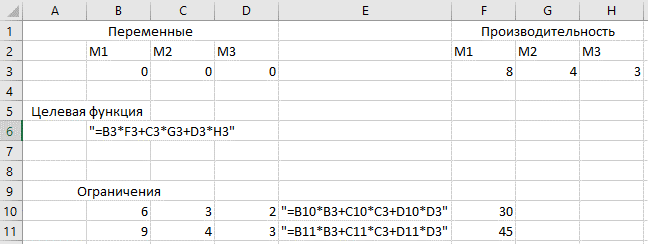
Рис2. Microsoft Excel
Выполним настройку поиска решения:
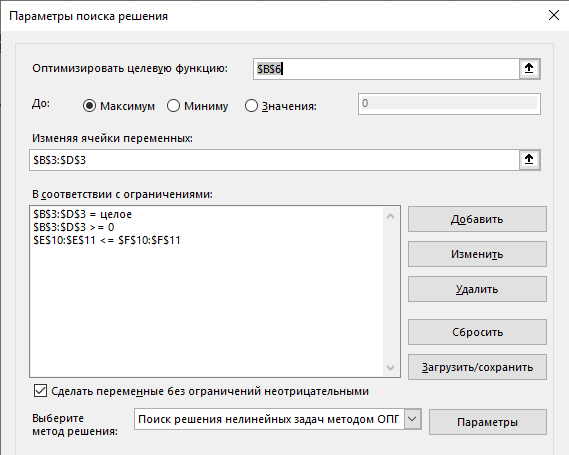
Рис3. Microsoft Excel
Полученный результат:
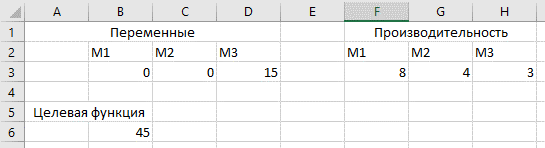
Рис4. Microsoft Excel
Ответ: машин М3 – 15шт, производительность равна 45тыс. ед.
Попробуем изменить каждый имеющийся ресурс на одну единицу:
Увеличиваем Стоимость на 1 единицу и занимаемую площадь на 1 единицу.
Таблица 5:
Марка машины |
Стоимость машины, тыс. ден. ед. |
Занимаемая площадь, м кв. |
Производительность за смену, тыс. ед. |
М1 |
7 |
10 |
8 |
М2 |
4 |
5 |
4 |
М3 |
3 |
4 |
3 |
Решать будем с помощью таблицы Excel.
Исходные данные с учетом изменившихся условий:
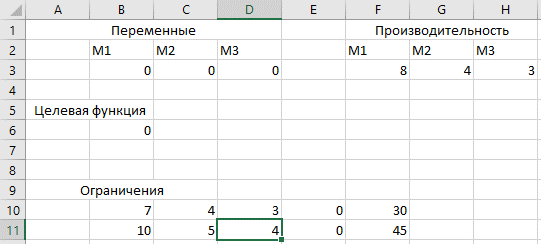
Рис5. Microsoft Excel
Данные после обработки:
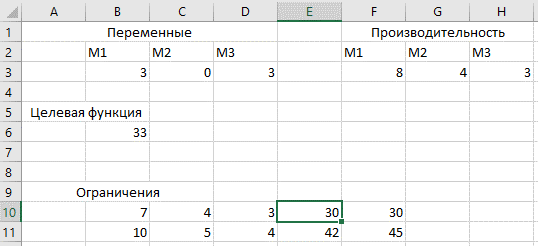
При увеличении на одну единицу стоимости машин и занимаемой ими площади, а также сохранении производительности и остальных параметров ответ меняется. Становится выгоднее приобрести 3 машины М1 и 3 машины М3 с суммарной производительностью в 33 тыс.ед.
Выводы:
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.
Задание 2:
1) Составить математическую модель транспортной задачи;
2) Решить транспортную задачу без учета дополнительных ограничений на перевозки;
3) Решить транспортную задачу с дополнительными ограничениями на перевозки.
4) Сделать выводы.
Вариант 4:
Вариант |
Задача |
||||
4 |
X42≤50, X24 ≥50 |
||||
al \ bj |
50 |
100 |
100 |
100 |
|
50 |
2 |
4 |
5 |
8 |
|
100 |
5 |
3 |
4 |
6 |
|
50 |
3 |
1 |
2 |
4 |
|
100 |
7 |
2 |
6 |
9 |
|
Решение:
Число пунктов отправления m=4, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=4+4−1=7 заполненных клетках таблицы. Тарифы перевозок единицы груза из каждого пункта отправления во все пункты назначения задаются матрицей
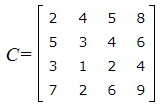
Наличие груза у поставщиков равно:
![]()
Общая потребность в грузе в пунктах назначения равна:
![]()
∑ Ai<∑ Bi. Модель транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительный пункт отправления A5 c запасами 350− 300=50. Тарифы перевозки из пункта отправления A5 во все пункты назначения полагаем равными нулю. В результате получим закрытую модель транспортной задачи:
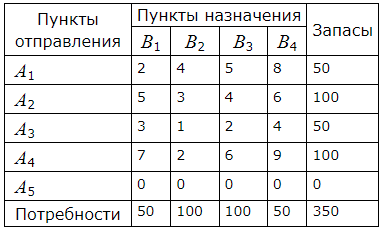
Найдем опорный план задачи методом северно-западного угла.
A1≤B1. Следовательно в клетку (A1, B1) помещаем число min(A1, B1 )=50. Запасы пункта A1 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A1 и будем считать потребности пункта B1 равными 50−50=0.
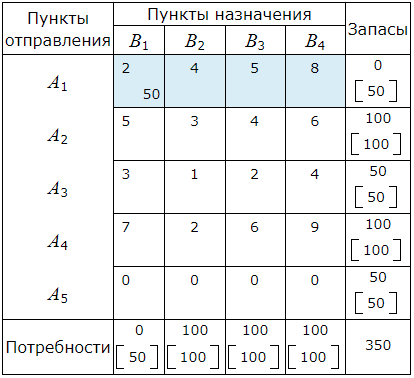
A2>B1. Следовательно в клетку (A2, B1) помещаем число min(A2, B1)=0. Потребности пункта B1 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B1 и будем считать запасы пункта A2 равными 100−0=100.
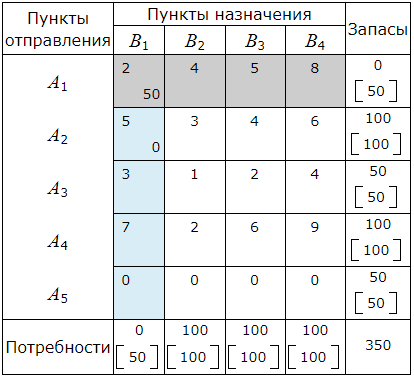
A2≤B2. Следовательно в клетку (A2, B2 ) помещаем число min(A2, B2 )=100. Запасы пункта A2 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A2 и будем считать потребности пункта B2 равными 100−100=0.
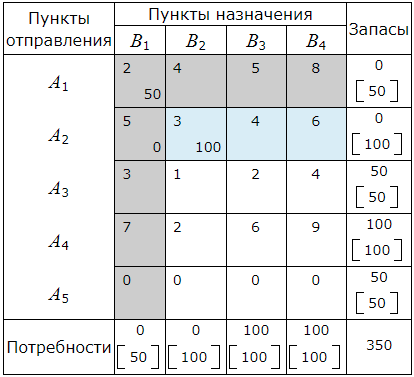
A3>B2. Следовательно в клетку (A3, B2) помещаем число min(A3, B2)=0. Потребности пункта B2 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B2 и будем считать запасы пункта A3 равными 50−0=50.
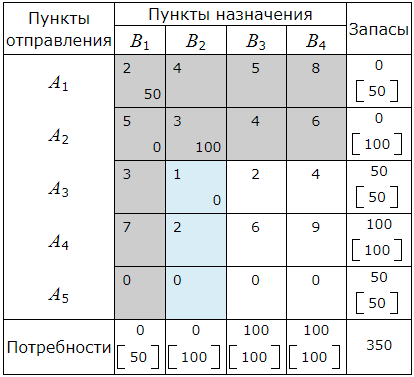
A3≤B3. Следовательно в клетку (A3, B3 ) помещаем число min(A3, B3 )=50. Запасы пункта A3 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A3 и будем считать потребности пункта B3 равными 100−50=50.
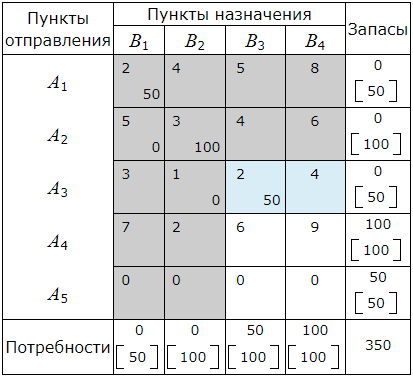
A4>B3. Следовательно в клетку (A4, B3) помещаем число min(A4, B3)=50. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A4 равными 100−50=50.
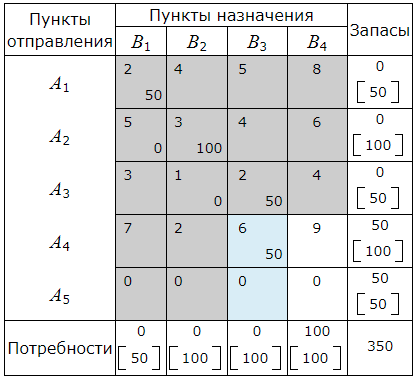
A4≤B4. Следовательно в клетку (A4, B4 ) помещаем число min(A4, B4 )=50. Запасы пункта A4 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A4 и будем считать потребности пункта B4 равными 100−50=50.
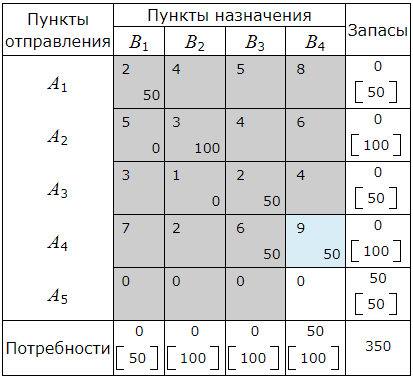
A5≤B4. Следовательно в клетку (A5, B4 ) помещаем число min(A5, B4 )=50. Запасы пункта A5 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A5 и будем считать потребности пункта B4 равными 50−50=0.
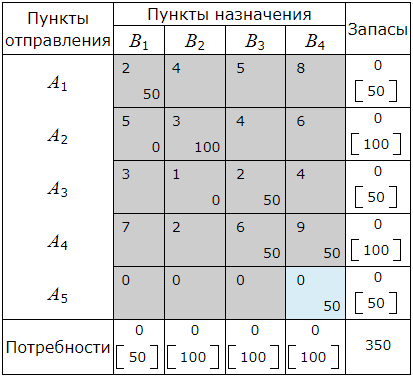
Найдем оптимальный план транспортной задачи методом потенциалов.
Опорный план имеет следующий вид:
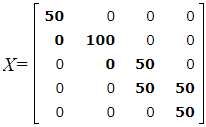
При этом плане стоимость перевозок вычисляется так:
S=2·50 +5·0+ 3·100 +1·0+ 2·50+ 6·50+ 9·50+ 0·50= 1250
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 8 уравнений с 9 неизвестными:
β1−α1=2; β1−α2=5; β2−α2=3; β2−α3=1; β3−α3=2; β3−α4=6; β4−α4=9; β4−α5=0;
Полагая α1=0, находим β1=2 α2=-3 β2=0 α3=-1 β3=1 α4=-5 β4=4 α5=4 .
α12=-4, α13=-4, α14=-4, α23=0, α24=1, α31=0, α34=1, α41=0, α42=3, α51=-2, α52=-4, α53=-3.
Полученные числа заключаем в рамки и записываем их в соответствующие клетки таблицы:
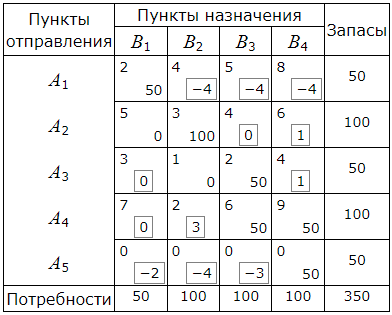
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 3 находится в пересечении строки A4 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочередно знаки "−" и "+".
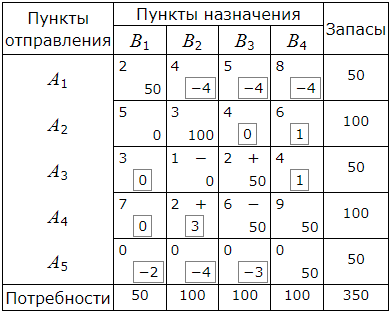
Наименьшее из чисел в минусовых клетках равно 0. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках, добавляется 0, а из чисел, находящихся в минусовых клетках, вычитается это число.
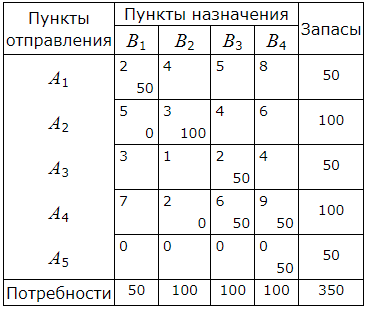
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
S=2·50 +5·0+ 3·100 +2·50 +2·0+ 6·50+ 9·50+ 0·50= 1250
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 8 уравнений с 9 неизвестными:
β1−α1=2; β1−α2=5; β2−α2=3; β3−α3=2; β2−α4=2; β3−α4=6; β4−α4=9; β4−α5=0;
Полагая α1=0, находим β1=2 α2=-3 β2=0 α4=-2 β3=4 β4=7 α3=2 α5=7.
Для каждой свободной клетки вычисляем число αij=βj−αi−cij:
α12=-4, α13=-1, α14=-1, α23=3, α24=4, α31=-3, α32=-3, α34=1, α41=-3, α51=-5, α52=-7, α53=-3.
Полученные числа заключаем в рамки и записываем их в соответствующие клетки таблицы:
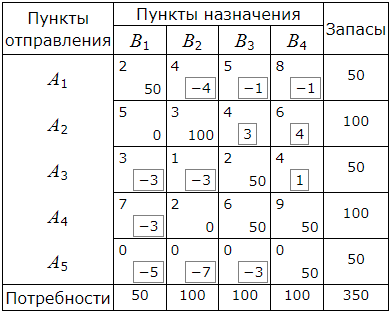
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 4 находится в пересечении строки A2 и столбца B4. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочередно знаки "−" и "+".
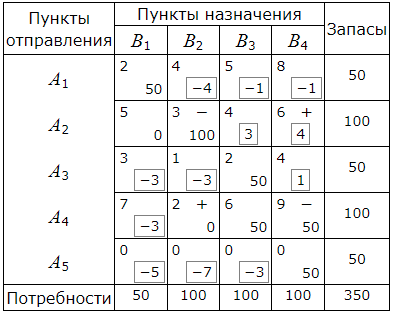
Наименьшее из чисел в минусовых клетках равно 50. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках, добавляется 50, а из чисел, находящихся в минусовых клетках, вычитается это число.
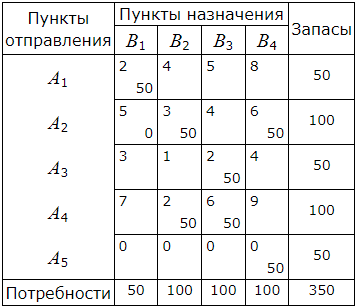
Опорный план имеет следующий вид:
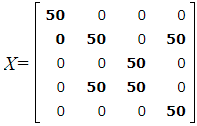
При этом плане стоимость перевозок вычисляется так:
S=2·50 +5·0+ 3·50+ 6·50+ 2·50+ 2·50+ 6·50+ 0·50= 1050
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 8 уравнений с 9 неизвестными:
β1−α1=2; β1−α2=5; β2−α2=3; β4−α2=6; β3−α3=2; β2−α4=2; β3−α4=6; β4−α5=0;
Полагая α1=0, находим β1=2 α2=-3 β2=0 β4=3 α4=-2 α5=3 β3=4 α3=2 .
Для каждой свободной клетки вычисляем число αij=βj−αi−cij:
α12=-4, α13=-1, α14=-5, α23=3, α31=-3, α32=-3, α34=-3, α41=-3, α44=-4, α51=-1, α52=-3, α53=1.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
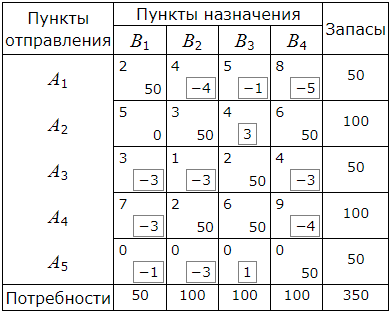
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 3 находится в пересечении строки A2 и столбца B3. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак "+" а остальные клетки цикла поочередно знаки "−" и "+".
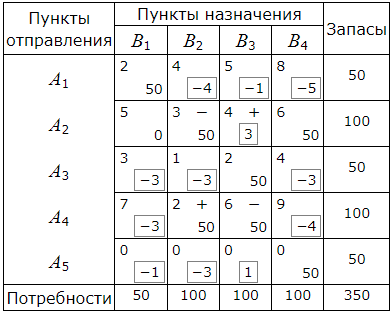
Наименьшее из чисел в минусовых клетках равно 50. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках, добавляется 50, а из чисел, находящихся в минусовых клетках, вычитается это число.
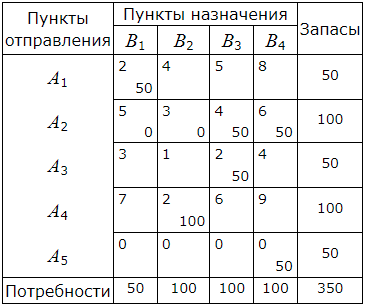
Опорный план имеет следующий вид:
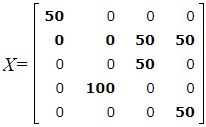
При этом плане стоимость перевозок вычисляется так:
S=2·50 +5·0+ 3·0+4 ·50+6·50+2·50+2· 100+0·50=900
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 8 уравнений с 9 неизвестными:
β1−α1=2; β1−α2=5; β2−α2=3; β3−α2=4; β4−α2=6; β3−α3=2; β2−α4=2; β4−α5=0;
Полагая α1=0, находим β1=2 α2=-3 β2=0 β3=1 β4=3 α4=-2 α3=-1 α5=3 .
Для каждой свободной клетки вычисляем число αij=βj−αi−cij:
α12=-4, α13=-4, α14=-5, α31=0, α32=0, α34=0, α41=-3, α43=-3, α44=-4, α51=-1, α52=-3, α53=-2.
Полученные числа заключаем в рамки и записываем их в соответствующие клетки таблицы:
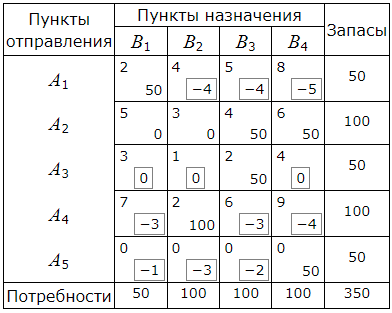
Среди чисел αij нет положительных. Следовательно данный опорный план является оптимальным.
Ответ:
Оптимальный план имеет следующий вид:
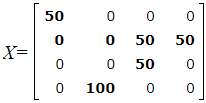
При этом плане стоимость перевозок вычисляется так:
S=2·50 +5·0+ 3·0+4 ·50+6·50+2·50+2· 100=900
При этом плане остается неудовлетворенным потребности (50) пункта B4.
Распределение ресурсов:
Из склада A1 отправить груз (50) в пункт B1
Из склада A2 отправить груз (50) в пункт B3
Из склада A2 отправить груз (50) в пункт B4
Из склада A3 отправить груз (50) в пункт B3
Из склада A4 отправить груз (100) в пункт B2
Сделаем проверку средствами Excel
Создадим таблицу с исходными данными сразу открытого типа:
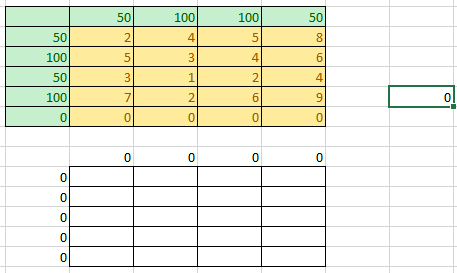
Рис. 6 Excel
Зададим условия поиска решения:
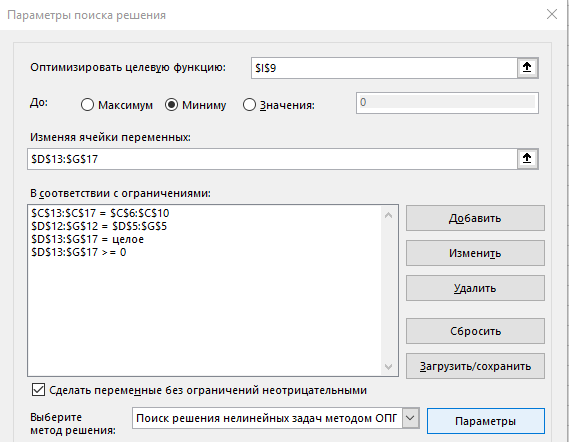
Рис. 7 Excel
Результаты поиска решения:
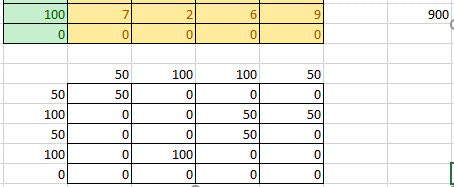
Рис. 8 Excel
В результате работы программы были получены аналогичные результаты.
Выполним условия по ограничения X42≤50, X24 ≥50. Расчеты будем производить в таблице Excel. Для этого в параметрах поиска решения добавим новые условия:

Рис. 9 Excel
В результате работы программы ошибок не было обнаружено и было найдено оптимальное решение:

Рис.10 Excel
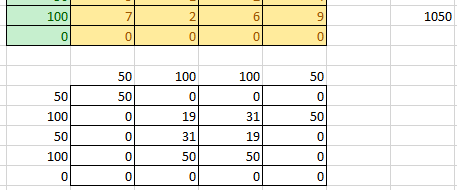
Рис.11 Excel
Оптимальный план имеет следующий вид:

При этом плане стоимость перевозок вычисляется так:
S=2·50 +3·19+1·31+2·50+4·31+2·19+6·50+6·50=1050
При этом плане остается неудовлетворенным потребности (50) пункта B4.
Распределение ресурсов:
Из склада A1 отправить груз (50) в пункт B1
Из склада A2 отправить груз (19) в пункт B2
Из склада A2 отправить груз (31) в пункт B3
Из склада A2 отправить груз (50) в пункт B4
Из склада A3 отправить груз (31) в пункт B2
Из склада A3 отправить груз (19) в пункт B3
Из склада A4 отправить груз (50) в пункт B2
Из склада A4 отправить груз (50) в пункт B3
Выводы:
Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи гораздо быстрее и удобнее использовать программные алгоритмы решения.
Задание 3:
После нескольких лет эксплуатации промышленное оборудование оказывается в одном из следующих состояний:
1) оборудование может использоваться в очередном году после профилактического ремонта;
2) для безаварийной работы оборудования в дальнейшем следует заменить отдельные его детали и узлы;
3) оборудование требует капитального ремонта или замены.
В зависимости от сложившейся ситуации руководство предприятия в состоянии принять такие решения: 1) отремонтировать оборудование силами заводских специалистов, что потребует, в зависимости от обстановки, затрат, равных а1, а2 или а 3 ден. ед.; 2) вызвать специальную бригаду ремонтников, расходы в этом случае составят b1, b2 или b3 ден. ед.; 3) заменить оборудование новым, реализовав устаревшее оборудование по его остаточной
стоимости; совокупные затраты в результате этого мероприятия будут равны соответственно с1, с2 или с3 ден. ед. Указанные выше расходы предприятия включают кроме стоимости ремонта и заменяемых деталей, и узлов убытки, вызванные ухудшением качества выпускаемой продукции, простоем неисправного оборудования, а также затраты на установку и отладку нового оборудования. Требуется:
1) придать описанной ситуации игровую схему, установить характер игры и выявить ее участников, указать возможные чистые стратегии сторон;
2) составить платежную матрицу;
3) выяснить, какое решение о работе оборудования в предстоящем году целесообразно рекомендовать руководству предприятия, чтобы минимизировать потери при следующих предположениях:
а) накопленный на предприятии опыт эксплуатации аналогичного оборудования показывает, что вероятности указанных выше состояний оборудования равны соответственно q1, q2, q3;
б) имеющийся опыт свидетельствует о том, что все три возможных состояния оборудования равновероятны;
в) о вероятностях состояний оборудования ничего определенного сказать нельзя.
Указание. В п. 3 следует найти оптимальные чистые стратегии, пользуясь: в п. 3) а) — критерием Байеса, в п. 3) б) — критерием Лапласа, в п. 3) в) — критериями Вальда, Сэвиджа, Гурвица (значение параметра У в критерии Гурвица задается).
4) Решить в смешанных стратегиях (сведением к задаче линейного программирования).
Вариант 4 |
||||||||||||
а1 |
а2 |
а3 |
b1 |
b2 |
b3 |
c1 |
c2 |
c3 |
q1 |
q2 |
q3 |
Ꝩ |
6 |
10 |
15 |
15 |
9 |
18 |
13 |
24 |
12 |
0,15 |
0,55 |
0,30 |
0,80 |
