Econometrics

Добавил:

yuliia10293 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный экономический университет им. В. Гетьмана

Предмет:

Моделирование

Файл:

(i 1, n) .

(i 1, n) .

.pdf

Скачиваний:

Добавлен:

28.01.2022

Размер:

4.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 558 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Неважко побачити, що x1=1; x2=–2; x3=–1; розв’язками системи (3.38) будуть і ці самі значення, помножені на будь-які числа, які задовольняють рівняння (3.39). Отже, система векторів A1, A2, A3 є лінійно залежною, причому розв’язки системи лінійних рівнянь (3.38) є коефіцієнтами лінійної комбінації вектора

00 :0

A1 2A2 A3 0 .

(3.40)

3.8. Характеристичні (власні) корені і власні вектори матриць

Розглянемо систему рівнянь
A X X ,	(3.41)

де — скаляр; А — квадратна матриця порядку n, X — розміром n×1.

Систему (3.41) запишемо у вигляді

A X X 0

або

( A E )X 0.

(3.42)

Остання система n рівнянь з n невідомими має нетривіальний розв’язок, коли

det ( A E ) 0 або	A E	0.	(3.43)

Означення 3.21. Рівняння det ( A E ) 0		відносно	назива-

ють характеристичним рівнянням матриці А.

Корені цього рівняння є характеристичними коренями (характеристичними числами, власними значеннями) матриці А.

Візьмемо будь-який корінь k характеристичного рівняння
(3.43) і підставимо в систему рівнянь (3.42). Дістанемо рівняння
( A E k ) X 0,	(3.44)

яке має нетривіальний розв’язок, оскільки det ( A E ) 0 .

Нехай цим розв’язком є вектор Xk. Такий вектор Xk є характе-

ристичним, або власним вектором матриці А, який відповідає характеристичному кореню k.

Якщо матриця А має n різних характеристичних коренів, то вона має і n різних власних векторів.

Власні вектори визначаються з точністю до множення на скаляр. Це не завжди зручно. Тому часто розглядають нормовані власні вектори, тобто такі, що:

Xi Xi 1 .

Зауважимо, що коли матриця А в рівнянні (3.42) — симетрична (тобто A A ), а Х — матриця, кожний стовпець якої є власним вектором цієї матриці, то добуток

			0	...	0
		01	2	...	0	.	(3.45)
X AX						.	(3.45)
	...		...	...	...
		0	0	...	n

Отже, якщо власні вектори матриці А розміщені у вигляді стов-

пців матриці Х, то добуток X AX дорівнює діагональній матриці,

яка має характеристичні корені на головній діагоналі.

Приклад 3.7. Знайти характеристичні корені матриці А. Запишемо рівняння AX X , або

										a x			a	x		x
										a11 x1			a12 x2			x1
										21 1			22 2					2
			a11x1			a12 x2					x1		0			(a11 x1 ) a12 x2 0													(3.46)
			a		x	a		22	x	2	x	2	0			a		x	(a		22		)x		2	0.			(3.46)
				21 1				22		2		2						21 1			22				2
Запишемо характеристичне рівняння det ( A E ) 0																													для си-
стеми (3.46):
	a11				a12					0 (a11 ) (a22 ) a12a21 0
	a11				a12
	a21				a22
	a21				a22
					2		(a11 a22 ) (a11a22 a12a21 ) 0.																						(3.47)
Отже,
		1,2	1		(a		a			22	)		(a	a	22		)2	4 (a		a		22		a a		21	)	.	(3.48)
		1,2	2			11				22			11		22				11			22		12		21
			2

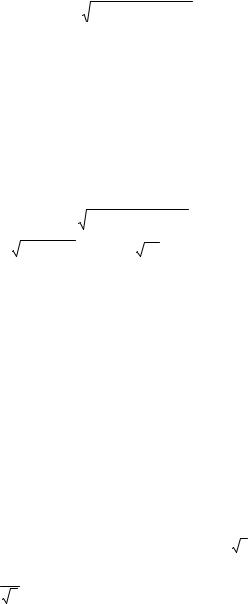
Нехай матриця А — симетрична, тоді a12 a21 і характеристичні корені цієї матриці

1,2	1	(a		a	22	)	(a	a	22	)2 4a2	.	(3.49)
1,2	2		11		22		11		22	12
	2

Підставивши поступово i в систему (3.46), знайдемо власні вектори X1, X2 матриці А.

Приклад 3.8. Знайти характеристичні корені i і власні вектори X1, X2 матриці А:

						A			4		2
						A				2	1	.
										2	1
Матриця А симетрична. Для визначення i застосуємо (3.49):
			1,2	1 (a a			22	) (a a					22		)2	4a2
			1,2		11		22				11		22			12
		1		2							1						1
		1		1)	2	4 2			2		1	(5			25)		1	(5 5);
		(4		1)	3	4 2					2	(5			25)		2	(5 5);
		2									2						2
						1 5;				2 0.
Щоб	знайти			власні		вектори						X1(x11;				x12 )			i X 2 (x21; x22 ) ,
розв’яжемо для кожного i систему рівнянь (3.46).
Нехай i		5 , тоді
(4 5)x11				2x12	0			x11			2x12			0		x11			2x12 . (3.50)
2x		(1 5)x			0				2x		4x			0		x11			2x12 . (3.50)
	11			12						11		12

Нормалізуємо вектор X1 (x11; x12 ) , зводячи його довжину до 1, тобто:

				x112 x122			1 .			(3.51)
Підставимо (3.50) у (3.51):
(2x	)2 x2	4x2	x2		5x2	1	x2	1	x		1	.

12	12	12	12		12		12	5	12	5

Звідси x11 2x12 25 .

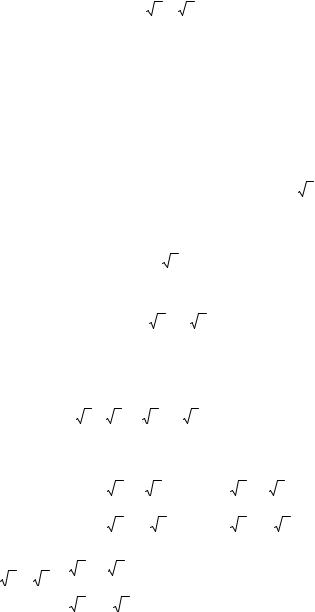
Власний вектор

																		2			1
													X1							;							.														(3.52)
													X1					5		;					5		.														(3.52)
																		5							5
	Для знаходження власного вектора																												X 2 (x21; x22 )										покладемо
2	0 .
	Система (3.46) запишеться у вигляді
								4x		21	2x				22	0				x22									2x21 .												(3.53)
										21					22					x22									2x21 .												(3.53)
								2x21			x22 0
	Нормалізуємо вектор											X 2 (x21; x22 ) ,												звівши його довжину до 1,
тобто:																																1								1
	x212 x222	1 x212 4x212 1 5x212																		1 x212												1			x21					1		. (3.54)
	x212 x222	1 x212 4x212 1 5x212																		1 x212												5			x21					5		. (3.54)
																																5								5
	Підставивши (3.54) у (3.53), дістанемо:
														x22						2			.
	Власний вектор													x22						5			.
																				5

																		1									2														(3.55)
													X 2					1									2
																				;
																		5		;							5		.
																		5									5
	Зауважимо, що оскільки 1																		2	, то власні вектори X1 і X2 ор-
тогональні, тобто лінійно незалежні:
			X1 X 2						2				1				1								2						2				2	0 .
										;									;												5				5
									5	;			5					5	;
									5				5					5								5
	Перевіримо, чи виконується (3.45):
													2					1														2					1
							0															4						2
							0						5					5				4						2					5				5
						1							5					5															5				5
	X AX												1					2														1					2
					0		2																	2				1
					0		2						5											2				1					5					5
													5					5															5					5
									2				1
	10				5													20							5				10				10				5			0
	10				5
									5				5
		5			5				5				5						5						5				5					5
		5			5				1					2					5						5				5					5				0		0	.
		0		0					1					2							0									0								0		0

									5				5
									5				5

Отже, співвідношення		X AX	справді переводить матрицю А в

діагональну матрицю 1		0	. Це підтверджує правильність на-
ведених обчислень.	0	2
ведених обчислень.

3.9.Квадратичні форми

3.9.1.Означення квадратичної форми. Означення 3.22.

Квадратичною формою Q (x1, x2 … xn) від n невідомих x1, x2 … xn

називається сума, кожний доданок якої є квадратом одного з

цих невідомих або добутком двох різних невідомих:

Q(x , x

...x

) a x2

x x

... 2a

x x

...

1 2

11 1

(3.56)

... a22 x22

... 2an2 xn x2

... ann xn2

aij xi x j .

i 1 j 1

Коефіцієнти членів xi2 розміщені на головній діагоналі матри-

ці А, а інші елементи матриці симетричні і дорівнюють відповідно половинам коефіцієнтів за xi xj :

aij

a ji

aij a ji

Симетричну матрицю A (aij

)

називають матрицею квад-

ратичної форми. У векторно-матричній формі квадратична фо-

, де X

(x1, x2 , ... , xn ) , A — симетрична ма-

рма має вигляд X AX

триця.

Розглянемо, наприклад, два випадки.

1. Матриця А має розмір 2×2, а саме

. Тоді квад-

ратична форма

a21

a22

a12 x1 x2

X AX x1

a11 x1

a22

a x x

a x2

x x

x2 .

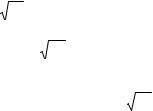
2. Матриця А діагональна, тобто

a11		0		0
A	0	a	22	0	.
	0			a33
		0

У такому разі

				a		0			0		x						a x
	x1	x2	x3		11	a22			0		1		x1 x2			x3	11 1
X AX	x1	x2	x3		0	a22			0		x	2	x1 x2			x3	a22 x2
					0	0
					0	0			a33		x3						a33 x3
					a x			2	a	22	x2	a		33	x2
						11	1			22	2			33	3

— вагова сума квадратів.

Означення 3.23. Квадратичну форму і відповідну їй матрицю А називають додатно визначеною тоді й тільки тоді, коли X AX 0 для всіх дійсних x 0.

Означення 3.24. Квадратичну форму і відповідну їй матрицю називають додатно напіввизначеною, коли X AX 0 для всіх Х.

Запам’ятайте важливу властивість додатно визначених матриць. Матриця А додатно визначена тоді й тільки тоді, коли її харак-

теристичні корені (власні значення) λi додатні, а саме:

			0	...	0
		01	2	...	0	.	(3.57)
X AX						.	(3.57)
	...		...	...	...
		0	0	...	n

Рівняння (3.57) можемо використати для знаходження іншого результату, який корисний для вивчення узагальненого методу найменших квадратів.

Оскільки всі λi додатні, можемо задати діагональну матрицю D такого виду:

		1	0		0 ...	0

		1
			1
		0			0 ...	0
								(3.58)
				2
D					... ...	...	.
	...		...
		0	0		0 ...	1

						n

Неважко побачити, що добуток (3.57) на матрицю D ліворуч і праворуч дає одиничну матрицю:

	(3.59)
XD A XD En .	(3.59)
Нехай Z = XD, тоді	(3.60)
Z AZ En .	(3.60)

Оскільки матриці Х і D — невироджені, то Z — також невироджена. Виконавши відповідні перетворення, дістанемо:

A (Z 1 ) Z 1.

(3.61)

Отже, коли матриця А додатно визначена, то можна знайти таку невироджену матрицю P (Z 1 ) , що A PP .

3.9.2. Випадкові квадратичні форми. Нехай d — випад-

ковий вектор, А — детермінована симетрична матриця.

Добуток d Ad називають випадковою квадратичною фор-

мою, коли коваріаційна матриця d дорівнює cov d у2d E і мате-

матичне сподівання M(d)=0.

Застосувавши оператор математичного сподівання до випад-

кової квадратичної форми d Ad , дістанемо:

M (d Ad) d		tr(A),	(3.62)
	2

де tr(A) — слід матриці А.

Наведемо властивості випадкової квадратичної форми. Нехай d N( , 2 E) :

1. Квадратична форма d Ad має розподіл 2 із k ступенями

свободи, коли А — ідемпотентна матриця (тобто A2 A ) і rgA= =trA=k, якщо 0 , 1 .

2.Нехай В — детермінована матриця, така, що B A=0 і d N( ,2E). Тоді Bd і Ad — незалежні.

3.Якщо A=PP΄ — симетрична матриця, то слід матриці А є сумою її власних значень

i trA .

i 1

4. Усі характеристичні корені ідемпотентної матриці А дорівнюють нулю або одиниці, а саме:

якщо AX X , то A2 X AX 2 X	; проте	A2 X AX X ,
тобто 2 X X , оскільки X 0 , то 2	0 .	Звідси 0 або

1 .

5. Якщо матриця Z має таку властивість, що (Z Z) — квадратна симетрична невироджена матриця rgZ m , то матриця

A En Z Z Z 1 Z є ідемпотентною і rg A n n1 .

		1	1				3
Приклад 3.9. Нехай	Z		2	; тоді	Z		3
Приклад 3.9. Нехай	Z	1	2	; тоді	Z	Z	6
		1	3

Z Z 42 36 6 0 ,

отже, матриця Z Z — невироджена.

		14
Z	1			6	1	;
	1			6	3
	Z		1		3

					6
					6
			5		2		1
			6		6		6
			6		6		6
Z Z Z 1 Z			2		2	2
Z Z Z 1 Z			2		2	2		.
			6		6	6
				1	2	5
				1	2	5
				6	6	6
				6	6	6

6 ;

Визначимо нову матрицю А так:

			1		2	1
			6		6	6
			6		6	6
A En Z(Z Z )	1			2	4		2
A En Z(Z Z )		Z		6	6		6	.
				6	6		6
				1	2		1
				1	2		1
				6	6		6
				6	6		6

Матриця А — симетрична та ідемпотентна, оскільки А2=А. Зауважимо, що ранг матриці А дорівнює 1.

Знайшовши характеристичні корені цієї матриці, тобто розв’язавши рівняння A E 0 , дістанемо 1 =1 і 2 =0, що

ілюструє виконання властивості 4.

3.10. Диференціювання функції багатьох змінних градієнт функції f (x)

Розглянемо операцію диференціювання функції багатьох змінних f(x1, x2... xn), коли змінні задано у формі матриці-рядка, або, що те саме, вектора, тобто X (x1, x2 ... xn ) .

Означення 3.25. Градієнтом функції f(Х) (позначається:

f (x) f (X ) називається вектор, який складається з частин-

(X )

них похідних функції f(x) за x1, x2 ... xn:

		f ( X )
		x1
		x1
	f ( X )	f ( X )
f (x)	f ( X )	x2		(3.63)
	X
	X		.
		...
		f ( X )
		xn
		xn

Нехай потрібно визначити градієнт функції f ( X ) X , коли

( 1, 2 ... n ) і	X (x1, x2 ... xn ) .

Тоді f ( X ) ( 1, 2 ... n ) x...2 1x1 2 x2 ... n xn .

Отже, градієнт функції xn

Узявши до уваги, що			, градієнт можна визначити як
Узявши до уваги, що	X X		, градієнт можна визначити як
( X )	( X ) ( 1, 2 ... n ) .			(3.65)

X		X

Далі розглянемо функцію f (X ) X AX , де A=(aij) — симетрична матриця порядку n і X (x1, x2 ... xn ) — n-вимірна матриця-

стовпець. Функцію такого типу визначають як квадратичну форму (див. підрозд. 3.9).

Визначимо градієнт квадратичної форми. Для цього подамо f ( X ) X AX як скалярний добуток:

						a	a	...
						a1121	a1222 ...
	x	x		... x
X AX	x	x		... x	n
	1		2		n	... ... ...
						an1	an2 ...

a	x
a	1n 1
a	2n x2
... ...
ann xn

(a11x1 a21x2 ...

an1xn ;

a12 x1 a22 x2 ...

an2 xn ...

... a1n x1 a2n x2 ... ann xn ) x2 (3.66)

...

x1(a11x1

a21x2 ... an1xn ) x2 (a12 x1 a22 x2

... an2 xn )

... xn (a1n x1

a2n x2 ... ann xn ) .

Знайдемо компоненти вектора-градієнта.

Перший компонент:

f X

... a

X AX 2a

2a12

2a1n

2a11x1 2a12 x2 ... 2a1n xn 2 a1 j x j .

j 1

Другий компонент:

( X AX )

2a21x1 2a22 x2

2a23 x3

... 2a2n xn 2

a2 j x j .

j 1

<<< < Предыдущая 1 2 3 4 5 6 78 / 558 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Моделирование

#
28.01.20224.3 Mб10cgiirbis_64 (6).pdf
#
28.01.20224.3 Mб3cgiirbis_64 (7).pdf
#
28.01.20224.46 Mб32Econometrics.pdf
#
18.12.202180.65 Кб42індивідуальна робота.xlsx
#
28.01.20229.75 Mб31все пм тести решения.docx
#
18.12.20212.39 Mб6звіт лр1.docx
#
18.12.20212.8 Mб7звіт лр2.docx
#
18.12.20212.49 Mб5звіт лр3.docx