Econometrics

Таблиця 11.6

28

Середнє значення випуску гранульованого фосфату становить yt 126711 115,18 .

Середній квадрат відхилень фактичних значень випуску продукції від вирівняних за експонентою подається так:

u2 5411,69 4,97,

а середнє квадратичне відхилення буде σu= 4,97 =2,23. Таким чином, коефіцієнт варіації

( u / yt ) 100 (2,23/115,18) 100 % 1,9 %.

Звідси маємо, що розраховану криву зростання

ŷt=110,04 100,0406t=110,04(1+0,098)t

дістанемо з досить високою точністю, бо коефіцієнт варіації менший ніж5%.

11.5.4. Оцінка адекватності й точності трендових моделей. Незалежно від того, яким способом вибрано функцію зростання і розраховано її параметри, питання про можливість її застосування для аналізу і прогнозування того чи іншого економічного явища може бути розв’язане тільки після встановлення її адекватності, тобто встановлення відповідності розрахованої моделі досліджуваному об’єктові чи процесу.

Звичайно, адекватність розглядається не взагалі, а саме за тими властивостями моделі, що їх дослідник вважає істотними. Трендова модель ŷt конкретного часового ряду yt буде адекватною, якщо вона правильно відбиває систематичні компоненти ча-

29

сового ряду. Ця вимога еквівалентна тому, щоб залишки ut=yt– ŷt(t=1,n) задовольняли властивостям випадкової складової часового ряду, котрі наводились в розділі 4 (див. підрозд. 4.3), а саме:

випадковість коливань послідовності залишків і відповідність їх нормальному законові розподілу; рівність нулю математичного сподівання; незалежність значень їхніх рівнів.

Розглянемо перевірку деяких основних властивостей випадкової складової часового ряду.

11.5.4.1. Перевірка випадковості коливань рівнів послідо-

вності залишків. Ця перевірка має бути проведена передусім для підтвердження гіпотези про достовірність вибору виду тренду.

Для дослідження випадковості відхилень від тренду нам потрібно розрахувати послідовність залишків ut = yt – ŷt (t = 1, n).

Характер цих відхилень вивчається за допомогою низки критеріїв. Одним з них є метод серій, що ґрунтується на медіані вибірки.

Алгоритм методу серій:

Крок 1.

Ряд залишків ut ранжується в порядку зростання (або спадання) і знаходиться медіана uмe = u(n+1)/2, коли n — непарне,

і uмe = (un/2 + u(n/2) + 1)/2, коли n — парне.

Крок 2.

Повертаючись до початкової послідовності залишків (перед ранжуванням їх), кожне значення порівнюється з медіаною uмe:

якщо ut > uмe, то ставиться знак «+»; якщо ut < uмe, то ставиться знак «–»;

якщо ut = uмe, відповідне значення ut не враховується. Утворюється послідовність, що складається з плюсів і мінусів.

Означення. Послідовність плюсів або мінусів, що йдуть підряд, має назву серії.

Примітка:

Якщо є один плюс (мінус), що чергується з мінусом (плюсом), то його потрібно вважати окремою серією.

Крок 3.

Визначається загальна кількість серій V і найбільша протяжність однієї з серій kmax.

Для того, щоб послідовність залишків мала випадковий характер, kmax не може бути досить великою, а кількість серій — не досить малою.

30

Крок 4.

Для 5%-го рівня значущості розраховуються дві нерівності, що мають виконуватись одночасно:

kmax < [3,3 (lgn +1)];

V > [1/2(n + 1 – 1,96 n 1 )],

де квадратні дужки визначають цілу частину числа.

Якщо хоча б одна нерівність порушується, то гіпотеза про випадковий характер залишків часового ряду відхиляється і, відповідно, трендова модель (крива зростання) є неадекватною.

Іншим критерієм, який досить часто застосовується для перевір-

ки випадковостізалишків, є критерійпіків(поворотнихточок).

Сутність його полягає в такому.

Крок 1.

У послідовності залишків вибираються поворотні точки.

Означення. Поворотною точкою є значення рівня залишків, що більше (менше) від обох сусідніх рівнів, тобто

ut–1 < ut > ut+1, або ut–1 > ut < ut+1.

Крок 2.

Визначається загальна кількість поворотних точок П.

Крок 3.

Обчислюється математичне сподівання поворотних точок і їх дисперсія 2п за умови випадкової вибірки залишків:

= 2/3(n – 2); 2п = (16n – 29)/90.

Крок 4.

Критерієм випадковості залишків з 5%-м рівнем значущості має бути виконання нерівності

де квадратні дужки тут теж означають цілу частину числа. Якщо ця нерівність не виконується, трендова модель вважається неаде-

кватною.

11.5.4.2. Перевірка відповідності розподілу випадкової компоненти нормальному закону. Ця перевірка може бути проведена лише наближено за допомогою дослідження показників асиметрії γ1 і ексцесу γ2.

31

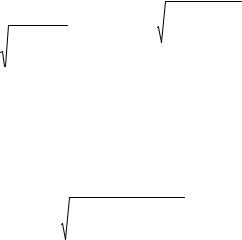
Для нормального закону розподілу ці показники в генеральній сукупності дорівнюють нулю.

Припускаємо, що відхилення від тренду є вибіркою з генеральної сукупності.

Обчислимо вибіркові значення асиметрії та ексцесу і їхні похибки.

Вибіркова асиметрія €1 і її похибка € 1 дорівнює:

то гіпотеза про нормальний розподіл випадкових залишків приймається і модель вважається адекватною.

Якщо виконується хоча б одна нерівність

то гіпотеза про нормальний закон розподілу випадкової компоненти ut відхиляється і модель вважається неадекватною.

Крім розглянутих методів відома ще ціла низка інших методів: метод Вестергарда, RS-критерій і т. ін.

Найбільш простий з них RS-метод полягає в наступному.

32

Розраховуємо величину розмаху R між рівнями ряду залишків

Тоді розрахункове значення величини RS дорівнює відношен-

ню RS = R/S.

Розраховане значення величини RS порівнюється з табличним RS-критерієм (а саме, з його нижньою і верхньою межею для рівня значущості ). Якщо ці значення не потрапляють в інтервал між критичними (табличними) межами, то гіпотеза про нормальний закон випадкової складової відхиляється.

Наведемо декілька табличних значень меж RS-критерію (для

= 0,05):

для n = 10 нижня межа: 2,67; верхня межа: 3,685; для n = 20 нижня межа: 3,18; верхня межа: 4,49; для n = 30 нижня межа: 3,47; верхня межа: 4,849.

11.5.4.3. Перевірка рівності нулю математичного сподівання випадкової складової. Ця перевірка має бути тоді, коли ряд залишків εt підпорядкований нормальному закону розподілу. Розраховуємо значення tp за формулою:

tp ut 0 n ,

u

де ut — середнє значення рівнів залишків, σu — середнє квадратичне відхилення залишків.

Якщо розрахункове значення tp менше табличного t для рівня значущості і ступенів свободи n–1, тобто tp < t , то гіпотеза про рівність нулю математичного сподівання випадкової складової приймається; у протилежному випадку — відхиляється.

Перевірка незалежності значень рівнів залишків відбуваєть-

ся за критерієм Дарбіна—Уотсона, фон Неймана і т. ін. (див. під-

розд. 8.2).

11.5.4.4. Розрахунок точності трендових моделей. Ви-

сновок про адекватність трендової моделі робиться тоді, коли всі попередні перевірки властивостей залишків дають позитивні результати.

Для адекватних моделей повинно бути поставлене питання про точність моделі.

Точність характеризується величиною відхилень значень рівнів ряду за кривою зростання від фактичного рівня. Далі наведе-

33

мо кілька показників, які можна застосувати як статистичні показники точності моделі.

Середнє квадратичне відхилення

де n — кількість рівнів ряду; m — кількість параметрів, що має функція зростання; yt — фактичний рівень ряду; ŷt — значення рівня ряду за трендовою моделлю.

Середня відносна похибка апроксимації

Коефіцієнт збіжності

Коефіцієнт детермінації R2 = 1 – φ2 і т. ін.

За цими показниками можна зробити вибір із декількох трендових моделей і обрати найбільш точну. Слід зауважити, що можуть бути випадки, коли за деякими показниками буде точна одна з моделей, а за другими — інша. Тоді потрібні додаткові дослідження і уточнення моделі.

Приклад 11.7. Для часового ряду, що описує динаміку фірми за дев’ять років, розрахована трендова модель лінійного типу

ŷt=87,8–3,4t.

Потрібно оцінити адекватність і точність побудованої моделі. У табл. 11.7 наведені вихідні дані й відповідні величини, що

необхідні для розв’язання задачі.

1. Перевірка випадковості залишків.

Скористаємося критерієм поворотних точок.

З табл. 11.7 бачимо (графу 5), що в даному ряду є шість піків, тобто П=6.

Розрахуємо:

34

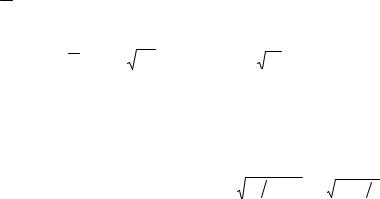
= 2/3(9 –2) = 14/3; σ2п = (16 × 9 – 29) / 90 = 115/90 ≈ 1,3.

Обчислимо цілу частину виразу:

[ – 1,96 2 ] = [14/3 – 1,96 1,3 ] = 2.

Отже, видно, що П > 2 (тобто 6 > 2), і робимо висновок, що з імовірністю 0,95 випадковість залишків підтверджується.

=0,05; НМ=2,7 і ВМ=3,7). Доходимо висновку, що властивість нормального розподілу залишків виконується.

3. Перевірка наближення до нуля математичного споді-

вання ряду залишків.

За результатами обчислення з табл. 11.7 (графа) середнє значення залишків дорівнює (–0,3) : 9 ≈ –0,03 і, отже, можна підтвердити виконання цієї властивості без застосування критерію Стьюдента.

4. Перевірка незалежності рівнів ряду залишків.

Скористаємось критерієм Дарбіна—Уотсона

Розрахунки за цією формулою наведені в таблиці 11.7 (результати графи 8: результати графи 6). Згідно з цим

DW=35,26/15,51=2,27.

Ця величина більша 2, що відповідає від’ємній автокореляції. Перетворимо критерій Дарбіна—Уотсона DW =4–DW=4– 2,27=1,78.

Це значення порівнюється з двома критичними табличними рівнями

36

DW1=1,08 і DW2=1,36.

Розраховане значення DW = 1,78 більше від табличного верхнього рівня критерію Дарбіна—Уотсона, і потрапляє в проміжок від DW2 до 2, тобто 1,78>1,36, звідки зробимо висновок про незалежність рівнів послідовності залишків.

Отже, послідовність залишків задовольняє усі властивості випадкового компонента часового ряду, і тому побудовану модель ŷ=87,8–3,4t вважаємо адекватною.

Для характеристики точності трендової моделі розрахуємо показник середньої відносної похибки (див. табл. 11.7, графа 9):

εвідн.=13,29:9=1,48%.

Ця похибка не перевищує 5%, що відповідає достатній точності побудованої трендової моделі.

11.6. Прогнозування економічної динаміки за трендовими моделями

Головною метою дослідження трендових моделей економічної динаміки є розрахунок прогнозів про розвиток досліджуваного процесу.

Прогнозування часового ряду ґрунтується на методі екстраполяції, тобто, спостерігаючи ту чи іншу тенденцію зміни процесу в минулому, продовжуємо її з певною ймовірністю у майбутній період. Згідно з цим припускається, що прогнозуючий економічний показник формується під упливом великої кількості факторів, визначити кожний з яких або неможливо, або відсутня кількісна інформація про їхній рівень.

У цьому випадку зміну тенденції певного економічного показника пов’язують не з факторами, а з плином часу, що відбивається на рівнях часового ряду. Застосування методу екстраполяції, використовуючи криві зростання, базується на двох припущеннях:

часовий ряд справді має тренд;

тенденція, що виявлена в минулому періоді, не буде мати суттєвих змін у майбутньому.

Процес екстраполяційного прогнозування економічної динаміки за трендовими моделями складається з таких етапів:

попередній аналіз даних;

37