Econometrics

Знайдіть розв’язок даної системи рівнянь.

19.Яка матриця називається блочною?

20.Задано по чотири блоки блочних матриць А і В:

89

Знайдіть суму (різницю) блочних матриць A B .

21.Яка умова множення блочних матриць? З відповідних блоків матриць А і В з попереднього завдання складіть дві матриці, які можна було б помножити одна на одну.

22.Задано матриці

Знайдіть матрицю Кронеккeр-добутку (прямого множення) A B . 23. Задано блочну невироджену матрицю

Знайдіть обернену матрицю A 1 .

24.Яке рівняння має назву характеристичного рівняння матриці А?

25.Яку назву мають корені характеристичного рівняння?

26.Чомудорівнюєдобуток X AX , де Х— власнівектори матриці А?

27.Знайдіть характеристичні корені й власні вектори матриці:

28. Дайте означення квадратичної форми. Запишіть її у розгорнутому вигляді й у матричній формі.

29. Коли квадратична форма є додатно визначеною і напіввизначеною?

30.Яка квадратична форма має назву випадкової квадратичної форми?

31.Чому дорівнює математичне сподівання випадкової квадратичної форми?

32. Сформулюйте властивості випадкової квадратичної форми.

3.13. Основні терміни і поняття

90

Матриця Прямокутна матриця Квадратна матриця Транспонована матриця Діагональна матриця Симетрична матриця Одинична матриця Матриця-стовпець Матрицярядок Ідемпотентна матриця Ранг матриці Слід матриці Детермінант (визначник) Скаляр Мінор Алгебраїчне доповнення Кронеккерове (пряме) множення матриць Приєднана матриця Обернена матриця Блочна матриця Характеристичне рівняння Характеристичні корені Власні вектори матриці Квадратична форма Випадкова форма

91

Розділ 4

МЕТОДИ ПОБУДОВИ ЗАГАЛЬНОЇ ЛІНІЙНОЇ МОДЕЛІ

4.1. Поняття моделі та етапи її побудови

Перша принципова задача, з якою стикається кожний, хто вивчає економіку, — це задача про встановлення взаємозв’язків між економічними величинами. Так, попит на деякий товар, що формується на ринку, залежить від ціни цього товару та ціни конкуруючих товарів, споживчого доходу і т.ін. Витрати, що пов’язані з виготовленням будь-якої продукції, залежать від обсягу виробництва, технології, зовнішніх і внутрішніх умов, від цін на основні виробничі ресурси. Можна було б навести ще багато прикладів про взаємозв’язки між економічними показниками. Адже вони не є ізольованими, автономними, а мають між собою прямі і зворотні зв’язки. Звідси, щоб ефективно керувати економічними процесами та явищами, треба вміти вимірювати ці зв’язки кількісно.

Цю проблему економіки можна вирішити, побудувавши економетричну модель.

Означення 4.1. Економетрична модель — це функція чи си-

стема функцій, що кількісно описує залежність між соціальноекономічними показниками, один чи кілька з яких є залежною змінною, інші — незалежними.

У загальному вигляді економетрична модель запишеться так:

Y f ( X1, X 2 , X 3 ... X m 1, u) ,

де Y — залежна змінна; Xj ( j 1, m 1) — незалежні змінні; u — стохастична складова, або на основі системи рівнянь:

Ys f ( X s1, X s2 , X s3 ... X sm 1 us ) ,

де us — стохастична складова s-го рівняння, s 1, k

економетрична модель складається з k функцій.

Незалежні змінні моделі називаються пояснювальними, наперед заданими змінними. Залежні змінні називаються пояснюваними змінними.

91

Економетрична модель, що будується на основі системи рівнянь, крім регресійних функцій, може містити тотожності.

Побудова будь-якої економетричної моделі, незалежно від того, на якому рівні і для яких показників вона будується, здійснюється як послідовність певних кроків.

Крок 1.Знайомство з економічною теорією, висунення гіпотези взаємозв’язку. Чітка постановка задачі.

Крок2.Специфікація моделі. Використовуючи всі ті види функцій, які можуть бути застосовані для вивчення взаємозв’язків, необхідно сформулювати теоретичні уявлення і прийняті гіпотези у вигляді математичних рівнянь. Ці рівняння встановлюють зв’язки між основними визначальними змінними, припускаючи, що решта змінних є випадковими.

Крок 3. Формування масивів вихідної інформації згідно з метою та завданнями дослідження.

Крок 4. Оцінка параметрів економетричної моделі методом найменших квадратів. Аналіз залишків дає змогу відповісти на запитання: чи несуперечить специфікаціямоделізастосуванню 1МНК.

Крок 5. Якщо деякі передумови застосування 1МНК не виконуються, то для подальшого аналізу треба замінювати специфікацію або застосовувати інші методи оцінювання параметрів.

Крок 6. Верифікація моделі та її оцінок параметрів. Крок 7. Прогноз на основі моделі.

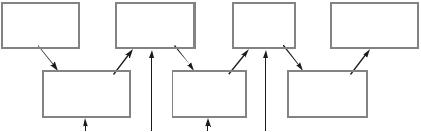
Схематично всі кроки можна зобразити так:

Рис. 4.1. Етапи побудови моделі

4.2. Специфікація моделі

Економетрична модель базується на єдності двох аспектів — теоретичного, якісного аналізу взаємозв’язків та емпіричної ін-

92

формації. Теоретична інформація знаходить своє відображення у специфікації моделі.

Специфікація моделі — це аналітична форма економетричної моделі на основі досліджуваних чинників. Вона складається з певного виду функції чи функцій, що використовуються для побудови моделей, має ймовірнісні характеристики, які притаманні стохастичним залишкам моделі.

З досвіду економетричних досліджень, а також на підставі якісного теоретичного аналізу взаємозв’язків між економічними показниками, можна навести клас функцій, які можуть описувати ці взаємозв’язки:

1) лінійна функція:

ya0 a1x1 a2 x2 ... am xm ;

2)степенева функція:

де t j x2j .

У цих функціях:

y — залежна (пояснювана) змінна;

x j , j 1, m 1 — незалежні, або пояснювальні, змінні;

a j , j 0, m — параметри функцій.

Серед наведених видів функцій три останні є нелінійними. Але за допомогою перетворення залежної і незалежних змінних ці функції можна звести до лінійного виду.

Лінійні функції найпоширеніші в економетричному моделюванні, тому обґрунтування економетричних методів розглянемо на базі лінійних моделей.

93

Маючи на увазі, що вибір аналітичної форми економетричної моделі не може розглядатись без конкретного переліку незалеж-

них змінних, специфікація моделі передбачає добір чинників для

економетричного дослідження.

При цьому в процесі такого дослідження можна кілька разів повертатись до етапу специфікації моделі, уточнюючи перелік незалежних змінних та вид функції, що застосовується. Адже коли вид функції та її складові не відповідають реальним процесам, то йдеться про похибки специфікації.

Похибки специфікації моделі можуть бути трьох видів: 1)ігнорування при побудові економетричної моделі істотної

пояснювальної змінної; 2)введення в модель незалежної змінної, яка не є істотною для

вимірюваного зв’язку; 3) використання не відповідних математичних форм залежності.

Перша з цих помилок призводить до зміщення оцінок, причому зміщення буде тим більшим, чим більша кореляція між введеними та не введеними до моделі змінними, а напрям зміщення залежить від знака оцінок параметрів при введених змінних і від характеру кореляції між введеними та навіть не введеними змінними. Оцінки параметрів також будуть зміщеними (в цьому випадку вони вищі), тому застосування способів перевірки їх значущості може призвести до хибних висновків щодо значень параметрів генеральної сукупності.

Для відшукання цього джерела помилок специфікації досить важко запропонувати будь-які загальні міркування, оскільки незалежна змінна, що не враховується (або незалежні змінні), може бути одним із багатьох можливих пояснень. Про необхідність введення до моделі цих незалежних змінних можна лише здогадуватись на підставі апріорних міркувань. Проте відомі й більш формалізовані процедури, які дають змогу з’ясувати, наскільки істотним є введення до моделі будь-якої змінної. Так, наприклад, якщо побудувати економетричну модель на базі покрокової регресії (метод покрокової регресії розглянемо пізніше), то можна досить чітко ранжувати пояснювальні змінні за величиною їх впливу на залежну змінну. Про відсутність основної змінної свідчить зміна поведінки випадкового відхилення у помилково специфікованій моделі.

Друга помилка специфікації. У випадку, коли до моделі вводиться змінна, яка неістотно впливає на залежну змінну, то (на відміну від першої помилки специфікації) оцінки параметрів моделі будуть незміщеними. При цьому за допомогою звичай-

94

них процедур можна дістати також незміщені оцінки дисперсій цих параметрів. Проте це не означає, що економетричну модель можна беззастережно розширювати за рахунок «неістотних» змінних. Адже існує ненульова ймовірність того, що в результаті використання вибіркових даних змінна, яка зовсім не стосується моделі, покаже істотний зв’язок із залежною змінною. А це означає, що кількісний зв’язок між змінними буде виміряно неправильно.

Третя помилка специфікації. Припускається, що залежна змінна є лінійною функцією від деякої пояснювальної змінної, анасправді йдеться про квадратичну, кубічну чи якусь поліноміальну залежність вищого порядку. У цьому разі наслідки такі самі, як і за першої помилки специфікації: оцінки параметрів моделі матимуть зміщення.

Питання про вибір найкращої форми залежності має базуватися на перевірці ступеня узгодженості виду функції з вихідними даними спостережень.

Адекватність побудованої моделі можна встановити, проаналізувавши залишки моделі. Вони обчислюються як різниця між фактичними значеннями залежної змінної і розрахованими за моделлю. Щоб перевірити, чи має розподіл залишків невипадковий характер, можна скористатися критерієм Дарбіна—Уотсона. Тоді перевірка моделі на існування автокореляції першого порядку аналогічна перевірці того, наскільки вдало вибрано форму економетричної моделі.

4.3. Передумови застосування методу найменших квадратів (1МНК)

Нехай економетрична модель у матричній формі має вигляд

де Y — вектор значень залежної змінної; X — матриця пояснювальних змінних розміром n m (n — кількість спостережень, m — кількість змінних); A — вектор параметрів моделі; u — вектор залишків.

Застосовуємо 1МНК для оцінювання параметрів моделі, якщо виконуються наведені далі умови.

1) Математичне сподівання залишків дорівнює нулю:

95

3) пояснювальні змінні моделі не пов’язані із залишками:

4) пояснювальні змінні моделі утворюють лінійно незалежну систему векторів, або, іншими словами, пояснювальні змінні не повинні бути мультиколінеарними, тобто матриця Х має повний ранг.

Перша умова, здавалося б, є очевидною. Адже коли математичне сподівання залишків не дорівнює нулю, то це означає, що існує систематичний вплив на залежну змінну і до модельної специфікації не введено всіх основних пояснювальних змінних. Якщо ця передумова не виконується, то йдеться про помилку специфікації.

Друга умова передбачає наявність сталої дисперсії залишків та відсутність кореляції між ними. Наявність сталої дисперсії називають гомоскедастичністю. Проте вона може виконуватись лише тоді, коли залишки u є похибками вимірювання. Якщо залишки акумулюють загальний вплив змінних, які не враховано в моделі, то звичайно дисперсія залишків не може бути сталою величиною, вона змінюється для окремих груп спостережень. У такому разі йдеться про явище гетероскедастичності, яке впливає на методи оцінювання параметрів. Якщо між залишками існує залежність (автокореляція), то вона також впливає на методи оцінювання параметрів.

Третя умова передбачає незалежність між залишками і пояснювальними змінними, яка порушується насамперед тоді, коли економетрична модель будується на базі одночасних структурних рівнянь або має лагові змінні. Тоді для оцінювання параметрів моделі використовується, як правило, двоабо трикроковий методи найменших квадратів.

Четверта умова означає, що всі пояснювальні змінні, які входять до економетричної моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже важко вирізнити такий масив пояснювальних змінних, які були б зовсім не пов’язані

96

між собою. Тоді щоразу необхідно з’ясовувати, чи не впливатиме залежність пояснювальних змінних на оцінку параметрів моделі.

Це явище називають мультиколінеарністю змінних, що призводить до ненадійності оцінки параметрів моделі, підвищує їхню чутливість до вибраної специфікації моделі та до конкретного набору даних. Знижується рівень довіри до результатів верифікації моделей за допомогою 1МНК. Отже, це явище з усіх поглядів є, звичайно, небажаним. Але воно досить поширене, тому методи виявлення мультиколінеарності й способи її врахування за допомогою специфікації моделі чи спеціальних методів оцінювання параметрів є важливою економетричною проблемою.

4.4. Оператор оцінювання 1МНК

Оцінимо методом 1МНК параметри моделі (4.1), для якої виконуються чотири розглянуті щойно умови.

Рівняння (4.1) подамо у вигляді: u Y XA . Тоді суму квадратів залишків u можна записати так:

або

X — матриця, транспонована щодо матриці пояснювальних змінних X.

Звідси

Рівняння (4.6) дає матричну форму запису системи нормаль-

них рівнянь, а формула (4.7) показує, що вектор € є розв’язком

системи таких рівнянь.

A

Формули (4.6) і (4.7) можна дістати й інакше.

Так, помноживши рівняння (4.1) зліва спочатку на X , а потім на матрицю ( X X ) 1, дістанемо:

97