12_Uravnenie_dinamiki_vraschatelnogo_dvizhenia_Moment_sily_moment_inertsii

Уравнение динамики вращательного движения. Момент силы, момент инерции.

В торой закон Ньютона для вращательного движения выглядит следующим образом:

П о определению угловое ускорение и тогда это уравнение можно переписать следующим образом:

Уравнение динамики вращательного движения записывается так: M = dL/dt, так как Li = Iiω.

О сновное уравнение динамики вращательного движения формулируется следующим образом: изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.

Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.

В скалярной форме: Mi = ri*Fi*sin(ri, Fi).

Считая, что ri*sinα = li, то Mi = liFi.

Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.

Уравнение динамики вращательного движения записывается так: M = dL/dt.

Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой L = mi*υi*ri.

Если вместо линейной скорости подставить ее выражение через угловую: υi = ωri, то выражение для момента импульса примет вид Li = mi*ri*2ω.

Величина Ii = mi*ri^2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем: Li = Iiω.

Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело: L = Iω.

Закон вращательного движения гласит: M = dL/dt.

Известно, что представить момент импульса тела можно через момент инерции: L = Iω.

Тогда: M = Idω/dt.

Учитывая, что угловое ускорение определяется выражением ε = dω/dt, получим формулу для момента силы, представленного через момент инерции: M = Iε.

Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси: J = m(r^2).

М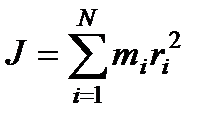 омент инерции системы материальных точек будет равен сумме моментов инерции отдельных точек.

Е сли масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.

В результате получается следующее выражение:

Д ля однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде: dm = ρdv, преобразуем формулу следующим образом:

Размерность момента инерции – кг*(м^2).

Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.

Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.

В сякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое.

М омент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:

Момент инерции шара радиуса R:

М омент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:

М омент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:

М омент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.