
УМК МЖГ стр 76-157 Модуль 4-7_МЖГ
.pdf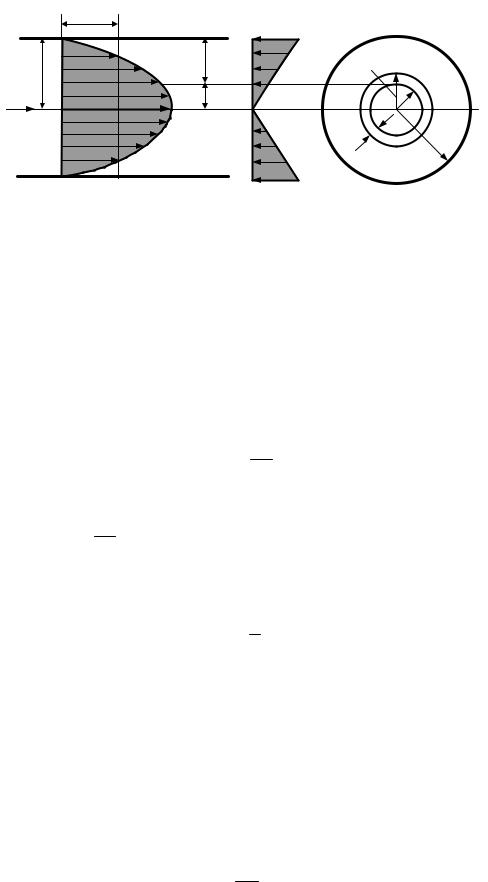
0
При равномерном ламинарном движении жидкости в трубе:
ux = u; ur = 0 .
Движение можно представить как совокупность бесконечно тонких коль- цевых концентрических слоев, перемещающихся относительно друг друга.
Возникающие между слоями жидкости касательные напряжения по Ньютону:
t = -m du . dr
С ростом r (от оси к стенке трубы) скорость и уменьшается, поэтому
градиент скорости du < 0 . Поскольку касательное напряжение t – величи- dr
на положительная, вводится знак минус.
Для касательного напряжения ранее было получено соотношение:
t = rg r J , 2
где J – гидравлический уклон. Тогда получим:
|
rg |
r |
J = -m |
du |
, |
|
|
|
|
|
|
||||
|
2 |
|
dr |
||||
откуда |
du = - ρgJ r dr = - |
gJ |
r dr , |
||||
|
|||||||
|
2m |
|
|
2n |
|||
Полагая, что n не изменяется в пределах живого сечения [n ¹ f(r)], и учитывая, что J не зависит от r, получаем:
∫du = - 2gJn ∫r dr .
136
После интегрирования:
u = - |
gJ |
r2 + C . |
|
|||||
|
|
|
||||||
|
|
4n |
|
|
||||
Находим постоянную интегрирования С из условия «прилипания» |
||||||||
жидкости к стенке. При r = r0 скорость и = 0, поэтому: |
|
|||||||
C = |
|
gJ |
|
× r2 . |
|
|||
|
4n |
|
||||||
|
|
|
|
0 |
|
|||
Тогда для местной скорости в точке живого сечения, расположенной |
||||||||
на расстоянии r от оси трубы, имеем: |
|
|
||||||
u = |
gJ |
|
(r 2 |
- r2 ) . |
(7.6) |
|||
4n |
|
|||||||
|
0 |
|
|
|
||||
Таким образом, при ламинарном движении жидкости в цилиндриче- ской трубе круглого сечения (напорный поток) распределение местных скоростей по радиусу имеет параболический характер (рис. 7.6). Плоская эпюра скорости – парабола.
Из (7.6) следует, что максимальная скорость имеет место на оси тру-
бы, то есть при r = 0: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
= |
gJ |
|
r 2 . |
|
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
max |
|
4n |
0 |
|
|
|
|
|
||||
Выразим местную скорость u через umax: |
|
|||||||||||||
|
|
|
|
|
|
r |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
u = umax |
1 - |
|
|
|
|
. |
(7.7) |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
r0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Безразмерная местная скорость: |
|
|
|
|
|
|
|
|
|
|||||
|
u |
=1 - |
|
r |
2 |
. |
(7.8) |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
umax |
|
|
|
|
|||||||||
|
|
|
|
r0 |
|
|
|
|
||||||
Следовательно, эпюры безразмерных местных скоростей при лами- нарном движении жидкости в трубах одинаковы и их можно представить параболой (рис. 7.6).
Расход. Для определения расхода в одном из поперечных сечений трубы выделим на расстоянии r от оси трубы элементарную площадку в виде кольца толщиной dr (рис. 7.6). Площадь кольца dω = 2πr dr . Расход через площадку определится по соотношению dQ = u2πrdr . Расход через сечение:
r0 r0
Q = ∫ u dw = 2p ∫ ur dr .
0 |
0 |
|
137 |

Подставив значение и из (7.7) и помня замечание о независимости ν от r, получим:
Q = |
2πumax |
∫(r02 − r2 )r dr = πr02 |
umax |
|||
r02 |
||||||
|
|
πgJ |
2 |
|
||
или |
Q = |
d 4 |
|
|||
|
|
|||||
|
|
128ν |
|
|
||
Важно отметить, что при заданном J расход в трубе в условиях напор- ного ламинарного движения пропорционален четвертой степени диаметра.
Средняя скорость. Учитывая, что υ = Q / ω, найдем выражение для
средней скорости: |
|
|
|
|
|
υ = |
gJ |
d 2 = |
gJ |
r2 . |
(7.9) |
32ν |
|
||||
|
|
8ν 0 |
|
||
Сравнивая формулы для umax и υ, видим, что:
υ = 0,5 umax,
т.е. средняя скорость в сечении напорного ламинарного потока в цилинд- рической трубе круглого сечения равна половине максимальной скорости.
Коэффициент кинетической энергии равен:
|
|
|
|
|
|
|
r0 |
|
gJ |
(r2 |
|
− r 2 ) |
3 |
2πr dr |
|
||||||
|
|
|
|
|
3 |
|
∫ |
|
|
|
|
||||||||||
|
1 |
u |
|
|
4ν |
0 |
|
|
|
|
|
|
|||||||||
α = |
|
dω = |
0 |
|
|
|
|
|
|
|
|
= 2 . |
|||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
gJr2 3 |
|||||||||||
|
ω ω |
υ |
|
|
|
|
|
πr |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
8ν |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Градиент местной скорости |
|
|
du |
= − |
gJ |
r , то есть изменяется прямо |
|||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dr |
|
|
2ν |
|
|
|
|
||||
пропорционально расстоянию r данной точки (данного слоя) от оси трубы.
Градиент du < 0 . dr
Касательные напряжения линейно увеличиваются от нуля на оси
трубы до τ0 |
= ρg |
r0 |
J на стенке (рис. 7.6). |
|
|
|
|||||
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
Действительно, τ = −μ |
du |
, a |
du |
= − |
gJ |
r , откуда τ = ρg |
r |
J |
|||
|
|
2ν |
|
||||||||
|
|
|
|
dr dr |
|
2 |
|
||||
138

3.2.Коэффициент Дарси при ламинарном напорном движении
втрубе
Из (7.9) можно записать выражение для гидравлического уклона:
J = |
hдл |
= |
32νυ |
. |
|
||
|
|
|
|
|
|||
|
l |
|
gd 2 |
|
|||
Тогда имеем |
|
|
|
|
|
||
h = |
32νlυ |
. |
(7.10) |
||||
|
|||||||
дл |
gd 2 |
|
|||||
|
|
|
|
||||
Зависимость (7.10) определяющая величину потерь напора при ла- минарном режиме движения, показывает, что потери напора при ламинар-
ном режиме пропорциональны первой степени средней скорости зависят от рода жидкости, обратно пропорциональны площади сечения трубы и не зависят от шероховатости стенок трубы.
Учитывая, что общее выражение для потерь напора по длине труб определяется по формуле Дарси – Вейсбаха:
|
|
= l |
|
l |
× |
u2 |
|
|||
|
h |
|
|
|
|
, |
(7.11) |
|||
|
|
|
|
|||||||
|
дл |
|
d |
|
2g |
|
||||
|
|
|
|
|
|
|
||||
приравняв его к (7.10), получим: |
|
|
|
|
|
|
|
|
|
|
|
lu2 |
32nu |
|
|
|
|||||
|
|
|
= |
|
|
|
|
. |
|
|
|
d × |
|
|
|
|
2 |
|
|||
|
2g |
|
gd |
|
|
|
||||
Отсюда коэффициент Дарси (коэффициент гидравлического трения):
l = 64ν , ud
или |
l = |
64 |
. |
||
|
|||||
|
|
|
Re |
||
|
Если выразить число Re через гидравлический радиус R, то: |
||||
|
l = |
16 |
|
||
|
ReR |
||||
|
|
||||
|
Потери напора по длине трубы круглого сечения при равномерном |
||||
ламинарном движении пропорциональны средней скорости потока в пер-
вой степени. Это следует из (7.11), если подставить в эту формулу l = 64 × n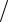 (u × d ) , и из (7.10). Опытные данные подтверждают установлен- ную зависимость hдл от u в первой степени.
(u × d ) , и из (7.10). Опытные данные подтверждают установлен- ную зависимость hдл от u в первой степени.
139

Б. Турбулентный режим движения 3.3. Логарифмический закон распределения осредненных скоро-
стей в турбулентном потоке
Рассмотрим плоское равномерное турбулентное движение вдоль твердой границы, в системе координат х, у, z. Направление оси ОХ совпа- дает с направлением линий тока осредненного движения, которые пред- ставляют собой параллельные прямые. Тогда ux = ux ( z ); uy = 0; uz = 0
(см. модуль 5, п. 2), где z – расстояние данной точки от стенки по нормали. Согласно (6.1) касательное напряжение в турбулентном потоке:
|
|
|
|
|
|
|
|
2 |
||
|
du |
x |
|
du |
x |
|||||
t = m × |
|
|
+ r × l |
2 × |
|
|
. |
|||
dz |
dz |
|||||||||
|
|
|
|
|||||||
Если поток сильно турбулизирован, то первый член пренебрежимо
мал и тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
|
|
du |
x |
||||
t = tтурб |
= r × l |
2 × |
|
|
. |
||
dz |
|||||||
|
|
|
|
||||
Для вывода закона распределения скоростей при турбулентном дви- жении сначала введем предположения относительно длины пути переме- шивания l. Для определения длины пути перемешивания существует не- сколько формул, наиболее простой из них является формула Прандтля, со- гласно которой в безграничном потоке, движущемся вдоль плоской твер- дой стенки, l = c × z , где χ – коэффициент.
Измерения показывают, что вблизи стенки трубы при δв < z < @ 0,1 r0 можно принять l = 0,4 z, где δв – толщина вязкого подслоя. Однако при удалении от стенки эта зависимость становится не соответствующей дан- ным измерений и должна быть уточнена.
Примем l по формуле А.А. Саткевича для трубы: |
|
|
||||
l = c × z |
|
. |
|
|
|
|
1 - z r0 |
(7.12) |
|||||
Согласно (7.12) l приобретает наибольшее значение при z = |
2 |
r |
|
, а на |
||
|
|
|||||
3 0 |
|
|||||
стенке и на оси трубы длина пути перемешивания l=0.
Численные значения коэффициента χ зависят от числа Re, коэффици- ент χ изменяется при переходе от одних точек к другим в пределах живого сечения. Если поток взвесенесущий или аэрированный, то χ зависит от концентрации твердых частиц или воздуха в жидкости: с увеличением концентрации наносов и воздуха χ уменьшается.
140
Для турбулентных потоков в трубах χ приближенно можно принять равным 0,4. Это значение получено Никурадзе по данным опытов при тур- булентном режиме движения в круглых цилиндрических трубах с искусст- венно созданной равнозернистой шероховатостью. Для зоны живого сече- ния, в которой можно вследствие интенсивного перемешивания пренеб- речь чисто вязкостными напряжениями, то есть в турбулентном ядре, χ можно принимать по:
|
|
du 2 |
||
tтурб |
= r × l |
2 × |
|
|
|
||||
|
|
dz |
||
Здесь и далее обозначаем ux = u .
Подставив в эту формулу значение l из (7.12), получим:
|
|
|
z |
|
du 2 |
||
tтурб |
= rc2 z2 × 1 |
- |
|
|
× |
|
. |
|
|
||||||
|
|
|
r0 |
dz |
|||
Так как по (7.5) τ = τ0 (1 − z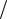 r0 ) , то:
r0 ) , то:
|
|
|
t0турб |
= rc2 z |
2 × |
du |
2 . |
|
|
|
|
||||
|
|
|
|
|
dz |
||
Но t |
0 |
r = u2 |
, и тогда: |
|
|
|
|
|
* |
|
|
|
|
|
|
du = u* × dz . c z
Здесь можно принять χ не зависящим от местоположения рассматри- ваемой точки по отношению к стенке трубы, то есть от z. Тогда, вынеся u* 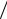 χ за знак интеграла, получим:
χ за знак интеграла, получим:
u = uc* × ln z + const ,
то есть логарифмический закон распределения скоростей в турбулентном
потоке.
Отметим, что хотя измерение длины пути перемешивания l нельзя осуществить, можно сопоставить измеренные в опыте значения скоростей (это легко сделать) с вычисленными по формуле распределения скоростей. Их полное или удовлетворительное совпадение будет свидетельствовать о правильности принятой формулы для l как функции z (то есть в зависимо- сти от удаления от стенки).
Логарифмический закон распределения скоростей вполне удовлетво- рительно согласуется с экспериментальными данными для труб и откры- тых потоков, за исключением области вблизи стенок, так как в пристенной области нельзя пренебречь вязкостными напряжениями.
141
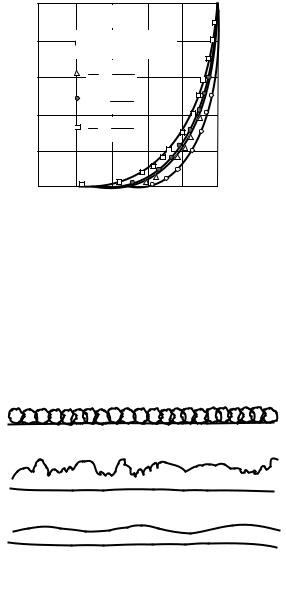
1,0 |
Re=106 |
|
|
|
||
z/r0 |
|
|
|
|||
0,8 |
|
гладкая |
|
|
||
поверхность |
|
|
||||
|
|
|
||||
0,6 |
|
= |
1 |
|
|
|
d |
252 |
|
|
|
||
|
|
|
|
|||
|
|
= |
1 |
|
|
|
0,4 |
d |
1014 |
|
|
|
|
|
|
|
|
|||
|
= |
1 |
|
|
|
|
|
|
|
|
|
||
|
d |
61 , 2 |
|
|
|
|
|
|
|
|
|
||
0,2 |
|
|
|
|
|
|
0 |
0,2 |
0,4 |
0,6 |
0,8 |
u/umax |
|
Рис. 7.7. Распределение |
|
|||||
осредненных скоростей в трубе |
||||||
при турбулентном движении |
||||||
При турбулентном движении пере- мешивание частиц жидкости и происходя- щий при этом обмен количеством движе- ния приводят к выравниванию осреднен- ных скоростей в различных точках живого сечения. Особенно это заметно при сравне- нии распределения осредненных скоростей в трубе при ламинарном (рис. 7.6) и турбу- лентном (рис. 7.7) движении. При лами- нарном движении υ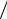 umax = 0,5 , а при тур- булентном движении это отношение – пе- ременное и увеличивается с увеличением числа Рейнольдса.
umax = 0,5 , а при тур- булентном движении это отношение – пе- ременное и увеличивается с увеличением числа Рейнольдса.
3.4. Шероховатость. Гидравлически гладкие и шероховаты тру- бы. Толщина вязкого подслоя
Шероховатость поверхности
труб может быть весьма различной. Если поверхность труб покрывается специально отсортированными зер-
нами песка одной фракции, то полу-
чается равнозернистая шерохова-
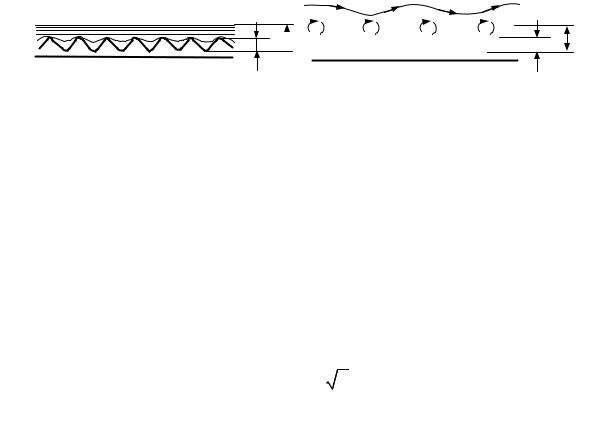
тость (рис. 7.8, а). Она используется только в лабораторных исследовани-
ях.
Поверхность труб обычно неравнозернистая, она может быть волни- стой с различными высотами и длинами волн (или микроволн) (рис. 7.8, б,
в).
Шероховатость стенок труб определяется рядом факторов: материа- лом стенок, характером механической обработки внутренней поверхности трубы, от чего зависят высота выступов шероховатости, их форма, густота и характер их размещения на поверхности; наличием или отсутствием в трубе ржавчины, коррозии, отложения осадков, защитных покрытий и т.д.
Для грубой количественной оценки шероховатости вводится понятие о средней высоте выступов (бугорков) шероховатости. Эту высоту, изме- ряемую в линейных единицах, называют абсолютной шероховатостью . Опыты показали, что при одной и той же величине абсолютной шерохова-
142
тости влияние ее на величину гидравлических сопротивлений и распреде- ление скоростей различно в зависимости от диаметра трубы. Поэтому вво- дится понятие об относительной шероховатости, измеряемой отношени- ем абсолютной шероховатости к диаметру трубы, то есть величиной D / d.
Учет конкретных особенностей шероховатости необходим в гидрав- лических исследованиях и расчетах.
Наиболее полные сведения о шероховатости, о размерах выступов и их взаимном расположении дает статистическое описание.
Понятие о гидравлически гладких и гидравлически шерохова-
тых трубах. Соотношение между высотой выступов шероховатости D и толщиной вязкого подслоя dв определяет структуру потока.
Если высота выступов шероховатости D меньше, чем толщина вязко- го подслоя dв, то все неровности полностью погружены в этот подслой и жидкость в пределах этого подслоя плавно обтекает выступы шероховато- сти. В этом случае шероховатость стенок не влияет на характер движения и, соответственно, потери напора не зависят от шероховатости. Такие стен- ки и трубы условно называются гидравлически гладкими (рис. 7.9, а).
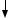 δв
δв 
 δв
δв
Если высота выступов шероховатости D превышает толщину вязкого подслоя dв, то неровности стенок выходят в пределы турбулентного ядра, поток обтекает выступы с отрывом, сопровождающимся интенсивным пе- ремешиванием частиц. В этом случае потери напора зависят от шероховато- сти, и такие трубы называются гидравлически шероховатыми (рис. 7.9, б). В третьем случае, являющемся промежуточным между двумя вышеуказан- ными, абсолютная высота выступов шероховатости примерно равна тол- щине вязкого подслоя.
Толщина вязкого подслоя определяется как:
dв |
» |
30 × d |
|
. |
(7.13) |
|
|
|
|
||||
|
|
Re × l |
|
|||
Таким образом, с ростом числа Re, а также коэффициента Дарси l, толщина вязкого подслоя dв уменьшается.
143
Разделение стенок (трубы) на гидравлически гладкие и шероховатые является условным, поскольку, как следует из формулы (7.13), толщина δв обратно пропорциональна числу Re. Таким образом, при движении жидко- сти вдоль одной и той же поверхности с неизменной высотой выступа ше- роховатости в зависимости от числа Рейнольдса толщина вязкого подслоя может изменяться. При увеличении числа Re толщина δв уменьшается и стенка, бывшая гидравлически гладкой, может стать шероховатой, так как высота выступов шероховатости окажется больше толщины вязкого под- слоя и шероховатость станет влиять на характер движения, и, следователь- но, на потери напора.
3.5. Экспериментальное изучение коэффициента Дарси. График
Никурадзе
Важные экспериментальные исследования, посвященные изучению зависимости коэффициента Дарси λ от числа Re и относительной шерохо- ватости, были проведены Никурадзе для шероховатых труб. Стенки труб и имели специально созданную равнозернистую шероховатость. Для созда- ния этой шероховатости сначала через калиброванные отверстия отсеивал- ся песок определенных размеров, который затем равномерно наносился на стенки, предварительно покрытые слоем лака, благодаря чему песок при- клеивался к стенкам. Размеры зерен песка принимались за размер выступа шероховатости . В результате были получены трубы с различными значе- ниями относительной шероховатости стенок: / d для труб (или относи- тельной гладкости d / как показано на рис. 7.10). В опытах были измере- ны потери напора и расход, вычислены средние скорости потоков и коэф- фициенты λ. Результаты Никурадзе показаны на рис. 7.10. По оси абсцисс отложены значения lg Re и по оси ординат lg (100λ). Представление опытных данных в таких координатах позволяет по углу наклона прямых (в частно- сти, I и II) получить показатель степени в степенной зависимости λ от Re.
Все опытные точки, полученные Никурадзе, до lgRe = 3,35 (Re < 2300, ламинарный режим движения) независимо от шероховатости стенок труб располагаются на прямой. Это значит, что при ламинарном движении λ не зависит от шероховатости трубы . При Re 2300 ÷ 3000 (lg Re = 3,35 ÷ 3,5) происходит переход от ламинарного режима к турбулентному. В опытах Никурадзе в пределах 2300 < Re < 4000 коэффициент λ по-прежнему не за- висит от шероховатости. При турбулентном движении Re > 4000 характер
144
экспериментальных кривых различен в зависимости от значения d / D. При больших относительных шероховатостях (d / D = 30) экспериментальная
кривая сначала продолжает подниматься, а затем при Rе = 3 ×104 становит- ся горизонтальной. При меньших относительных шероховатостях кривые ведут себя иначе: сначала независимо от относительной шероховатости экспериментальные точки ложатся на прямую II. Затем по достижении Rе ³ 20 d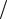 D эти точки на графике рис. 7.10 отходят от прямой II, образуют
D эти точки на графике рис. 7.10 отходят от прямой II, образуют
впадину, и при Re ³ 500 d / D превращаются в горизонтальные прямые.
Таким образом, исследования, выполненные Никурадзе, наглядно свидетельствуют о наличии различных областей сопротивления при на- порном движении в трубах:
1-я область – ламинарный режим движения (Re £ 2300) l = f (Re–1 ), прямая I на рис. 7.10:
l = 64 (формула Пуазейля);
Re
2-я область – переход от ламинарного к турбулентному режиму
2300 £ Re £ 4000;
3-я область – турбулентный режим, гидравлически гладкие трубы, λ =f (Re–0,25 ), пряма II на рис. 7.10:
145
