Экспоненциальный закон распределения.
Листинг программы для реализации СВ с помощью встроенной функции матлаб:
clear all
lambda=2;
m=1/lambda;
N=1000;
%ПО ВСТРОЕННОЙ ФУНКЦИИ
Y_vstr = exprnd(m, N, 1);
figure(1)
plot(Y_vstr)
xlabel('Номер элемента в выборке')
ylabel('Значения СВ')
grid on
Результаты работы программы:
Рисунок 112 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000
Листинг программы для реализации СВ с помощью формулы:
%ПО ФОРМУЛЕ
a1=rand(1,N); % сгенерировать a1 размерностью N
Y_form=log(a1)/(-lambda);
figure(2)
plot(Y_form)
xlabel('Номер элемента в выборке')
ylabel('Значения СВ')
grid on
Результаты работы программы:
Рисунок 13 - График распределения СВ, построенный с помощью формулы, при N=1000
Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000
figure(4)
histfit(Y_form, 50, 'exponential')
grid on
xlabel("Значение");
ylabel("Вероятность");
m_y = mean (Y_form) % вычисление мат. ожидания
st_y = std (Y_form) % вычисление СКО
sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии
kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса
Результаты работы программы:
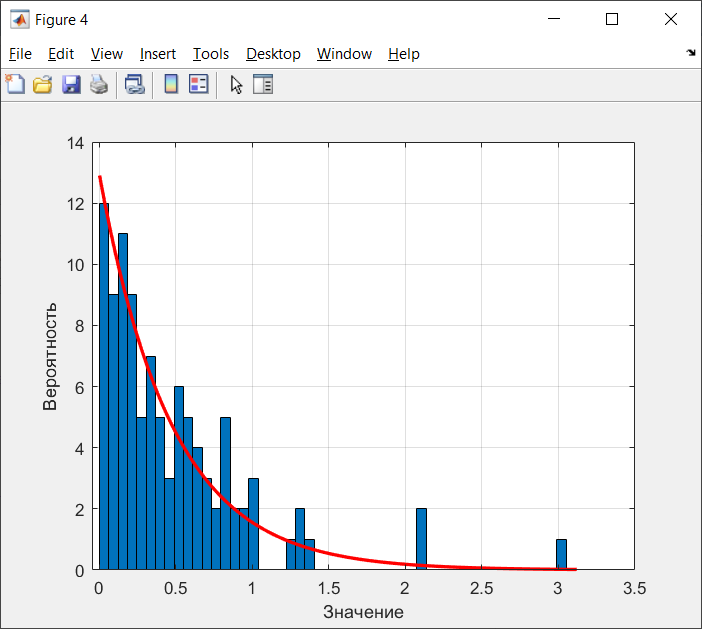
Рисунок 14 - Гистограмма экспоненциального распределения СВ, при N=100
Вычисленные значения, при N=100:
Математическое ожидание: 0.4721
Дисперсия: 0.2330
СКО: 0.4827
Коэффициент асимметрии: 2.3511
Коэффициент эксцесса: 7.9122
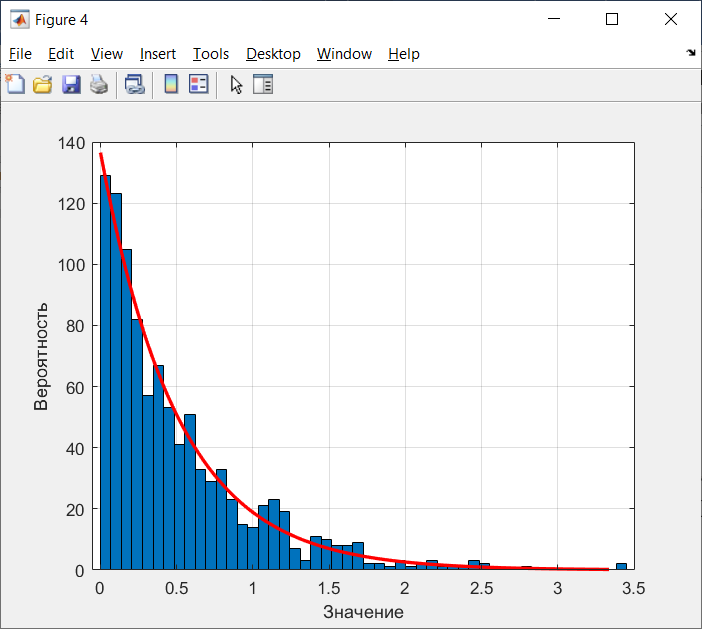
Рисунок 22 - Гистограмма экспоненциального распределения СВ, при N=1000
Вычисленные значения, при N=1000:
Математическое ожидание: 0.5046
Дисперсия: 0.2509
СКО: 0.5009
Коэффициент асимметрии: 1.7808
Коэффициент эксцесса: 4.1622
Рисунок 23 - Гистограмма экспоненциального распределения СВ, при N=10000
Вычисленные значения, при N=10000:
Математическое ожидание: 0.5044
Дисперсия: 0.2524
СКО: 0.5024
Коэффициент асимметрии: 1.9781
Коэффициент эксцесса: 5.9436
Рэлея закон распределения.
Листинг программы для реализации СВ с помощью встроенной функции матлаб:
clear all
m=10;
sigma = sqrt(m);
N=1000;
%ПО ВСТРОЕННОЙ ФУНКЦИИ
Y_vstr = raylrnd(sigma, N, 1);
figure(1)
plot(Y_vstr)
xlabel('Номер элемента в выборке')
ylabel('Значения СВ')
grid on
figure(2)
hist(Y_vstr)
grid on
xlabel("Значение");
ylabel("Частота");
axis([0 20 0 300]);
Результаты работы программы:
Рисунок 24 - График распределения СВ, построенный по встроенной функции MATLAB, при N=1000
Листинг программы для реализации СВ с помощью формулы:
%ПО ФОРМУЛЕ
a1=rand(1,N); % сгенерировать a1 размерностью N
Y_form=sigma*sqrt(-2*log(a1));
figure(3)
plot(Y_form)
xlabel('Номер элемента в выборке')
ylabel('Значения СВ')
grid on
Результаты работы программы:
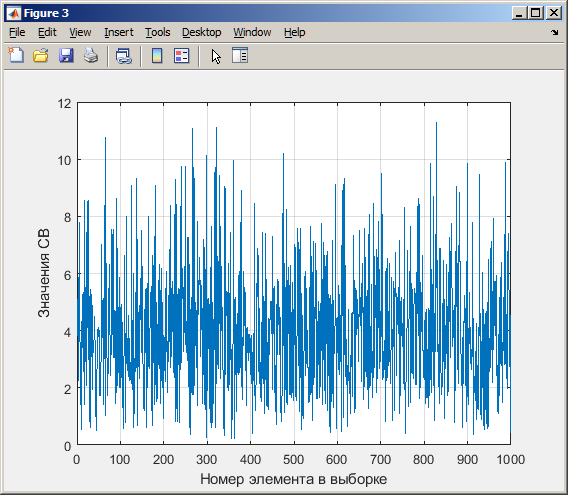
Рисунок 25 - График распределения СВ, построенный с помощью формулы, при N=1000
Анализ и сравнение результатов и построение гистограмм, при N=100, 1000 и 10000
figure(4)
histfit(Y_form, 50, 'rayleigh')
grid on
xlabel("Значение");
ylabel("Вероятность");
m_y = mean (Y_form) % вычисление мат. ожидания
d_y = var(Y_form) % вычисление дисперсии
st_y = std (Y_form) % вычисление СКО
sk_Y = skewness(Y_form) % вычисление коэффициента асимметрии
kur_Y = kurtosis(Y_form)-3 % вычисление коэффициента эксцесса
Результаты работы программы:
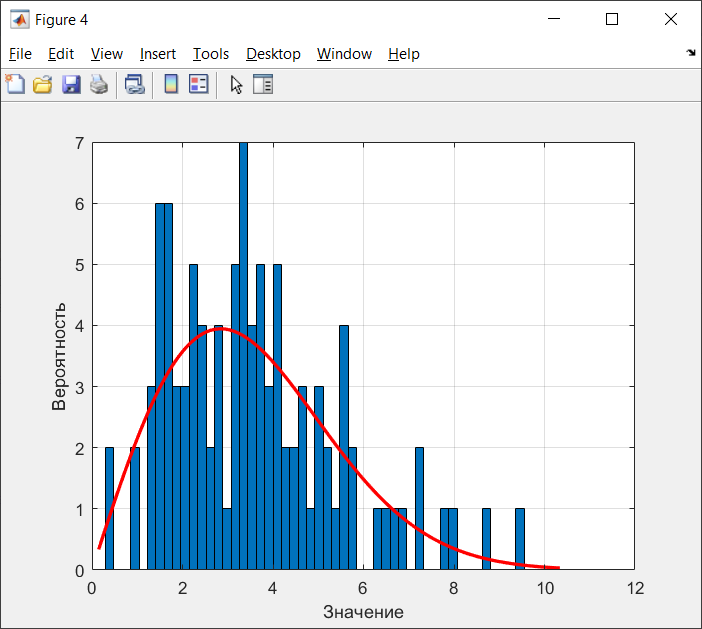
Рисунок 26 - Гистограмма Рэлей распределения СВ, при N=100
Вычисленные значения, при N=100:
Математическое ожидание: 3.5661
Дисперсия: 3.4963
СКО: 1.8698
Коэффициент асимметрии: 0.8352
Коэффициент эксцесса: 0.5363
Рисунок 27 - Гистограмма Рэлей распределения СВ, при N=1000
Вычисленные значения, при N=1000:
Математическое ожидание: 4.1366
Дисперсия: 4.2540
СКО: 2.0625
Коэффициент асимметрии: 0.6203
Коэффициент эксцесса: 0.3559
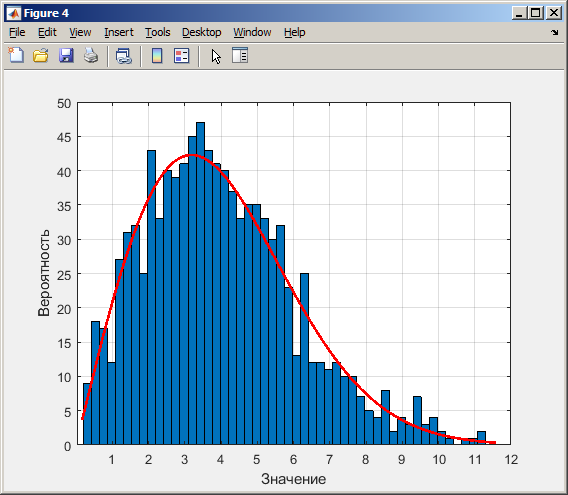
Рисунок 28 - Гистограмма Рэлей распределения СВ, при N=10000
Вычисленные значения, при N=10000:
Математическое ожидание: 3.9658
Дисперсия: 4.3892
СКО: 2.0950
Коэффициент асимметрии: 0.6413
Коэффициент эксцесса: 0.2731